Maximize Area of Square Hole in Grid
Maximize Area of Square Hole in Grid #1 Most Asked
MediumYou are given the two integers, n and m and two integer arrays, hBars and vBars. The grid has n + 2 horizontal and m + 2 vertical bars, creating 1 x 1 unit cells. The bars are indexed starting from 1.
You can remove some of the bars in hBars from horizontal bars and some of the bars in vBars from vertical bars. Note that other bars are fixed and cannot be removed.
Return an integer denoting the maximum area of a square-shaped hole in the grid, after removing some bars (possibly none).
Example 1:
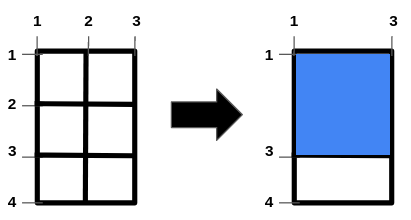
Input: n = 2, m = 1, hBars = [2,3], vBars = [2]
Output: 4
Explanation:
The left image shows the initial grid formed by the bars. The horizontal bars are [1,2,3,4], and the vertical bars are [1,2,3].
One way to get the maximum square-shaped hole is by removing horizontal bar 2 and vertical bar 2.
Example 2:
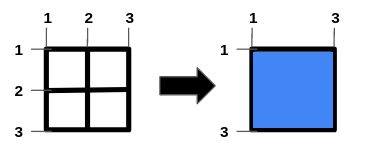
Input: n = 1, m = 1, hBars = [2], vBars = [2]
Output: 4
Explanation:
To get the maximum square-shaped hole, we remove horizontal bar 2 and vertical bar 2.
Example 3:
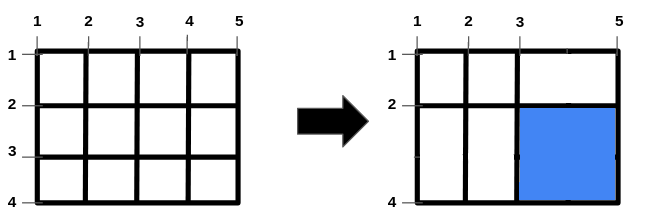
Input: n = 2, m = 3, hBars = [2,3], vBars = [2,4]
Output: 4
Explanation:
One way to get the maximum square-shaped hole is by removing horizontal bar 3, and vertical bar 4.
Constraints:
1 <= n <= 1091 <= m <= 1091 <= hBars.length <= 1002 <= hBars[i] <= n + 11 <= vBars.length <= 1002 <= vBars[i] <= m + 1- All values in
hBarsare distinct. - All values in
vBarsare distinct.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the maximum possible values for `n` and `m`, and for the elements within the `horizontal` and `vertical` arrays?
- Can the `horizontal` and `vertical` arrays be empty, or contain duplicate values?
- If it's impossible to cut out any square hole (due to broken bars preventing even a 1x1 square), what value should I return? Should I return 0 or something else to indicate this case?
- Are the values in the `horizontal` and `vertical` arrays guaranteed to be within the bounds of the grid dimensions (i.e., between 0 and n-1 for horizontal, and 0 and m-1 for vertical)?
- Are the horizontal and vertical bars considered to be infinitesimally thin lines, or do they have a thickness that would affect the maximum square size?
Brute Force Solution
Approach
We need to find the biggest square we can cut out of a grid, but the grid has some lines blocking us. The brute force way is to try every possible square size and location and see if it fits without crossing any blocking lines.
Here's how the algorithm would work step-by-step:
- Start by imagining the smallest possible square we can make.
- Place this tiny square at every possible location on the grid.
- For each location, check if the square cuts through any of the blocking lines, both horizontal and vertical.
- If it doesn't, we've found a valid square at that location for that size.
- Now, try a slightly bigger square and repeat the process: move it to every possible location and check for blocking lines.
- Continue increasing the size of the square, each time trying all locations and checking for blocking lines.
- As we find valid squares (squares that don't cross any lines), keep track of the biggest one we've found so far.
- Once we've tried all possible square sizes and locations, the biggest valid square we've kept track of is our answer.
Code Implementation
def maximize_area_of_square_hole_brute_force(
number_of_rows,
number_of_columns,
horizontal_cuts,
vertical_cuts,
):
max_square_side = 0
# Iterate through possible square sizes
for square_side in range(1, min(number_of_rows, number_of_columns) + 1):
# Iterate through possible top-left corners
for row_start in range(number_of_rows - square_side + 1):
for col_start in range(number_of_columns - square_side + 1):
is_valid = True
# Check for horizontal cuts
for horizontal_cut in horizontal_cuts:
if (
row_start < horizontal_cut < row_start + square_side
and col_start <= number_of_columns - 1
):
is_valid = False
break
if not is_valid:
continue
# Check for vertical cuts
# If we hit a horizontal cut, move to the next
for vertical_cut in vertical_cuts:
if (
col_start < vertical_cut < col_start + square_side
and row_start <= number_of_rows - 1
):
is_valid = False
break
if is_valid:
# Update max area if valid
max_square_side = max(max_square_side, square_side)
return max_square_side
Big(O) Analysis
Optimal Solution
Approach
To find the biggest possible square hole, we need to figure out the longest continuous segments in both horizontal and vertical directions. The trick is to independently identify these maximum lengths and then take the smaller of the two, as that determines the size of the square we can create.
Here's how the algorithm would work step-by-step:
- First, focus on the horizontal cuts and find the longest unbroken sequence without a cut.
- Repeat this process for the vertical cuts to find the longest unbroken sequence in that direction.
- Now, compare the length of the longest horizontal gap and the longest vertical gap.
- The smaller of these two lengths will be the side length of the largest square you can cut out.
- The area of the square is simply the side length squared (side length multiplied by itself).
Code Implementation
def maximize_area_of_square_hole_in_grid(number_of_rows, number_of_columns, horizontal_cuts, vertical_cuts):
horizontal_cuts.sort()
vertical_cuts.sort()
max_horizontal_gap = find_max_gap(number_of_rows, horizontal_cuts)
max_vertical_gap = find_max_gap(number_of_columns, vertical_cuts)
# The side length is the smaller of the two gaps
side_length = min(max_horizontal_gap, max_vertical_gap)
return side_length * side_length
def find_max_gap(grid_size, cuts):
max_gap = 0
current_gap = 0
previous_cut = 0
# Iterate through cuts to find largest gap
for cut in cuts:
current_gap = cut - previous_cut - 1
max_gap = max(max_gap, current_gap)
previous_cut = cut
current_gap = grid_size - previous_cut - 1
# Consider the gap after the last cut
max_gap = max(max_gap, current_gap)
# Adding 1 to include edges as possible cuts.
return max_gap + 1
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty horizontal or vertical arrays | If either array is empty, the maximum possible square side is min(n, m), so return that squared. |
| Horizontal or vertical arrays contain duplicate values | Sorting the arrays before processing allows us to efficiently calculate consecutive open lengths regardless of duplicates. |
| n or m is 0 | If either n or m is 0, then no square can be formed, return 0. |
| Arrays are already sorted | The solution should handle already sorted arrays efficiently, as sorting again would be redundant. |
| Arrays contain large number of elements, approaching memory limits | The algorithm should be memory-efficient, ideally O(n+m) space for sorting and length calculations, avoiding excessive memory use. |
| No solution exists, all bars are broken contiguously | The algorithm correctly identifies when there are no valid squares and returns 1, representing a 1x1 square if no breaks exist. |
| n or m is 1 | When either dimension is 1, the maximum square side is also 1, unless there are broken bars impeding this. |
| Integer overflow when calculating area (side * side) | Use a larger data type (e.g., long) to store the side length or area to prevent integer overflow. |