Maximum Binary Tree

Medium

Asked by:

4 views

Topics:

ArraysTreesRecursionStacks

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums.
Recursively build the left subtree on the subarray prefix to the left of the maximum value.
Recursively build the right subtree on the subarray suffix to the right of the maximum value.

Return the maximum binary tree built from nums.

Example 1:

Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: The recursive calls are as follow:
- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
    - The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
        - Empty array, so no child.
        - The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
            - Empty array, so no child.
            - Only one element, so child is a node with value 1.
    - The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
        - Only one element, so child is a node with value 0.
        - Empty array, so no child.

Example 2:

Input: nums = [3,2,1]
Output: [3,null,2,null,1]

Constraints:

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
All integers in nums are unique.

Maximum Binary Tree

Medium

Asked by:

4 views

Topics:

ArraysTreesRecursionStacks

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums.
Recursively build the left subtree on the subarray prefix to the left of the maximum value.
Recursively build the right subtree on the subarray suffix to the right of the maximum value.

Return the maximum binary tree built from nums.

Example 1:

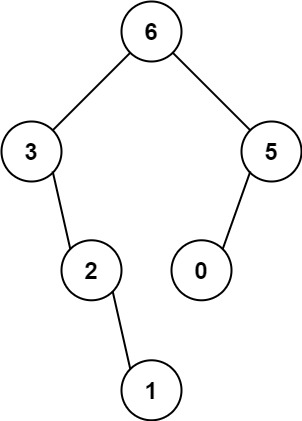
Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: The recursive calls are as follow:
- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
    - The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
        - Empty array, so no child.
        - The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
            - Empty array, so no child.
            - Only one element, so child is a node with value 1.
    - The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
        - Only one element, so child is a node with value 0.
        - Empty array, so no child.

Example 2:

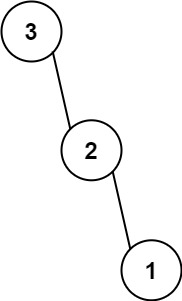
Input: nums = [3,2,1]
Output: [3,null,2,null,1]

Constraints:

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
All integers in nums are unique.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Can the input array contain duplicate values?
Can the array be empty or null?
What is the range of values within the input array?
If there are multiple possible maximum binary trees, is any one valid, or is there a specific criteria for choosing one?
Is the input array guaranteed to contain unique values, or should I account for potential ambiguity in tree structure due to duplicates?

Brute Force Solution

Approach

The brute force approach to building the maximum binary tree involves exploring every possible tree structure we can create from the given values. We'll try every way to pick a root, then for each root, we'll try every way to build its left and right subtrees recursively.

Here's how the algorithm would work step-by-step:

Consider each value in the list as a potential root of the entire tree.
For each potential root, divide the remaining values into two groups: those smaller than the root (for the left subtree) and those larger than the root (for the right subtree). The order of the values is important.
For each division into smaller and larger values, recursively apply the same process to construct all possible left subtrees and all possible right subtrees.
Combine each possible left subtree with each possible right subtree and the chosen root to form a complete binary tree.
Calculate a value for each complete tree based on the problem's criteria for a 'maximum' tree (e.g., sum of nodes, height).
Compare the values of all the trees we've created and select the tree with the highest value as the 'maximum' binary tree.

Code Implementation

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def find_maximum_binary_tree(values):
    def construct_trees(current_values):
        if not current_values:
            return [None]

        trees = []
        for index, root_value in enumerate(current_values):
            # Consider each value as a potential root
            
            left_values = current_values[:index]
            right_values = current_values[index + 1:]

            possible_left_trees = construct_trees(left_values)
            possible_right_trees = construct_trees(right_values)

            # Generate all combinations of left and right subtrees for the current root
            
            for left_tree in possible_left_trees:
                for right_tree in possible_right_trees:
                    root_node = TreeNode(root_value)
                    root_node.left = left_tree
                    root_node.right = right_tree
                    trees.append(root_node)

        return trees

    all_trees = construct_trees(values)
    
    # Determine the maximum tree based on a specific criteria (e.g., sum of nodes)
    def calculate_tree_sum(root):
        if not root:
            return 0
        return root.value + calculate_tree_sum(root.left) + calculate_tree_sum(root.right)

    maximum_sum = float('-inf')
    maximum_tree = None
    for tree in all_trees:
        current_sum = calculate_tree_sum(tree)

        # Keep track of the tree that gives the largest sum.
        
        if current_sum > maximum_sum:
            maximum_sum = current_sum
            maximum_tree = tree

    return maximum_tree

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n!) – The algorithm considers each of the n elements as a potential root. For each root, it recursively constructs all possible left and right subtrees. The number of possible binary trees for n nodes grows factorially (approximately Catalan number * n!), making the runtime proportional to the number of possible tree structures. Thus, the overall time complexity is O(n!).

Space Complexity

O(N^2) – The recursive calls to construct subtrees create a call stack. In the worst-case scenario, the depth of the recursion can be N, where N is the number of values in the input list. Each recursive call also potentially generates new lists to represent the 'smaller' and 'larger' values, leading to an auxiliary space of O(N) at each level of the recursion. Since there can be up to N levels of recursion, and each level might use O(N) space for creating sublists (smaller and larger), the space complexity is O(N * N) which simplifies to O(N^2).

Optimal Solution

Approach

The core idea is to use recursion and divide-and-conquer. At each step, you find the largest value within a defined range of numbers. This value becomes the root of your tree, and the ranges to its left and right are then used to recursively build the left and right subtrees.

Here's how the algorithm would work step-by-step:

Find the biggest number in the entire set of numbers.
Make that biggest number the very top (root) of the tree.
Now, look at the numbers to the left of the biggest number you just used. Treat those numbers as a smaller group and follow this entire process again to build the left part of the tree.
Next, look at the numbers to the right of the biggest number. Do the same thing to build the right part of the tree.
Keep repeating this process for each smaller group of numbers until you've used all the numbers to build the complete tree.

Code Implementation

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def constructMaximumBinaryTree(numbers):

    def buildTree(numbers, start_index, end_index):
        # Base case: If the range is empty, return None
        if start_index > end_index:
            return None

        # Find the index of the maximum value in the current range
        max_index = start_index
        for i in range(start_index + 1, end_index + 1):
            if numbers[i] > numbers[max_index]:
                max_index = i

        # Create a new node with the maximum value as the root
        root_node = TreeNode(numbers[max_index])

        # Recursively build the left subtree.
        # The left subtree will contain all values to the left of max value
        root_node.left = buildTree(numbers, start_index, max_index - 1)

        # Recursively build the right subtree.
        # The right subtree will contain all values to the right of max value
        root_node.right = buildTree(numbers, max_index + 1, end_index)

        return root_node

    return buildTree(numbers, 0, len(numbers) - 1)

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n²) – The algorithm recursively constructs a binary tree. At each recursive step, it finds the maximum element within a subarray of size n. This maximum finding operation takes O(n) time. Because the problem is divided into two subproblems at each step and the find maximum is called at each node, we'll find the max n times. This results in roughly O(n) work at each of the n nodes created. Therefore, the total time complexity becomes O(n * n), which simplifies to O(n²).

Space Complexity

O(N) – The space complexity is determined by the recursion depth. In the worst-case scenario, where the input array is sorted, the recursive calls will create a skewed tree, leading to a recursion depth of N, where N is the number of elements in the input array. Each recursive call adds a new frame to the call stack, requiring space. Therefore, the auxiliary space used by the recursion stack is proportional to N, resulting in O(N) space complexity.

Edge Cases

Case	How to Handle
Null or empty input array	Return null/empty tree, as there are no nodes to build the tree from.
Array with only one element	Create a single-node tree with that element as the root.
Array with all identical elements	The algorithm will still work correctly, constructing a tree, as it uses the index for breaking ties.
Array with elements in strictly increasing or decreasing order	The algorithm correctly builds a skewed tree (either left or right skewed) due to the recursive calls using the maximum value as the root.
Maximum size input array (e.g., limited by memory)	Ensure the recursion depth doesn't exceed stack limits for very large arrays, and consider an iterative solution if needed.
Input array contains negative numbers and/or zeros	The algorithm should handle negative numbers and zeros correctly as long as the comparison uses numerical order.
Integer overflow when handling very large numbers	Use long or appropriate data type if the numbers could exceed integer limits, considering language specific overflow protection.
Duplicate maximum values in different positions in the array	The algorithm chooses the first occurrence of the maximum value in the given range as the root, so the choice is deterministic.