Maximum Depth of Binary Tree #10 Most Asked
EasyGiven the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example 1:
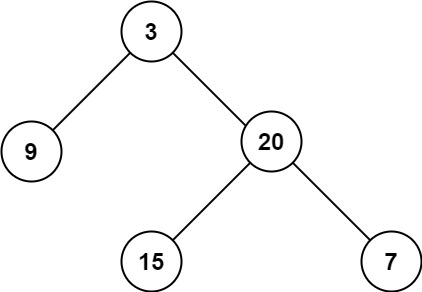
Input: root = [3,9,20,null,null,15,7] Output: 3
Example 2:
Input: root = [1,null,2] Output: 2
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -100 <= Node.val <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the data type of the node values in the binary tree, and are there any restrictions on the values (e.g., negative numbers, duplicates)?
- Can the tree be empty (root is null), and if so, what should the function return in that case?
- Is the tree guaranteed to be a valid binary tree, or should I handle cases where the structure is malformed (e.g., cycles, multiple roots)?
- Could you provide an example of a tree with a depth greater than 2, just to clarify the expected output for a slightly more complex scenario?
- Are we considering only complete paths from root to leaf, or could a path end at any node?
Brute Force Solution
Approach
Finding the maximum depth of a tree is like exploring a maze. The brute force approach involves trying every possible path from the entrance to a dead end to see how far you can go. We explore each route fully before considering other routes, making sure we check everything.
Here's how the algorithm would work step-by-step:
- Start at the very beginning, the top of the tree.
- Go down one path, all the way to the end, counting how many steps you took.
- Go back to the beginning, and try another path all the way to its end, again counting the steps.
- Do this for absolutely every single path in the tree, making sure you get to the end of each one.
- Keep track of the longest path you found during your exploration.
- Once you've tried absolutely every path, the longest one you found is the answer.
Code Implementation
def max_depth_brute_force(root):
if not root:
return 0
maximum_depth = 0
def calculate_depth(node, current_depth):
nonlocal maximum_depth
# If we've reached a leaf node, update the maximum depth.
if not node.left and not node.right:
maximum_depth = max(maximum_depth, current_depth)
return
# Explore the left subtree.
if node.left:
calculate_depth(node.left, current_depth + 1)
# Explore the right subtree.
if node.right:
calculate_depth(node.right, current_depth + 1)
calculate_depth(root, 1)
return maximum_depthBig(O) Analysis
Optimal Solution
Approach
The best way to find the maximum depth is to explore the tree level by level. We essentially ask each part of the tree: What's the deepest you go? We then combine those answers to find the overall deepest point.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, which is called the root.
- Ask the root node, what's the deepest you can go from here?
- The root node asks the same question to its left and right children (the nodes directly below it).
- Each child node recursively asks the same question to its children, and so on, until we reach the very bottom of the tree (the leaves).
- When we get to a leaf, which has no children, the answer to the question 'What's the deepest you can go?' is just 1 (because it's just the leaf itself).
- Each parent node then receives the answers from its left and right children.
- The parent node takes the bigger of the two answers it received, adds 1 (to account for itself), and sends that number up to its own parent.
- This continues all the way up to the root node.
- Finally, the root node receives the answers from its children, takes the bigger one, adds 1, and that's the maximum depth of the whole tree!
Code Implementation
def max_depth(root):
if root is None:
return 0
# Recursively get the depth of the left subtree.
left_subtree_depth = max_depth(root.left)
# Recursively get the depth of the right subtree.
right_subtree_depth = max_depth(root.right)
# Choose the larger depth and increment for the current node.
return max(left_subtree_depth, right_subtree_depth) + 1
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree (root is null) | Return 0 if the root is null, as an empty tree has depth 0. |
| Tree with only a root node | Return 1 if the root is the only node, representing a depth of 1. |
| Completely unbalanced tree (left or right skewed) | The recursive or iterative depth-first approach will traverse the longest path correctly, handling skewness naturally. |
| Very deep tree (potential stack overflow with recursion) | Consider iterative solution (BFS or DFS with stack) to avoid stack overflow for extremely deep trees. |
| Tree with a very large number of nodes (memory constraints) | The solution's memory usage should scale linearly with the number of nodes visited at any given level for BFS, or depth for DFS; ensure no unnecessary memory allocation happens |
| Binary search tree structure with duplicate values | The depth calculation algorithm does not depend on the values of the nodes, therefore duplicates have no impact. |
| Negative or zero values in tree nodes. | The algorithm calculates the depth based on the tree structure and connections, and is not affected by node values themselves. |
| Integer overflow if tree is extremely deep on some architectures | Use a datatype that avoids potential integer overflow if the depth is expected to exceed typical integer limits (e.g., long). |