Maximum Employees to Be Invited to a Meeting
Maximum Employees to Be Invited to a Meeting #2 Most Asked
HardA company is organizing a meeting and has a list of n employees, waiting to be invited. They have arranged for a large circular table, capable of seating any number of employees.
The employees are numbered from 0 to n - 1. Each employee has a favorite person and they will attend the meeting only if they can sit next to their favorite person at the table. The favorite person of an employee is not themself.
Given a 0-indexed integer array favorite, where favorite[i] denotes the favorite person of the ith employee, return the maximum number of employees that can be invited to the meeting.
Example 1:
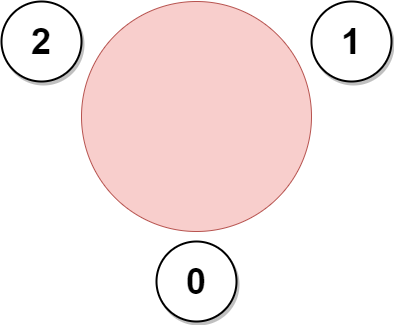
Input: favorite = [2,2,1,2] Output: 3 Explanation: The above figure shows how the company can invite employees 0, 1, and 2, and seat them at the round table. All employees cannot be invited because employee 2 cannot sit beside employees 0, 1, and 3, simultaneously. Note that the company can also invite employees 1, 2, and 3, and give them their desired seats. The maximum number of employees that can be invited to the meeting is 3.
Example 2:
Input: favorite = [1,2,0] Output: 3 Explanation: Each employee is the favorite person of at least one other employee, and the only way the company can invite them is if they invite every employee. The seating arrangement will be the same as that in the figure given in example 1: - Employee 0 will sit between employees 2 and 1. - Employee 1 will sit between employees 0 and 2. - Employee 2 will sit between employees 1 and 0. The maximum number of employees that can be invited to the meeting is 3.
Example 3:
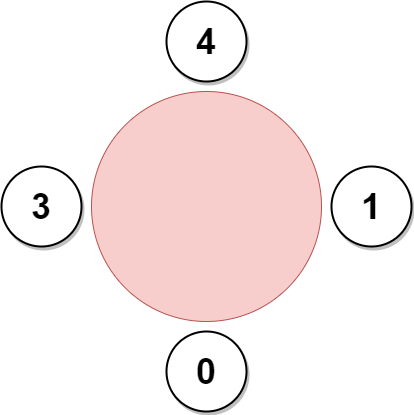
Input: favorite = [3,0,1,4,1] Output: 4 Explanation: The above figure shows how the company will invite employees 0, 1, 3, and 4, and seat them at the round table. Employee 2 cannot be invited because the two spots next to their favorite employee 1 are taken. So the company leaves them out of the meeting. The maximum number of employees that can be invited to the meeting is 4.
Constraints:
n == favorite.length2 <= n <= 1050 <= favorite[i] <= n - 1favorite[i] != i
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum number of employees (size of the 'favorite' array) we should expect?
- Can the 'favorite' array contain cycles of length greater than 2, or can we assume the cycles are either of length 1 (self-loop) or length 2?
- If there are no employees that can be invited to the meeting (e.g., empty 'favorite' array or no valid pairings), what should I return?
- Are the employee IDs zero-indexed or one-indexed?
- Could there be self-loops in the 'favorite' array, where favorite[i] == i?
Brute Force Solution
Approach
The brute force approach to this problem is to consider every possible group of employees that could attend the meeting. We will explore all the different combinations of attendees, from small groups to large groups. For each combination, we check if it is a valid group based on the given rules.
Here's how the algorithm would work step-by-step:
- Start by considering just one employee to be the attendee.
- Check if this single employee can attend according to the meeting rules (i.e., does that employee like themselves?).
- Next, consider all pairs of employees who could attend.
- For each pair, check if they both like each other, because if they don't, they can't both attend.
- Then, consider all groups of three employees, four employees, and so on, until we have considered all employees attending.
- For each group, we need to check that everyone in the group likes each other; if even one person doesn't like another in the group, this group is invalid.
- Keep track of the largest valid group of employees we find as we go.
- Once we have examined all possible groups, the size of the largest valid group is the answer.
Code Implementation
def maximum_employees_to_be_invited_to_a_meeting(favorite):
number_of_employees = len(favorite)
maximum_invited_employees = 0
for i in range(1 << number_of_employees):
group_of_employees = []
for j in range(number_of_employees):
if (i >> j) & 1:
group_of_employees.append(j)
is_valid_group = True
# Check if everyone likes each other
for employee_one in group_of_employees:
for employee_two in group_of_employees:
if employee_one == employee_two:
continue
if favorite[employee_one] != employee_two:
is_valid_group = False
break
if not is_valid_group:
break
# Update maximum if valid
if is_valid_group:
maximum_invited_employees = max(maximum_invited_employees, len(group_of_employees))
return maximum_invited_employeesBig(O) Analysis
Optimal Solution
Approach
This problem involves finding the largest possible group of employees to invite to a meeting given a preference system. We break this down into two main parts: finding the longest possible chains of mutual preferences, and finding the largest possible cycles of preferences, then combine the results.
Here's how the algorithm would work step-by-step:
- First, find the longest possible 'chains' of employees who mutually prefer each other. Since each employee has only one preference, we can trace these relationships like following a map.
- To find these chains, for each employee, we'll go as far as we can in both directions of their mutual preference. Count how many employees are in the longest possible path.
- Next, find 'cycles' of employees where each employee's preference leads back to themselves, forming a closed loop. Think of this like a group of people standing in a circle, each pointing to the next person.
- For each employee, check if their preference leads back to them through a series of preferences. If it does, note down all the employees involved in that cycle.
- To get the final answer, combine the results. Add up all the employees in the mutual-preference chains we found. Separately get the total number of employees in the largest cycle.
- Choose the largest between (1) the total employees in chains and (2) the total employees in the largest cycle, this is the maximum number of employees that can be invited. The main trick is recognizing you can split the problem into finding just these two kinds of groupings and taking the maximum of each.
Code Implementation
def maximum_invited_employees(preferences):
number_of_employees = len(preferences)
longest_chain_lengths = [0] * number_of_employees
visited = [False] * number_of_employees
def depth_first_search(employee_id):
if visited[employee_id]:
return 0
visited[employee_id] = True
preferred_employee = preferences[employee_id]
length = depth_first_search(preferred_employee)
visited[employee_id] = False
longest_chain_lengths[employee_id] = length + 1
return length + 1
# Calculate chain lengths for mutual preferences.
mutual_preference_sum = 0
for employee_id in range(number_of_employees):
if preferences[preferences[employee_id]] == employee_id:
longest_chain_lengths[employee_id] = 1
mutual_preference_sum += get_chain_length(employee_id, preferences, longest_chain_lengths)
def get_chain_length(employee_id, preferences, longest_chain_lengths):
if longest_chain_lengths[employee_id] != 1:
return 0
first_employee = employee_id
second_employee = preferences[employee_id]
chain_length_for_pair = 0
chain_length_for_pair = find_longest_path(first_employee, preferences,longest_chain_lengths)
return chain_length_for_pair
def find_longest_path(employee_id, preferences,longest_chain_lengths):
maximum_length = 0
#Traverse left from the node
maximum_length = max(maximum_length, 1 + find_chain_length(employee_id, preferences,longest_chain_lengths))
return maximum_length
def find_chain_length(employee_id, preferences,longest_chain_lengths):
chain_length = 0
longest_path_ending_here = [0] * number_of_employees
# Find longest chain that ends here
for i in range(number_of_employees):
if preferences[i] == employee_id and i != employee_id:
chain_length = max(chain_length,find_longest_path(i, preferences,longest_chain_lengths))
return chain_length
# Find the maximum cycle length.
maximum_cycle_length = 0
visited = [False] * number_of_employees
for employee_id in range(number_of_employees):
if not visited[employee_id]:
current_cycle_length = 0
current_employee = employee_id
path = []
while not visited[current_employee]:
visited[current_employee] = True
path.append(current_employee)
current_employee = preferences[current_employee]
#If employee is in the path, it is a cycle
if current_employee in path:
index = path.index(current_employee)
current_cycle_length = len(path) - index
maximum_cycle_length = max(maximum_cycle_length, current_cycle_length)
# Calculate the maximum invited employees.
return max(mutual_preference_sum // 2, maximum_cycle_length)Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty favorite list | Return 0 as no employees can be invited with an empty list. |
| Single employee in the list | Return 1 as a single employee can be invited to a 'meeting' with themself. |
| Favorite list contains self-loops (i.e., favorite[i] == i) | Handle this by ignoring self-loops during cycle detection and path finding to avoid infinite loops or incorrect calculations. |
| Very large number of employees (close to the maximum integer size) | Ensure data structures (e.g., arrays, lists) are adequately sized to avoid integer overflow or memory issues; be mindful of memory limitations. |
| Multiple disjoint cycles exist within the favorite list | The solution should correctly identify and process each disjoint cycle to maximize the number of invited employees from the longest possible cycles or paths. |
| No cycles exist, only mutual favorites and single paths | The algorithm should still correctly identify and include mutually liked pairs and the longest chain from each side of them to maximize invited employees. |
| All employees like the same person | The maximum number of invited employees should be 2, as they all form mutual pairs with the single employee who is liked. |
| List contains extremely long paths without cycles | Be mindful of potential stack overflow errors when using recursive approaches for path exploration, and consider iterative depth-first search or dynamic programming approaches instead. |