Maximum Number of Achievable Transfer Requests
HardWe have n buildings numbered from 0 to n - 1. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.
You are given an array requests where requests[i] = [fromi, toi] represents an employee's request to transfer from building fromi to building toi.
All buildings are full, so a list of requests is achievable only if for each building, the net change in employee transfers is zero. This means the number of employees leaving is equal to the number of employees moving in. For example if n = 3 and two employees are leaving building 0, one is leaving building 1, and one is leaving building 2, there should be two employees moving to building 0, one employee moving to building 1, and one employee moving to building 2.
Return the maximum number of achievable requests.
Example 1:

Input: n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]] Output: 5 Explantion: Let's see the requests: From building 0 we have employees x and y and both want to move to building 1. From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively. From building 2 we have employee z and they want to move to building 0. From building 3 we have employee c and they want to move to building 4. From building 4 we don't have any requests. We can achieve the requests of users x and b by swapping their places. We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.
Example 2:
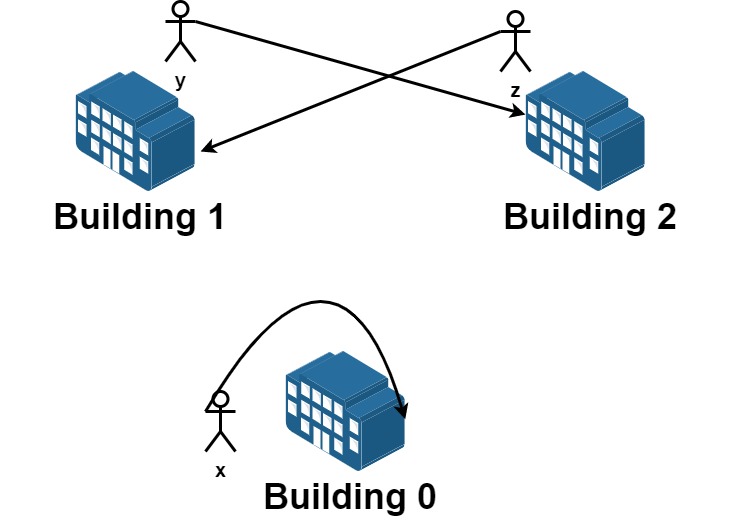
Input: n = 3, requests = [[0,0],[1,2],[2,1]] Output: 3 Explantion: Let's see the requests: From building 0 we have employee x and they want to stay in the same building 0. From building 1 we have employee y and they want to move to building 2. From building 2 we have employee z and they want to move to building 1. We can achieve all the requests.
Example 3:
Input: n = 4, requests = [[0,3],[3,1],[1,2],[2,0]] Output: 4
Constraints:
1 <= n <= 201 <= requests.length <= 16requests[i].length == 20 <= fromi, toi < n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the number of buildings and the number of transfer requests? Are they small enough that a brute-force approach is not viable?
- Are the building numbers guaranteed to be within a specific range, or can they be arbitrarily large?
- If no transfer requests can be fulfilled, should I return 0, or is there another specified return value?
- Are duplicate transfer requests allowed? If so, does fulfilling one transfer request twice count as two achieved transfers?
- Is it possible for a building to request a transfer to itself (i.e., `from` and `to` are the same for a request)? How should I handle such cases?
Brute Force Solution
Approach
The brute force approach involves checking every possible combination of transfer requests. We explore each subset of requests to find the largest set where all transfers can be fulfilled simultaneously.
Here's how the algorithm would work step-by-step:
- Consider all possible groups of transfer requests, starting from a group containing no requests at all.
- For each group of requests, check if it's possible to fulfill all the requests in that group without violating any building's capacity.
- To check if a group is possible, calculate the net change in capacity for each building if those transfers happen.
- If any building ends up with a negative capacity after the transfers, the group is not possible, and we discard it.
- If all buildings have non-negative capacities after the transfers, the group is possible, and we record the number of requests in that group.
- After checking all possible groups, find the group with the largest number of requests that was possible.
- The number of requests in that largest possible group is the maximum number of achievable transfer requests.
Code Implementation
def maximum_achievable_transfer_requests(number_of_buildings, requests):
maximum_achieved_requests = 0
# Iterate through all possible combinations of requests
for i in range(1 << len(requests)):
current_requests = []
for j in range(len(requests)):
if (i >> j) & 1:
current_requests.append(requests[j])
building_changes = [0] * number_of_buildings
# Calculate net change for each building.
for request in current_requests:
building_changes[request[0]] -= 1
building_changes[request[1]] += 1
possible = True
# Verify buildings never have negative capacities.
for change in building_changes:
if change < 0:
possible = False
break
#If the subset is possible, update maximum requests.
if possible:
maximum_achieved_requests = max(maximum_achieved_requests, len(current_requests))
return maximum_achieved_requestsBig(O) Analysis
Optimal Solution
Approach
This problem asks us to find the largest set of transfer requests we can fulfill without creating an imbalance. The key idea is to focus on tracking the net change in the number of employees at each building and accepting only request cycles that don't change that balance.
Here's how the algorithm would work step-by-step:
- First, calculate the net change in employees for each building. For each transfer request, count one employee leaving the 'from' building and one employee arriving at the 'to' building.
- After processing all requests, check if the net change for every building is zero. If it is, all requests can be granted.
- If not all requests can be granted, look for cycles of requests where people are essentially being swapped between buildings. Imagine a closed loop where employees are only moving around *within* the loop.
- To find the maximum number of achievable requests, first assume we grant *none* of the requests. Then, systematically try granting requests (or combinations of requests) that don't affect the overall balance (net change).
- Specifically, try to identify cycles in the requests. For example, if building A sends someone to building B, building B sends someone to building C, and building C sends someone to building A, that's a cycle and can be fulfilled without affecting the balance.
- Keep track of the largest number of requests that form valid cycles that can be granted at the same time. This will be your final answer.
Code Implementation
def maximum_requests(number_of_buildings, requests):
number_of_requests = len(requests)
max_achievable_requests = 0
for i in range(1 << number_of_requests):
# Determine which requests are included in the current subset.
current_requests = []
count = 0
for j in range(number_of_requests):
if (i >> j) & 1:
current_requests.append(requests[j])
count += 1
# Calculate the net change in employees for each building.
net_change = [0] * number_of_buildings
for start_building, end_building in current_requests:
net_change[start_building] -= 1
net_change[end_building] += 1
# Check if the net change for every building is zero.
is_valid = all(change == 0 for change in net_change)
# If all requests can be granted, update max_achievable_requests
if is_valid:
max_achievable_requests = max(max_achievable_requests, count)
return max_achievable_requestsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty buildings array | Return 0 if the buildings array is null or empty, as there are no requests to process. |
| Empty requests array | Return 0 if the requests array is empty, as no transfers are being made. |
| Single building and multiple requests to/from it | The flow tracking mechanism will account for the building's net balance and the maximum achievable is requests that balance each other. |
| Maximum number of buildings and requests (n=20, requests = n*(n-1)) | The algorithm must be efficient enough to handle the maximum input size, considering time and space complexity (e.g., use efficient data structures to prevent time out). |
| All requests are to the same building | Check balance constraints for each node and if there's no building with a negative balance, increment the count otherwise do not. |
| All requests are from the same building | The flow tracking mechanism will account for the building's net balance and the maximum achievable is requests that balance each other. |
| Cyclic dependencies where transfers create cycles of imbalance | The flow tracking will correctly represent a cycle and only valid transfers will be counted. |
| Integer overflow in calculating building balances | Ensure the data type used for calculating balances (e.g., long) can accommodate the maximum possible net flow for a building to prevent integer overflow. |