Maximum Number of Points From Grid Queries

Hard

Asked by:

20 views

Topics:

ArraysGraphsDynamic Programming

You are given an m x n integer matrix grid and an array queries of size k.

Find an array answer of size k such that for each integer queries[i] you start in the top left cell of the matrix and repeat the following process:

If queries[i] is strictly greater than the value of the current cell that you are in, then you get one point if it is your first time visiting this cell, and you can move to any adjacent cell in all 4 directions: up, down, left, and right.
Otherwise, you do not get any points, and you end this process.

After the process, answer[i] is the maximum number of points you can get. Note that for each query you are allowed to visit the same cell multiple times.

Return the resulting array answer.

Example 1:

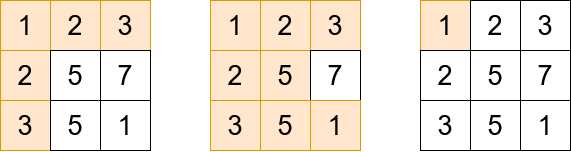
Input: grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
Output: [5,8,1]
Explanation: The diagrams above show which cells we visit to get points for each query.

Example 2:

Input: grid = [[5,2,1],[1,1,2]], queries = [3]
Output: [0]
Explanation: We can not get any points because the value of the top left cell is already greater than or equal to 3.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 10⁵
k == queries.length
1 <= k <= 10⁴
1 <= grid[i][j], queries[i] <= 10⁶

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions (number of rows and columns) of the grid, and what are the possible ranges for the values within the grid?
What are the possible values for the queries, and can the queries array be empty?
Can the grid contain negative values, zero, or only positive integers?
If a query value is smaller than or equal to the starting cell's value (grid[0][0]), what should the corresponding point count be for that query? Should it be 0?
Are there any constraints on the number of queries I should expect?

Brute Force Solution

Approach

The brute force strategy explores every single possible path through the grid for each query. For each query value, we visit cells, accumulating points as we go, and exhaustively try every possible path from the top-left cell.

Here's how the algorithm would work step-by-step:

For each query value, start at the top-left cell of the grid and mark it as visited, and add its value to your points.
From the current cell, try moving to all valid adjacent cells (up, down, left, right).
If moving to a new cell will give you more points (the cell's value is less than the current query), mark it as visited, add its value to your points, and remember that path and the number of points you've accumulated.
If a move doesn't give you more points (cell value is greater than the current query), do not take the path.
Keep going down all the valid paths until you cannot visit any new cells for each starting step.
Remember the path that leads to the largest number of points from those possible paths.
After trying all possible paths from the start, give the result of the optimal one.

Code Implementation

def maximum_points_from_grid_queries_brute_force(grid, queries):
    number_of_rows = len(grid)
    number_of_columns = len(grid[0])
    results = []

    for query in queries:
        maximum_points = 0

        def explore_paths(row_index, column_index, current_points, visited_cells):
            nonlocal maximum_points
            
            #The value of current cell has to be added
            current_points += grid[row_index][column_index]

            maximum_points = max(maximum_points, current_points)

            # Check all possible paths from current cell
            possible_moves = [(0, 1), (0, -1), (1, 0), (-1, 0)]

            for row_move, column_move in possible_moves:
                new_row_index = row_index + row_move
                new_column_index = column_index + column_move

                # Check move validity
                if 0 <= new_row_index < number_of_rows and 0 <= new_column_index < number_of_columns:
                    # Avoid revisiting cells and exceeding query
                    if (new_row_index, new_column_index) not in visited_cells and grid[new_row_index][new_column_index] < query:
                        new_visited_cells = visited_cells.copy()
                        new_visited_cells.add((new_row_index, new_column_index))
                        explore_paths(new_row_index, new_column_index, current_points, new_visited_cells)

        #Start exploring all paths from the top-left cell.
        explore_paths(0, 0, 0, {(0, 0)})
        results.append(maximum_points)

    return results

Big(O) Analysis

Time Complexity

O((m*n)^(m*n)*q) – The brute force approach explores all possible paths in an m x n grid for each query. In the worst case, we might visit each cell multiple times along different paths. The number of possible paths can grow exponentially with the grid size, potentially visiting all m*n cells in each path. Therefore, the number of paths can be approximated by (m*n)^(m*n) since each cell has up to 4 choices, which can be bounded above by m*n. Since this is done for q queries, the total time complexity becomes O((m*n)^(m*n)*q), where q is the number of queries.

Space Complexity

O(2^(R*C)) – The brute force approach explores all possible paths in the grid using recursion. In the worst-case scenario, where R is the number of rows and C is the number of columns, each cell can potentially have multiple unvisited neighbors leading to an exponential number of paths. Each path considered could be stored on the recursion call stack and/or in the 'remembered path', and the number of paths can grow exponentially with the size of the grid R*C. Thus, the space complexity becomes O(2^(R*C)), because the number of possible paths may grow exponentially.

Optimal Solution

Approach

The problem asks us to find the maximum points achievable from a grid, given a set of queries. The optimal strategy involves exploring the grid in a way that prioritizes cells with lower values, allowing us to efficiently determine the number of reachable cells for each query.

Here's how the algorithm would work step-by-step:

First, sort the queries from smallest to largest.
Imagine starting at the top-left corner of the grid.
Explore the grid, always moving to neighboring cells with values less than the current query's value.
Keep track of which cells you've already visited to avoid counting them multiple times.
For each query, count how many cells you could reach based on the value of the query. This is the number of cells with smaller values.
Because the queries were sorted, you can re-use information from previous queries and don't need to re-explore the whole grid for each query. Just explore any new cells that have values smaller than the current query's value, but greater than the previous query.
Store the results so the answer to each query matches its original order.

Code Implementation

def maximum_number_of_points(grid, queries):
    rows = len(grid)
    cols = len(grid[0])
    number_of_queries = len(queries)
    
    # Store the original index with each query for later use
    indexed_queries = sorted([(value, index) for index, value in enumerate(queries)])
    
    answers = [0] * number_of_queries
    visited = set()
    reachable_cells = 0
    
    def explore(row, col, threshold):
        if (row < 0 or row >= rows or col < 0 or col >= cols or
            (row, col) in visited or grid[row][col] >= threshold):
            return
        
        visited.add((row, col))
        nonlocal reachable_cells
        reachable_cells += 1

        explore(row + 1, col, threshold)
        explore(row - 1, col, threshold)
        explore(row, col + 1, threshold)
        explore(row, col - 1, threshold)

    row = 0
    col = 0
    # Sort queries to efficiently explore the grid
    for query_value, original_index in indexed_queries:
        if not visited:
            if grid[0][0] < query_value:
                explore(0, 0, query_value)
        else:
            # Continue exploring from previously visited cells
            new_visited = visited.copy()
            for row_index in range(rows):
                for col_index in range(cols):
                    if (row_index, col_index) not in visited and grid[row_index][col_index] < query_value:
                        explore(row_index, col_index, query_value)

        answers[original_index] = reachable_cells

    return answers

Big(O) Analysis

Time Complexity

O(m * n * log(m * n) + q * log(q)) – Let m and n be the dimensions of the grid, and q be the number of queries. Sorting the queries initially takes O(q * log(q)) time. The core of the algorithm involves exploring the grid, potentially visiting each cell. In the worst case, for each query, we might need to explore all m * n cells, but we avoid re-exploring cells already visited for previous queries. Using a priority queue to efficiently explore the grid cells in increasing order can take O(log(m*n)) per cell, resulting in O(m * n * log(m * n)). Therefore, the overall time complexity is dominated by the grid traversal and the initial sort, approximating to O(m * n * log(m * n) + q * log(q)).

Space Complexity

O(M * N + K) – The algorithm uses auxiliary space for several purposes. Firstly, it needs a visited array of size M * N, where M and N are the dimensions of the grid, to keep track of visited cells during exploration. Secondly, it needs space to store the sorted queries, which takes O(K) space, where K is the number of queries. Finally, space is used to store the answer for each query, which also takes O(K) space. Therefore, the overall space complexity is O(M * N + K + K), which simplifies to O(M * N + K).

Edge Cases

Case	How to Handle
Empty grid or empty queries array	Return an empty result list as there are no points to collect or no queries to process.
Single cell grid (1x1)	Compare the single cell's value to each query and return 1 if the cell's value is less than the query; otherwise, return 0.
Queries with identical values	Ensure the algorithm correctly processes queries with the same value, potentially re-traversing the grid for each identical query if necessary.
Grid with all identical values	The algorithm should efficiently count the number of cells visited before encountering a value greater than a query, or visit all cells if none are greater.
Queries are monotonically increasing	Optimize the solution to potentially avoid re-exploring already visited cells for subsequent larger queries.
Integer overflow when calculating points or managing priority queue size	Use appropriate data types (e.g., long) to handle potentially large point values or sizes.
Maximum sized grid and queries array (scaling)	The chosen algorithm (e.g., Dijkstra with priority queue) must be efficient enough to handle the maximum input size within the time limit (consider space complexity as well).
Grid containing zero or negative values	The algorithm should handle zero and negative values in the grid without errors, correctly comparing them to query values.

Empty grid or empty queries array

How to Handle:

Return an empty result list as there are no points to collect or no queries to process.

Single cell grid (1x1)

How to Handle:

Compare the single cell's value to each query and return 1 if the cell's value is less than the query; otherwise, return 0.

Queries with identical values

How to Handle:

Ensure the algorithm correctly processes queries with the same value, potentially re-traversing the grid for each identical query if necessary.

Grid with all identical values

How to Handle:

The algorithm should efficiently count the number of cells visited before encountering a value greater than a query, or visit all cells if none are greater.

Queries are monotonically increasing

How to Handle:

Optimize the solution to potentially avoid re-exploring already visited cells for subsequent larger queries.

Integer overflow when calculating points or managing priority queue size

How to Handle:

Use appropriate data types (e.g., long) to handle potentially large point values or sizes.

Maximum sized grid and queries array (scaling)

How to Handle:

The chosen algorithm (e.g., Dijkstra with priority queue) must be efficient enough to handle the maximum input size within the time limit (consider space complexity as well).

Grid containing zero or negative values

How to Handle:

The algorithm should handle zero and negative values in the grid without errors, correctly comparing them to query values.