Maximum Path Quality of a Graph

Hard

SAP

1 view

Topics:

GraphsRecursion

There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the i^th node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [u_j, v_j, time_j] indicates that there is an undirected edge between the nodes u_j and v_j,and it takes time_j seconds to travel between the two nodes. Finally, you are given an integer maxTime.

A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node's value is added at most once to the sum).

Return the maximum quality of a valid path.

Note: There are at most four edges connected to each node.

Example 1:

Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
Output: 75
Explanation:
One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.

Example 2:

Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
Output: 25
Explanation:
One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30.
The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.

Example 3:

Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
Output: 7
Explanation:
One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.

Constraints:

n == values.length
1 <= n <= 1000
0 <= values[i] <= 10⁸
0 <= edges.length <= 2000
edges[j].length == 3
0 <= u_j< v_j <= n - 1
10 <= time_j, maxTime <= 100
All the pairs [u_j, v_j] are unique.
There are at most four edges connected to each node.
The graph may not be connected.

Try coding it in LeetCode

Maximum Path Quality of a Graph

Hard

SAP

1 view

Topics:

GraphsRecursion

There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the i^th node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [u_j, v_j, time_j] indicates that there is an undirected edge between the nodes u_j and v_j,and it takes time_j seconds to travel between the two nodes. Finally, you are given an integer maxTime.

A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node's value is added at most once to the sum).

Return the maximum quality of a valid path.

Note: There are at most four edges connected to each node.

Example 1:

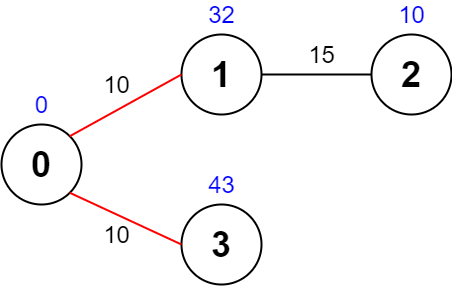
Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
Output: 75
Explanation:
One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.

Example 2:

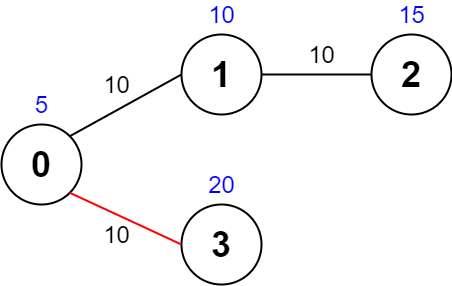
Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
Output: 25
Explanation:
One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30.
The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.

Example 3:

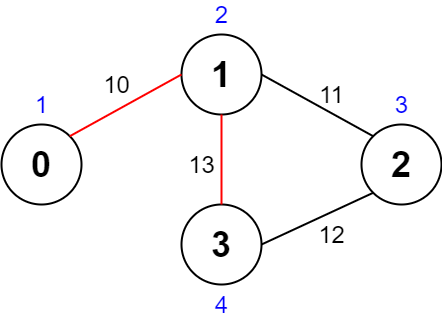
Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
Output: 7
Explanation:
One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.

Constraints:

n == values.length
1 <= n <= 1000
0 <= values[i] <= 10⁸
0 <= edges.length <= 2000
edges[j].length == 3
0 <= u_j< v_j <= n - 1
10 <= time_j, maxTime <= 100
All the pairs [u_j, v_j] are unique.
There are at most four edges connected to each node.
The graph may not be connected.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the number of nodes and edges in the graph? What is the maximum value of `maxTime`?
Can the `values` array contain negative values or zero? Are the time costs associated with the edges always positive?
Is it guaranteed that there is always a path from node 0 back to node 0 within the given `edges` and `maxTime`?
If no valid path exists (starting and ending at node 0 within `maxTime`), what value should I return?
Are multiple edges allowed between the same two nodes? If so, should I consider the edge with the smallest time cost?

Brute Force Solution

Approach

The brute force method for finding the maximum path quality in a graph involves exploring every possible route within the allowed time. We visit nodes one by one, trying every possible path, and calculating the quality for each path.

Here's how the algorithm would work step-by-step:

Start at the starting node.
From the current node, explore every possible next node you can reach within the time limit.
Keep track of the nodes you've visited to avoid going in circles and wasting time.
For each path, calculate the total quality by adding up the values of the nodes visited, but only count a node's value the first time you visit it.
If a path reaches the starting node again, record its quality and the time taken.
Continue exploring all possible paths until you've exhausted all options within the time limit.
Compare the quality of all the paths that returned to the start and pick the one with the highest quality.

Code Implementation

def maximum_path_quality_brute_force(values, edges, max_time):
    number_of_nodes = len(values)
    maximum_quality = 0

    def depth_first_search(current_node, current_time, current_quality, visited_nodes):
        nonlocal maximum_quality

        # If we return to the starting node, update the maximum quality
        if current_node == 0:
            maximum_quality = max(maximum_quality, current_quality)

        # Explore neighbors
        for neighbor, time_to_neighbor in edges[current_node]:
            if current_time + time_to_neighbor <= max_time:
                new_quality = current_quality
                if neighbor not in visited_nodes:
                    new_quality += values[neighbor]

                # Add neighbor to visited nodes to track value adding
                new_visited_nodes = visited_nodes.copy()
                new_visited_nodes.add(neighbor)

                depth_first_search(neighbor, current_time + time_to_neighbor, new_quality, new_visited_nodes)

    # Represent graph as adjacency list.
    adjacency_list = [[] for _ in range(number_of_nodes)]
    for node1, node2, time in edges:
        adjacency_list[node1].append((node2, time))
        adjacency_list[node2].append((node1, time))

    # Initialize visited nodes
    initial_visited_nodes = {0}
    
    # Initiate DFS from the starting node.
    depth_first_search(0, 0, values[0], initial_visited_nodes)

    return maximum_quality

Big(O) Analysis

Time Complexity

O(V^D) – The brute force approach explores all possible paths in the graph starting from node 0. In the worst case, we might visit every node multiple times. Let V be the number of vertices and D be the maximum allowed time (which limits the depth/length of the paths). For each node, we might have multiple choices to explore, leading to an exponential branching factor. Therefore, the total number of paths explored can grow exponentially with the depth of the search, making the time complexity O(V^D), where we are potentially visiting nodes multiple times to fully explore every single path back to the starting node within the time limit. This is a gross overestimation but captures the nature of brute-force searching all paths.

Space Complexity

O(N) – The described brute force algorithm utilizes a visited array to keep track of visited nodes to avoid cycles, where N is the number of nodes in the graph. Additionally, the recursion stack's depth can grow up to N in the worst-case scenario, corresponding to the length of the longest possible path without cycles. Therefore, the auxiliary space is dominated by the visited array and the recursion stack, both of which can grow linearly with the number of nodes.

Optimal Solution

Approach

The problem asks us to find the best path through a network, maximizing a 'quality' score while limited by a travel budget. We explore possible paths step-by-step, remembering visited locations to avoid unnecessary revisits within our budget, and keep track of the best quality found so far.

Here's how the algorithm would work step-by-step:

Start at the designated starting location and use up the value of that location from our quality score.
Consider every possible path we can take from our current location.
Before taking a path, make sure we have enough budget left to travel that path and visit the next location.
If we do have enough budget, 'travel' down the path to the next location.
When we arrive at a new location, add its location value to our quality score if it's the first time we've been there. Remember that we have visited this location.
Repeat steps 2-5 from this new location, trying all available paths, until we either run out of budget or arrive back at the starting location.
If we've arrived back at the starting location, compare the quality score of this path to the best quality score we've seen so far, and update our best score if this path is better.
When exploring the path from each location, make sure to explore all paths. Also, take note of the locations we've visited for future explorations.
To avoid getting stuck in endless loops, do not revisit a location more times than necessary or if we have already obtained its value.
After we have checked all available paths, the best quality score that we saved is our final result.

Code Implementation

def maximum_path_quality(values, edges, max_time):
    number_of_nodes = len(values)
    adjacency_list = [[] for _ in range(number_of_nodes)]

    for source, destination, time_taken in edges:
        adjacency_list[source].append((destination, time_taken))
        adjacency_list[destination].append((source, time_taken))

    max_quality = 0
    visited_counts = [0] * number_of_nodes

    def depth_first_search(current_node, current_time, current_quality):
        nonlocal max_quality

        if current_node == 0:
            max_quality = max(max_quality, current_quality)

        # Explore neighbors.
        for neighbor, time_to_neighbor in adjacency_list[current_node]:
            if current_time + time_to_neighbor <= max_time:

                # Add the neighbor's value if it hasn't been visited yet.
                if visited_counts[neighbor] == 0:
                    visited_counts[neighbor] += 1
                    depth_first_search(neighbor, current_time + time_to_neighbor, current_quality + values[neighbor])
                    visited_counts[neighbor] -= 1

                # If already visited, do not add the value again.
                else:
                    visited_counts[neighbor] += 1
                    depth_first_search(neighbor, current_time + time_to_neighbor, current_quality)
                    visited_counts[neighbor] -= 1

    # Start DFS from node 0, marking it as visited.
    visited_counts[0] = 1
    depth_first_search(0, 0, values[0])

    return max_quality

Big(O) Analysis

Time Complexity

O(V + E * (2^V)) – The algorithm explores all possible paths in the graph using a depth-first search (DFS). The worst-case scenario involves visiting each vertex V and edge E multiple times. Because the problem allows revisiting nodes, in the worst case, we might consider all subsets of nodes. For each edge, we explore the different paths which are influenced by the nodes we have and haven't visited already, which would be a maximum of 2^V. Therefore, the complexity is O(V + E * (2^V)), where V is the number of vertices and E is the number of edges.

Space Complexity

O(N) – The auxiliary space is dominated by the 'visited' array used to track which nodes have been visited and how many times. In the worst-case scenario, the algorithm might visit all N nodes (where N is the number of nodes in the graph). The recursion depth also contributes to the space complexity, potentially reaching N in the worst case if the graph is a long chain. Therefore, the overall auxiliary space complexity is O(N) due to the visited array and potentially the call stack.

Edge Cases

Case	How to Handle
Null or empty values array	Return 0 as no path exists.
Null or empty edges array	If maxTime allows a round trip to node 0, return values[0], otherwise return 0.
Single node graph (values array length is 1) and no edges	If maxTime is greater or equal to 0, return values[0], otherwise 0.
Graph with no path back to node 0 within maxTime	Return 0 as no valid path meets the criteria.
Large graph with deep recursion exceeding stack limits	Consider iterative DFS or BFS to avoid stack overflow.
Edges with very large time costs leading to potential integer overflow	Use long data type for time costs and accumulated path time.
Cycle in the graph that exceeds maxTime if followed repeatedly	Implement a mechanism to prevent infinite loops by tracking visited nodes and time elapsed or limiting visit count of each node.
maxTime is 0 and values[0] is non-zero	If a path from node 0 back to node 0 is possible within time 0, the quality should be values[0]; otherwise, it should be 0.