Maximum Profit in Job Scheduling
Maximum Profit in Job Scheduling #3 Most Asked
HardWe have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].
You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.
If you choose a job that ends at time X you will be able to start another job that starts at time X.
Example 1:

Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70] Output: 120 Explanation: The subset chosen is the first and fourth job. Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.
Example 2:
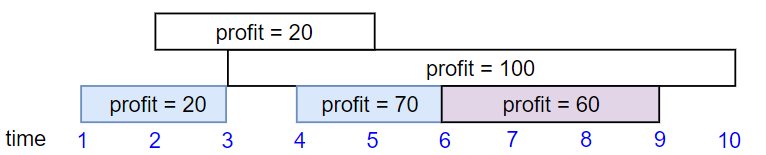
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60] Output: 150 Explanation: The subset chosen is the first, fourth and fifth job. Profit obtained 150 = 20 + 70 + 60.
Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4] Output: 6
Constraints:
1 <= startTime.length == endTime.length == profit.length <= 5 * 1041 <= startTime[i] < endTime[i] <= 1091 <= profit[i] <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the possible ranges for start times, end times, and profits? Can they be negative or zero?
- Is it guaranteed that for any job, the end time will always be strictly greater than its start time?
- If multiple jobs have the exact same start and end times, are they considered distinct jobs that can be chosen independently?
- If no jobs can be selected without overlap, what should be returned as the maximum profit?
- Can the input list of jobs be empty? If so, what is the expected output?
Brute Force Solution
Approach
The problem asks us to find the maximum profit we can make by scheduling a set of jobs, where each job has a start time, end time, and a profit. The brute force approach involves considering every possible combination of jobs that can be performed without any overlap.
Here's how the algorithm would work step-by-step:
- Consider each job one by one.
- For each job, decide whether to include it in our schedule or not.
- If we decide to include a job, we must ensure that it does not overlap with any other job already chosen for the schedule.
- If it overlaps, we cannot include this job with the current selection.
- If it does not overlap, we add its profit to the total profit for this specific combination of jobs.
- We repeat this decision-making process for all jobs, exploring all possible subsets of jobs.
- For every valid schedule (where no jobs overlap), we calculate the total profit.
- Finally, we compare the total profits from all valid schedules and select the largest one as our maximum profit.
Code Implementation
def maximum_profit_job_scheduling_brute_force(jobs):
number_of_jobs = len(jobs)
maximum_profit_found = 0
# Iterate through all possible subsets of jobs (2^n combinations)
for i in range(1 << number_of_jobs):
current_schedule_profit = 0
current_schedule_jobs = []
# Build a potential schedule for the current subset
for j in range(number_of_jobs):
# Check if the j-th job is included in the current subset
if (i >> j) & 1:
job_start_time = jobs[j][0]
job_end_time = jobs[j][1]
job_profit = jobs[j][2]
is_overlap = False
# Ensure the new job doesn't overlap with already selected jobs
for scheduled_job_start, scheduled_job_end, _ in current_schedule_jobs:
if max(job_start_time, scheduled_job_start) < min(job_end_time, scheduled_job_end):
is_overlap = True
break
# If no overlap, add the job to the current schedule
if not is_overlap:
current_schedule_jobs.append((job_start_time, job_end_time, job_profit))
current_schedule_profit += job_profit
# Update the overall maximum profit if the current schedule is better
maximum_profit_found = max(maximum_profit_found, current_schedule_profit)
return maximum_profit_foundBig(O) Analysis
Optimal Solution
Approach
The most efficient way to solve this involves sorting the jobs by their end times and then carefully deciding whether to take a job or skip it. We aim to maximize profit by making a series of choices that consider both the potential gain of a job and its impact on future opportunities.
Here's how the algorithm would work step-by-step:
- First, organize all the jobs based on when they finish. Jobs that end sooner should come before those that end later.
- Imagine you are building up the maximum profit you can achieve. For each job, consider two main possibilities: either you include this job in your schedule, or you don't.
- If you decide to take a particular job, you get its profit. However, you can only take this job if it doesn't overlap with any previous jobs you've already decided to schedule. Specifically, you need to find the latest finishing job among those you've already committed to that ends before this new job begins.
- The profit you get from taking the current job is its own profit plus the maximum profit you could have made from all the jobs that finished before this one started.
- If you decide not to take the current job, the maximum profit you can achieve up to this point is simply the maximum profit you could have made from the jobs before it.
- For each job, you compare the profit you get by taking it (plus earlier compatible profits) with the profit you get by skipping it. You always choose the option that gives you more profit.
- By systematically going through each job in order of their finish times and making this best choice at each step, you build up the overall maximum profit you can achieve for the entire set of jobs.
Code Implementation
def find_maximum_profit_in_job_scheduling(job_start_times, job_end_times, job_profits):
number_of_jobs = len(job_start_times)
jobs = []
for index in range(number_of_jobs):
jobs.append((job_start_times[index], job_end_times[index], job_profits[index]))
# Sort jobs by their end times to process them in chronological order.
jobs.sort(key=lambda x: x[1])
# Initialize a list to store the maximum profit achievable up to each job's end time.
# The length is number_of_jobs + 1 to handle the base case of no jobs.
maximum_profits = [0] * (number_of_jobs + 1)
for index in range(1, number_of_jobs + 1):
current_start_time, current_end_time, current_profit = jobs[index - 1]
# Find the latest job that finishes before the current job starts.
# This is crucial for ensuring non-overlapping job selections.
previous_compatible_job_index = 0
for prev_index in range(index - 1, 0, -1):
if jobs[prev_index - 1][1] <= current_start_time:
previous_compatible_job_index = prev_index
break
# Decide whether to include the current job or skip it to maximize profit.
# Profit if including: current job's profit + max profit from compatible previous jobs.
profit_if_included = current_profit + maximum_profits[previous_compatible_job_index]
# Profit if skipping: the max profit achieved considering jobs before this one.
profit_if_skipped = maximum_profits[index - 1]
# Store the maximum profit achievable considering jobs up to the current one.
maximum_profits[index] = max(profit_if_included, profit_if_skipped)
return maximum_profits[number_of_jobs]Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty list of jobs | An empty job list should result in a maximum profit of 0. |
| Single job in the list | If there's only one job, the maximum profit is simply the profit of that single job. |
| All jobs have zero profit | The algorithm should correctly return 0 if all jobs offer no profit. |
| Jobs with identical start and end times | Jobs with zero duration should be handled correctly, typically by considering their profit if they don't overlap with other non-zero duration jobs. |
| Jobs with overlapping times but no possible valid schedule | The solution should return 0 if no jobs can be selected without overlap. |
| A very large number of jobs | The chosen algorithm (likely dynamic programming with binary search for finding the previous non-overlapping job) should be efficient enough (n log n) to handle large inputs within typical time limits. |
| Extremely large profit values that might cause integer overflow | Use 64-bit integers (long long in C++ or standard integers in Python which handle arbitrary precision) for profit calculations to prevent overflow. |
| Jobs are not initially sorted | The solution relies on sorting jobs by their end times, so the first step must be to sort the input job list. |