Maximum Score From Grid Operations

Hard

Hudson River Trading

1 view

Topics:

ArraysDynamic Programming

You are given a 2D matrix grid of size n x n. Initially, all cells of the grid are colored white. In one operation, you can select any cell of indices (i, j), and color black all the cells of the j^th column starting from the top row down to the i^th row.

The grid score is the sum of all grid[i][j] such that cell (i, j) is white and it has a horizontally adjacent black cell.

Return the maximum score that can be achieved after some number of operations.

Example 1:

Input: grid = [[0,0,0,0,0],[0,0,3,0,0],[0,1,0,0,0],[5,0,0,3,0],[0,0,0,0,2]]

Output: 11

Explanation:

In the first operation, we color all cells in column 1 down to row 3, and in the second operation, we color all cells in column 4 down to the last row. The score of the resulting grid is grid[3][0] + grid[1][2] + grid[3][3] which is equal to 11.

Example 2:

Input: grid = [[10,9,0,0,15],[7,1,0,8,0],[5,20,0,11,0],[0,0,0,1,2],[8,12,1,10,3]]

Output: 94

Explanation:

We perform operations on 1, 2, and 3 down to rows 1, 4, and 0, respectively. The score of the resulting grid is grid[0][0] + grid[1][0] + grid[2][1] + grid[4][1] + grid[1][3] + grid[2][3] + grid[3][3] + grid[4][3] + grid[0][4] which is equal to 94.

Constraints:

1 <= n == grid.length <= 100
n == grid[i].length
0 <= grid[i][j] <= 10⁹

Maximum Score From Grid Operations

Hard

Hudson River Trading

1 view

Topics:

ArraysDynamic Programming

You are given a 2D matrix grid of size n x n. Initially, all cells of the grid are colored white. In one operation, you can select any cell of indices (i, j), and color black all the cells of the j^th column starting from the top row down to the i^th row.

The grid score is the sum of all grid[i][j] such that cell (i, j) is white and it has a horizontally adjacent black cell.

Return the maximum score that can be achieved after some number of operations.

Example 1:

Input: grid = [[0,0,0,0,0],[0,0,3,0,0],[0,1,0,0,0],[5,0,0,3,0],[0,0,0,0,2]]

Output: 11

Explanation:

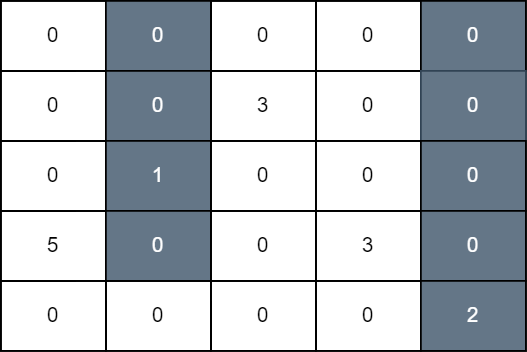
In the first operation, we color all cells in column 1 down to row 3, and in the second operation, we color all cells in column 4 down to the last row. The score of the resulting grid is grid[3][0] + grid[1][2] + grid[3][3] which is equal to 11.

Example 2:

Input: grid = [[10,9,0,0,15],[7,1,0,8,0],[5,20,0,11,0],[0,0,0,1,2],[8,12,1,10,3]]

Output: 94

Explanation:

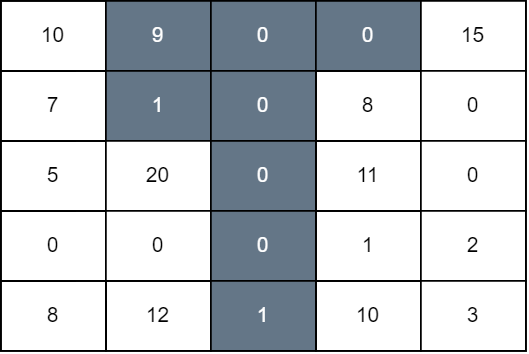
We perform operations on 1, 2, and 3 down to rows 1, 4, and 0, respectively. The score of the resulting grid is grid[0][0] + grid[1][0] + grid[2][1] + grid[4][1] + grid[1][3] + grid[2][3] + grid[3][3] + grid[4][3] + grid[0][4] which is equal to 94.

Constraints:

1 <= n == grid.length <= 100
n == grid[i].length
0 <= grid[i][j] <= 10⁹

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the grid (rows and columns)? What are the maximum possible values for each dimension?
Can the grid values be negative, zero, or only positive integers?
Is the grid guaranteed to be non-empty (at least one row and one column)? What should I return if the grid is empty or null?
Are there any constraints on the data types used to represent the grid values? (e.g., 32-bit integer, 64-bit integer)
If there are multiple paths that result in the maximum score, do I need to return a specific one, or can I return any one of them?

Brute Force Solution

Approach

The brute force strategy for maximizing the score from grid operations involves exploring every possible path from the starting point to the end. It's like trying out all the routes you could take through a maze to find the one that gives you the highest score.

Here's how the algorithm would work step-by-step:

Start at the beginning of the grid.
Consider every possible direction you can move from your current spot. Let's say you can move up, down, left, or right.
For each possible move, calculate the score you would get by making that move.
Record the path you took and the total score you have at that point.
From each of your new spots, again consider all possible moves and calculate the score for each of those moves.
Keep repeating this process, creating every possible path through the grid until you reach the end point or cannot move anymore.
Once you've explored all possible paths, compare the total scores from each path.
Select the path that gave you the highest overall score. This is the maximum score you can get.

Code Implementation

def maximum_score_from_grid_operations_brute_force(grid):    number_of_rows = len(grid)
    number_of_columns = len(grid[0])

    def get_all_possible_paths(row_index, column_index, current_score):
        # If we reach the end of the grid, return the score.
        if row_index == number_of_rows - 1 and column_index == number_of_columns - 1:
            return current_score + grid[row_index][column_index]

        #If the current cell is out of bounds, return negative infinity.
        if row_index < 0 or row_index >= number_of_rows or column_index < 0 or column_index >= number_of_columns:
            return float('-inf')

        current_score += grid[row_index][column_index]
        grid_value = grid[row_index][column_index]
        grid[row_index][column_index] = 0 # Mark as visited

        # Explore all possible paths from the current cell.
        up = get_all_possible_paths(row_index - 1, column_index, current_score)

        down = get_all_possible_paths(row_index + 1, column_index, current_score)

        left = get_all_possible_paths(row_index, column_index - 1, current_score)

        right = get_all_possible_paths(row_index, column_index + 1, current_score)

        grid[row_index][column_index] = grid_value # Backtrack

        # Find the maximum score among all paths.
        return max(up, down, left, right)

    # Initiate brute force search for all possible paths from start point
    maximum_score = get_all_possible_paths(0, 0, 0)

    return maximum_score

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(4^(m*n)) – The brute force approach explores all possible paths in the grid. From each cell, we can potentially move in four directions (up, down, left, right). In an m x n grid, the maximum path length is proportional to m*n. Therefore, in the worst case, we explore all possible paths of length up to m*n, leading to a branching factor of 4 for each cell visited. This results in a time complexity of O(4^(m*n)), where m is the number of rows and n is the number of columns.

Space Complexity

O(4^N) – The brute force approach explores all possible paths in the grid. In the worst case, from each cell, there can be up to four possible moves (up, down, left, right). The recursion will branch out in all possible directions until it hits a dead end or reaches the target, effectively exploring a tree of possible paths. If N is the number of cells in the grid (rows * cols), the height of this tree can be at most N. Since each node has up to four children, the number of possible paths grows exponentially and the call stack can reach a depth proportional to the number of cells. Therefore, the space complexity is O(4^N) due to the maximum possible size of the recursion call stack.

Optimal Solution

Approach

The goal is to find the highest possible score you can get by moving through a grid, adding and subtracting values. The best way to solve this is to realize it's a classic pathfinding problem where we can avoid recomputing scores using dynamic programming, saving a lot of time.

Here's how the algorithm would work step-by-step:

Think of the grid as a map and each cell as a location. You start at the top left and want to reach the bottom right.
Instead of trying every possible path, which would take forever, imagine building a table. This table will store the best score you can get to reach any particular cell.
Start filling out the table. The top-left cell is easy; it's just the value in that cell.
For each cell, look at the cells directly above it and to the left. Since you can only move right or down, those are the only places you could have come from.
Choose the path that gives you the best score to reach the current cell. That means adding the current cell's value to the better of the two scores from above or left.
Store this best score in the table for the current cell.
Continue this process row by row and column by column until you reach the bottom right. The value in the bottom-right cell of the table will be the maximum possible score you can get.
By storing the best scores to reach each cell, you avoid recalculating the same paths over and over, making the solution much faster.

Code Implementation

def max_score_from_grid_operations(grid):
    number_of_rows = len(grid)
    number_of_columns = len(grid[0])

    # This table stores the maximum score to reach each cell.
    maximum_score_table = [([0] * number_of_columns) for _ in range(number_of_rows)]
    maximum_score_table[0][0] = grid[0][0]

    # Initialize first row.
    for column_index in range(1, number_of_columns):
        maximum_score_table[0][column_index] = maximum_score_table[0][column_index - 1] + grid[0][column_index]

    # Initialize first column.
    for row_index in range(1, number_of_rows):
        maximum_score_table[row_index][0] = maximum_score_table[row_index - 1][0] + grid[row_index][0]

    # Fill the table using dynamic programming.
    for row_index in range(1, number_of_rows):
        for column_index in range(1, number_of_columns):

            # Choose the path with the max score from top/left.
            maximum_score_table[row_index][column_index] = max(
                maximum_score_table[row_index - 1][column_index],
                maximum_score_table[row_index][column_index - 1],
            ) + grid[row_index][column_index]

    # Result holds maximum score to reach bottom right.
    return maximum_score_table[number_of_rows - 1][number_of_columns - 1]

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each cell of the grid once to calculate the maximum score to reach that cell. The grid has 'm' rows and 'n' columns. For each cell, a constant amount of work is performed to look up the best scores from the cells above and to the left. Therefore, the time complexity is proportional to the number of cells in the grid, resulting in O(m*n).

Space Complexity

O(N*M) – The dynamic programming solution described uses a table to store the maximum score to reach each cell. If the grid has N rows and M columns, this table will have dimensions N x M. Therefore, the auxiliary space required is proportional to the number of cells in the grid, which is N*M. This table is the dominant factor in space complexity.

Edge Cases

Case	How to Handle
Null or empty grid	Return 0 if the grid is null or empty, as there are no cells to visit.
Grid with only one row or one column	Iterate through the single row or column and sum the values.
1x1 grid	Return the single cell's value directly.
Grid with negative numbers	The dynamic programming approach should correctly handle negative numbers, potentially leading to negative maximum scores.
Grid with all zeros	The DP solution will correctly compute a maximum score of 0.
Integer overflow in score calculation	Use a larger data type (e.g., long) for the score to avoid integer overflow.
Large grid dimensions that cause memory issues with DP	The DP table should be allocated within available memory limits, and the complexity should be analyzed beforehand.
Grid with extremely large positive and negative values	Ensure that the chosen data type for storing cell values and the accumulated score can accommodate these extreme values without overflow or loss of precision.