Maximum Square Area by Removing Fences From a Field

Medium

Atlassian

2 views

Topics:

Arrays

There is a large (m - 1) x (n - 1) rectangular field with corners at (1, 1) and (m, n) containing some horizontal and vertical fences given in arrays hFences and vFences respectively.

Horizontal fences are from the coordinates (hFences[i], 1) to (hFences[i], n) and vertical fences are from the coordinates (1, vFences[i]) to (m, vFences[i]).

Return the maximum area of a square field that can be formed by removing some fences (possibly none) or -1 if it is impossible to make a square field.

Since the answer may be large, return it modulo 10⁹+ 7.

Note: The field is surrounded by two horizontal fences from the coordinates (1, 1) to (1, n) and (m, 1) to (m, n) and two vertical fences from the coordinates (1, 1) to (m, 1) and (1, n) to (m, n). These fences cannot be removed.

Example 1:

Input: m = 4, n = 3, hFences = [2,3], vFences = [2]
Output: 4
Explanation: Removing the horizontal fence at 2 and the vertical fence at 2 will give a square field of area 4.

Example 2:

Input: m = 6, n = 7, hFences = [2], vFences = [4]
Output: -1
Explanation: It can be proved that there is no way to create a square field by removing fences.

Constraints:

3 <= m, n <= 10⁹
1 <= hFences.length, vFences.length <= 600
1 < hFences[i] < m
1 < vFences[i] < n
hFences and vFences are unique.

Maximum Square Area by Removing Fences From a Field

Medium

Atlassian

2 views

Topics:

Arrays

There is a large (m - 1) x (n - 1) rectangular field with corners at (1, 1) and (m, n) containing some horizontal and vertical fences given in arrays hFences and vFences respectively.

Horizontal fences are from the coordinates (hFences[i], 1) to (hFences[i], n) and vertical fences are from the coordinates (1, vFences[i]) to (m, vFences[i]).

Return the maximum area of a square field that can be formed by removing some fences (possibly none) or -1 if it is impossible to make a square field.

Since the answer may be large, return it modulo 10⁹+ 7.

Note: The field is surrounded by two horizontal fences from the coordinates (1, 1) to (1, n) and (m, 1) to (m, n) and two vertical fences from the coordinates (1, 1) to (m, 1) and (1, n) to (m, n). These fences cannot be removed.

Example 1:

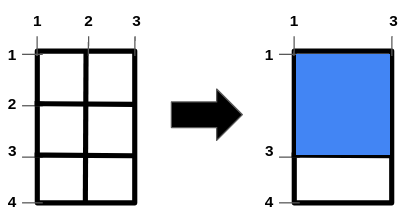
Input: m = 4, n = 3, hFences = [2,3], vFences = [2]
Output: 4
Explanation: Removing the horizontal fence at 2 and the vertical fence at 2 will give a square field of area 4.

Example 2:

Input: m = 6, n = 7, hFences = [2], vFences = [4]
Output: -1
Explanation: It can be proved that there is no way to create a square field by removing fences.

Constraints:

3 <= m, n <= 10⁹
1 <= hFences.length, vFences.length <= 600
1 < hFences[i] < m
1 < vFences[i] < n
hFences and vFences are unique.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on n, the size of the field, and the lengths of `horizontalFences` and `verticalFences`?
Can the fence positions in `horizontalFences` and `verticalFences` be unsorted, and do they include the boundaries of the field (0 and n)?
If no square can be formed after removing fences, what should the function return? Specifically, should I return 0, -1, or throw an exception?
Are the fence positions guaranteed to be integers, or can they be floating-point numbers?
Are duplicate fence positions allowed in either `horizontalFences` or `verticalFences`?

Brute Force Solution

Approach

The brute force approach in this case means trying every possible combination of fence removals to see which one creates the largest square. We essentially look at every single sub-field that can be formed after potentially removing some fences. It's like testing every possible arrangement until we find the biggest square.

Here's how the algorithm would work step-by-step:

Consider all possible pairs of horizontal fences. Each pair defines the top and bottom edges of a potential sub-field.
For each of these sub-fields, consider all possible pairs of vertical fences. Each pair defines the left and right edges.
This creates a potential rectangular sub-field defined by the four chosen fences.
Calculate the area of this rectangular sub-field.
Check if the sub-field is a square (i.e., its width and height are equal).
If it is a square, compare its area to the largest square area found so far.
If the current square's area is larger than the largest seen so far, update the largest square area.
Repeat these steps for every possible combination of horizontal and vertical fences.
After checking all combinations, the largest square area found is the answer.

Code Implementation

def max_square_area_brute_force(horizontal_fences, vertical_fences, field_width, field_height):
    max_area = 0

    # Iterate through all possible combinations of horizontal fence removals
    for i in range(1 << len(horizontal_fences)): 
        removed_horizontal_fences = []
        for j in range(len(horizontal_fences)): 
            if (i >> j) & 1:
                removed_horizontal_fences.append(horizontal_fences[j])
        
        # Iterate through all possible combinations of vertical fence removals
        for k in range(1 << len(vertical_fences)): 
            removed_vertical_fences = []
            for l in range(len(vertical_fences)): 
                if (k >> l) & 1:
                    removed_vertical_fences.append(vertical_fences[l])

            # Add the field boundaries to the fence lists
            all_horizontal_fences = sorted([0, field_height] + [fence for fence in horizontal_fences if fence not in removed_horizontal_fences])
            all_vertical_fences = sorted([0, field_width] + [fence for fence in vertical_fences if fence not in removed_vertical_fences])
            
            # Iterate through all rectangles formed by the remaining fences
            for row_index in range(len(all_horizontal_fences) - 1):
                for col_index in range(len(all_vertical_fences) - 1):
                    height = all_horizontal_fences[row_index + 1] - all_horizontal_fences[row_index]
                    width = all_vertical_fences[col_index + 1] - all_vertical_fences[col_index]

                    # Only process this area if it is a square
                    if height == width:
                        area = height * width

                        # Keep track of maximum square area seen so far
                        max_area = max(max_area, area)

    return max_area

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n^4) – The algorithm iterates through all possible pairs of horizontal fences, resulting in O(n^2) combinations. For each pair of horizontal fences, it iterates through all possible pairs of vertical fences, again resulting in O(n^2) combinations. Inside these nested loops, a constant amount of work is done to calculate the area and check if it's a square. Therefore, the total time complexity is O(n^2 * n^2), which simplifies to O(n^4).

Space Complexity

O(1) – The brute force approach, as described, primarily involves iterating through different combinations of horizontal and vertical fences. It calculates areas and compares them to a running maximum. The space complexity is dominated by the need to store a few variables: the largest square area found so far, temporary variables to calculate the dimensions of sub-fields, and loop counters for iterating through fence combinations. These variables consume a constant amount of extra space, irrespective of the number of fences, denoted as N. Therefore, the space complexity is O(1).

Optimal Solution

Approach

The core idea is to find the largest square that can be formed by using subsets of the given horizontal and vertical fence positions. To avoid checking every possible subset, we'll identify all possible distances between fences and find the largest distance that appears in both the horizontal and vertical sets. This will be the side length of the largest possible square.

Here's how the algorithm would work step-by-step:

First, imagine all the distances you can make using only the horizontal fences and the field's edges. Calculate and store these distances.
Do the same thing for all possible distances using only the vertical fences and field's edges. Store these distances separately.
Now, go through the horizontal distances you calculated. For each horizontal distance, check if the exact same distance is also present in the set of vertical distances.
Keep track of the largest distance you find that exists in both the horizontal and vertical sets. This distance is the side length of the biggest possible square.
Finally, square the side length you found to determine the maximum area of the square you can create.

Code Implementation

def maximum_square_area(field_length, field_width, horizontal_fences, vertical_fences):
    horizontal_fences.extend([0, field_length])
    vertical_fences.extend([0, field_width])

    horizontal_fences.sort()
    vertical_fences.sort()

    horizontal_distances = set()
    for i in range(len(horizontal_fences)): 
        for j in range(i + 1, len(horizontal_fences)): 
            horizontal_distance = horizontal_fences[j] - horizontal_fences[i]
            horizontal_distances.add(horizontal_distance)

    vertical_distances = set()
    #Find all possible distances between vertical fences
    for i in range(len(vertical_fences)): 
        for j in range(i + 1, len(vertical_fences)): 
            vertical_distance = vertical_fences[j] - vertical_fences[i]
            vertical_distances.add(vertical_distance)

    max_square_side = 0
    #Only consider square sizes found in both dimensions
    for distance in horizontal_distances:
        if distance in vertical_distances:
            max_square_side = max(max_square_side, distance)

    if max_square_side == 0:
        return 0

    return max_square_side * max_square_side

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n^2) – Let n be the total number of fences (horizontal plus vertical). Calculating all possible distances between horizontal fences takes O(h^2) time, where h is the number of horizontal fences. Similarly, calculating distances between vertical fences takes O(v^2) time, where v is the number of vertical fences. Finding the largest common distance involves iterating through all horizontal distances and checking for its existence in the vertical distances, which takes O(h^2 * log(v^2)) if a set is used for efficient lookup, or O(h^2 * v^2) with a linear search. Since h+v is proportional to n, the dominant factor is the distance calculation in either horizontal or vertical direction, giving us O(n^2). Therefore the time complexity is O(n^2).

Space Complexity

O(H*H + V*V) – The solution calculates all possible distances between horizontal fences and stores them, resulting in a set of size at most H*H, where H is the number of horizontal fences. Similarly, it stores all possible distances between vertical fences, resulting in a set of size at most V*V, where V is the number of vertical fences. The space used is dominated by storing these distances. Therefore, the overall space complexity is O(H*H + V*V).

Edge Cases

Case	How to Handle
n is zero or negative	Return 0 as the maximum area if the field size is non-positive.
horizontalFences or verticalFences are null or empty	If either fence array is null or empty, the largest possible square has side length 1 (the field boundary), so the area is 1.
horizontalFences or verticalFences contains duplicate fence positions	Convert fence arrays to sets to remove duplicates before processing.
horizontalFences or verticalFences contains values outside the range [0, n]	Filter out any fence positions that are outside the valid range [0, n] inclusive.
No fences are removed. Find largest square area formed by existing fences including the field boundaries (0 and n).	The algorithm should correctly identify the largest square area given the initial fence configuration.
All fences are removed. The largest square area is the entire field, n*n.	The algorithm should calculate the area as n*n when all intermediate fence positions are considered removable.
Integer overflow when calculating the area (side * side)	Use long data type to store side length and area to prevent overflow.
Large input size for horizontalFences or verticalFences leading to performance issues.	Employ an efficient algorithm using sorted sets or lists and binary search for gap determination to maintain reasonable time complexity.