Maximum Students Taking Exam
Hard
1 view
Topics:
ArraysDynamic ProgrammingBit Manipulation
Given a m * n matrix seats that represent seats distributions in a classroom. If a seat is broken, it is denoted by '#' character otherwise it is denoted by a '.' character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the maximum number of students that can take the exam together without any cheating being possible.
Students must be placed in seats in good condition.
Example 1:
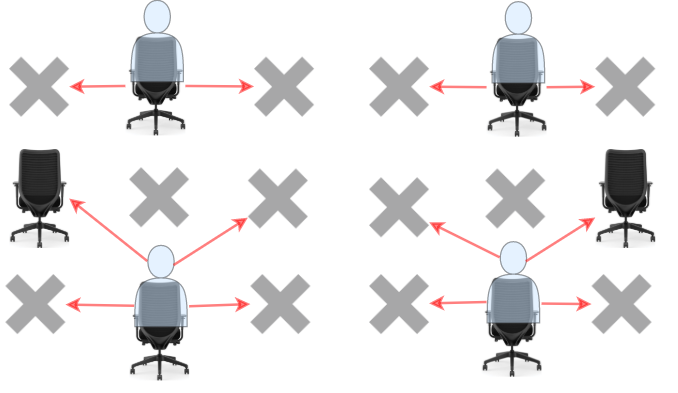
Input: seats = [["#",".","#","#",".","#"], [".","#","#","#","#","."], ["#",".","#","#",".","#"]] Output: 4 Explanation: Teacher can place 4 students in available seats so they don't cheat on the exam.
Example 2:
Input: seats = [[".","#"], ["#","#"], ["#","."], ["#","#"], [".","#"]] Output: 3 Explanation: Place all students in available seats.
Example 3:
Input: seats = [["#",".",".",".","#"], [".","#",".","#","."], [".",".","#",".","."], [".","#",".","#","."], ["#",".",".",".","#"]] Output: 10 Explanation: Place students in available seats in column 1, 3 and 5.
Constraints:
seatscontains only characters'.' and'#'.m == seats.lengthn == seats[i].length1 <= m <= 81 <= n <= 8
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the `seats` array (number of rows and columns), and what is the maximum size of each dimension?
- What are the possible values in the `seats` array? Is it guaranteed to only contain '.' (empty) and '#' (broken) characters?
- If no students can be seated without cheating, what value should I return?
- Are there any restrictions on the number of students I can seat in a row (e.g., at most one student per row)? Or can I fill a row entirely with students if possible?
- Can I assume the input 'seats' array is well-formed (e.g., rectangular, contains only valid characters)? Or do I need to validate the input?
Brute Force Solution
Approach
The brute force method for this problem involves checking every single possible arrangement of students in the classroom. We're essentially trying all combinations of which seats are occupied, and seeing if any of them are valid. We then pick the valid arrangement with the most students.
Here's how the algorithm would work step-by-step:
- Consider each seat in the classroom, one at a time.
- For each seat, try two possibilities: either a student sits there, or no student sits there.
- For every possible arrangement of students sitting or not sitting, check to see if any students are sitting next to each other or diagonally to each other. If so, this arrangement is invalid.
- If the arrangement is valid (no students are sitting illegally), count how many students are sitting in total.
- Repeat this process for every possible combination of students sitting or not sitting in each seat.
- After checking all combinations, find the arrangement with the highest number of students that follows the seating rules.
Code Implementation
def max_students_brute_force(seats):
rows = len(seats)
cols = len(seats[0])
max_students = 0
# Iterate through all possible arrangements
for arrangement_number in range(2**(rows * cols)):
classroom = [['.' for _ in range(cols)] for _ in range(rows)]
student_count = 0
arrangement_string = bin(arrangement_number)[2:].zfill(rows * cols)
index = 0
for row in range(rows):
for col in range(cols):
if arrangement_string[index] == '1':
classroom[row][col] = '#'
student_count += 1
index += 1
is_valid = True
# Check for invalid arrangements
for row in range(rows):
for col in range(cols):
if classroom[row][col] == '#':
# Check adjacent seats
if col > 0 and classroom[row][col-1] == '#':
is_valid = False
break
if col < cols - 1 and classroom[row][col+1] == '#':
is_valid = False
break
# Check diagonal seats
if row > 0 and col > 0 and classroom[row-1][col-1] == '#':
is_valid = False
break
if row > 0 and col < cols - 1 and classroom[row-1][col+1] == '#':
is_valid = False
break
if row < rows - 1 and col > 0 and classroom[row+1][col-1] == '#':
is_valid = False
break
if row < rows - 1 and col < cols - 1 and classroom[row+1][col+1] == '#':
is_valid = False
break
if not is_valid:
break
# Update maximum if valid and better
if is_valid:
# Only update if valid
max_students = max(max_students, student_count)
return max_studentsBig(O) Analysis
Time Complexity
O(2^(m*n)) – The brute force method considers every possible arrangement of students in the classroom. If the classroom has m rows and n columns, there are m*n total seats. For each seat, there are two possibilities: either a student sits there, or no student sits there. Thus, we have 2^(m*n) possible arrangements. For each arrangement, we need to check if it is valid, which takes O(m*n) time in the worst case. Hence, the overall time complexity is O(2^(m*n) * (m*n)), but we drop the (m*n) since the exponential part dominates, resulting in O(2^(m*n)).
Space Complexity
O(1) – The brute force approach, as described, doesn't explicitly use auxiliary data structures like arrays, lists, or hash maps to store intermediate results. It explores all possible combinations by iterating and checking the validity of each arrangement. The space required to store variables for loop counters or temporary variables during the validity check remains constant regardless of the size of the classroom (N, representing the total number of seats). Therefore, the auxiliary space complexity is O(1).
Optimal Solution
Approach
This problem is tricky because we can't just try every single arrangement of students. The key is to think of each row as a binary number and use something called dynamic programming, along with bit masking, to cleverly explore possible seating arrangements row by row, figuring out the best arrangement for each row based on the rows above it.
Here's how the algorithm would work step-by-step:
- First, represent each row of seats as a binary number, where a '1' means the seat is broken and can't be used.
- Then, for each row, figure out all the possible valid ways students can sit, making sure they don't sit next to each other.
- Now, use a technique that remembers past results to build up the best solution. Start with the first row and calculate the maximum number of students you can seat.
- Move to the next row. For each possible valid arrangement of students in this row, check it against all possible valid arrangements of the previous row to make sure students aren't sitting diagonally next to each other.
- Keep track of the best (maximum) number of students we can seat up to this row, given each possible arrangement of students in the current row.
- Repeat this process for all rows. The maximum number of students you've kept track of will be your answer.
Code Implementation
def max_students(seats): rows = len(seats)
cols = len(seats[0])
# Convert rows to integers representing broken seats
classroom_rows = [int(''.join(['1' if seat == '#' else '0' for seat in row]), 2) for row in seats]
all_possible_arrangements = {}
def get_valid_arrangements(number_of_columns): if number_of_columns in all_possible_arrangements:
return all_possible_arrangements[number_of_columns]
valid_arrangements = []
for arrangement in range(1 << number_of_columns):
if arrangement & (arrangement << 1) == 0:
valid_arrangements.append(arrangement)
all_possible_arrangements[number_of_columns] = valid_arrangements
return valid_arrangements
valid_arrangements_per_row = [get_valid_arrangements(cols) for _ in range(rows)]
# dp[i][arrangement] is the max students for rows 0..i ending with arrangement in row i
dp = {}
# Initialize base case for the first row.
for arrangement in valid_arrangements_per_row[0]:
if (classroom_rows[0] & arrangement) == 0:
dp[(0, arrangement)] = bin(arrangement).count('1')
for row_index in range(1, rows):
for current_arrangement in valid_arrangements_per_row[row_index]:
if (classroom_rows[row_index] & current_arrangement) != 0:
continue
for previous_arrangement in valid_arrangements_per_row[row_index - 1]:
# Ensure no diagonal adjacencies.
if (current_arrangement & (previous_arrangement << 1)) != 0 or \
(current_arrangement & (previous_arrangement >> 1)) != 0:
continue
current_count = bin(current_arrangement).count('1')
#Calculate max students given previous arrangements
if (row_index - 1, previous_arrangement) in dp:
previous_max = dp[(row_index - 1, previous_arrangement)]
dp[(row_index, current_arrangement)] = max(dp.get((row_index, current_arrangement), 0), previous_max + current_count)
if not dp:
return 0
# Return the maximum number of students.
return max(dp.values())Big(O) Analysis
Time Complexity
O(m * 2^(2*n)) – Let m be the number of rows and n be the number of seats in each row. Representing each row as a binary number means there are 2^n possible arrangements for each row. We iterate through each row (m rows). For each row, we consider all possible valid arrangements (up to 2^n). When considering a row, we compare its valid arrangements to all valid arrangements of the previous row to check for diagonal adjacency. This comparison takes up to 2^n * 2^n, or 2^(2*n) operations. Therefore, the total time complexity is approximately m * 2^(2*n).
Space Complexity
O(m * 2^m) – The dominant space complexity stems from the dynamic programming approach used to store intermediate results. We need to remember the best arrangements of students up to each row. Since each row can have 'm' seats, and each seat can either be occupied or empty, there are 2^m possible seating arrangements for a row. The dynamic programming table stores the maximum number of students we can seat up to the current row, given each possible arrangement in the current row, for all possible arrangements in the previous row, which can be represented using bitmasking. Therefore, we need to store the results for each row based on the previous row's arrangement, leading to a space complexity of O(m * 2^m), where 'm' is the number of columns in the seats array, since we consider storing m possible values for 2^m states.
Edge Cases
| Case | How to Handle |
|---|---|
| Empty seats array | If the seats array is empty, return 0 as no students can take the exam. |
| Seats array with only one row | Handle a single row by checking if there are any valid seating arrangements for that row only, handling blocked seats correctly. |
| Seats array with only one column | Handle a single column by checking each seat individually, skipping blocked ones. |
| All seats are blocked | If all seats are blocked, the maximum number of students is 0; return 0 immediately. |
| All seats are available | Calculate the maximum students by considering the constraints of adjacent students based on the number of available seats per row. |
| Maximum sized input (large seats array) | Ensure the solution scales efficiently, potentially using dynamic programming with bitmasking to avoid exceeding time or memory limits. |
| Input containing only '.' or only 'x' characters | The solution should correctly process rows with all available seats or all blocked seats. |
| Duplicate row configurations | The dynamic programming approach should inherently handle duplicate row configurations correctly by storing the results of each state. |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
