Maximum Sum BST in Binary Tree
HardGiven a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:

Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6] Output: 20 Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.
Example 2:
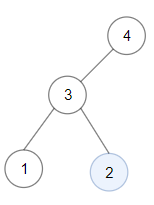
Input: root = [4,3,null,1,2] Output: 2 Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.
Example 3:
Input: root = [-4,-2,-5] Output: 0 Explanation: All values are negatives. Return an empty BST.
Constraints:
- The number of nodes in the tree is in the range
[1, 4 * 104]. -4 * 104 <= Node.val <= 4 * 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that a node in the binary tree can hold? Can nodes contain negative values, zero, or only positive integers?
- What should be returned if the tree is empty, or if no subtree is a valid BST?
- Are there any constraints on the structure of the binary tree (e.g., is it balanced, complete, or is there any limit to its height)?
- By 'maximum sum', do you mean to maximize the sum of the nodes within *one* BST subtree, or across multiple disjoint BST subtrees?
- Is the binary tree guaranteed to be a valid binary tree (no cycles, etc.)?
Brute Force Solution
Approach
The brute force approach to finding the maximum sum BST within a binary tree involves examining every possible subtree. We treat each node as the root of a potential BST and then check if it actually is a valid BST. Finally, we compare the sums of all valid BSTs and choose the largest.
Here's how the algorithm would work step-by-step:
- Consider each node in the tree as the root of a potential Binary Search Tree (BST).
- For each of these potential BSTs, verify if it actually follows the rules of a BST (smaller values on the left, larger values on the right).
- If a potential BST is indeed a valid BST, calculate the sum of all its node values.
- Keep track of the largest sum you've found so far from all the valid BSTs.
- Once you've checked every node as a potential root, the largest sum you've tracked is your answer.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
class Solution:
def maxSumBST(self, root):
maximum_sum = 0
def is_bst(root_node, minimum_value, maximum_value):
if not root_node:
return True
if root_node.value <= minimum_value or root_node.value >= maximum_value:
return False
return is_bst(root_node.left, minimum_value, root_node.value) and \
is_bst(root_node.right, root_node.value, maximum_value)
def tree_sum(root_node):
if not root_node:
return 0
return root_node.value + tree_sum(root_node.left) + tree_sum(root_node.right)
def traverse(root_node):
nonlocal maximum_sum
if not root_node:
return
# Check if the current node is the root of a BST
if is_bst(root_node, float('-inf'), float('inf')):
current_sum = tree_sum(root_node)
# Update maximum sum if the current BST has a larger sum
maximum_sum = max(maximum_sum, current_sum)
traverse(root_node.left)
traverse(root_node.right)
# Iterate through each node in the tree
traverse(root)
return maximum_sumBig(O) Analysis
Optimal Solution
Approach
The most efficient way to solve this problem involves figuring out what information each part of the tree needs to know about its children to make the best decision. We'll use a technique where each part of the tree communicates essential details to its parent, allowing us to work from the bottom up and avoid repeating calculations.
Here's how the algorithm would work step-by-step:
- Start by looking at the smallest parts of the tree, the leaves (nodes at the very bottom).
- For each leaf, determine if it's a valid Binary Search Tree (BST) by itself. Since a single node is always a valid BST, record its value as the maximum BST sum seen so far.
- Move upwards, analyzing each node. For a node to be the root of a valid BST, its left child needs to be a BST, its right child needs to be a BST, its value must be greater than the largest value in the left subtree, and its value must be smaller than the smallest value in the right subtree.
- If a node is the root of a valid BST, calculate the sum of all the nodes in that BST (the node itself plus the sums from its left and right subtrees).
- If the sum of this BST is larger than the largest BST sum we've found so far, update our record of the maximum BST sum.
- As we move up the tree, each node passes information to its parent: whether it is a valid BST, the largest value in its subtree, the smallest value in its subtree, and the sum of its subtree (if it's a valid BST). This avoids recalculating these values at each level.
- Continue this process until you reach the root of the entire tree. The maximum BST sum you've recorded along the way is the answer.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def maxSumBST(self, root: TreeNode) -> int:
max_bst_sum = 0
def traverse(node: TreeNode):
nonlocal max_bst_sum
if not node:
return True, float('inf'), float('-inf'), 0
# Get info from children
is_bst_left, min_left, max_left, sum_left = traverse(node.left)
is_bst_right, min_right, max_right, sum_right = traverse(node.right)
# Node is BST if both subtrees are BSTs
is_bst = (is_bst_left and is_bst_right and
node.val > max_left and node.val < min_right)
if is_bst:
current_sum = node.val + sum_left + sum_right
# Update maximum sum if necessary
max_bst_sum = max(max_bst_sum, current_sum)
# Pass info to the parent
return True, min(node.val, min_left), max(node.val, max_right), current_sum
# If node is not a BST, return False
return False, float('-inf'), float('inf'), 0
traverse(root)
return max_bst_sumBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or Empty Tree | Return 0 immediately, as an empty tree has no BST and thus a sum of 0. |
| Single Node Tree | Return the node's value if it is a valid BST (which it always is in this case). |
| Tree with all negative values | The largest BST sum might be a single node with the least negative value, handled by recursive traversal. |
| Tree with all identical values | The algorithm should correctly identify subtrees that violate BST property and disregard them. |
| Skewed Tree (e.g., left-leaning or right-leaning) | Recursively traverse the tree, exploring all potential BST subtrees regardless of the tree's shape. |
| Integer Overflow of sum | Use a larger data type (e.g., long) to store the sums to prevent overflow. |
| Maximum Depth of Recursion | Ensure the tree does not exceed reasonable recursion depth, potentially using iterative approach for very deep trees. |
| Root node is not part of the maximum sum BST | The recursive solution explores all possible subtrees, guaranteeing the correct maximum is found. |