Maximum Sum of an Hourglass #11 Most Asked
MediumYou are given an m x n integer matrix grid.
We define an hourglass as a part of the matrix with the following form:

Return the maximum sum of the elements of an hourglass.
Note that an hourglass cannot be rotated and must be entirely contained within the matrix.
Example 1:
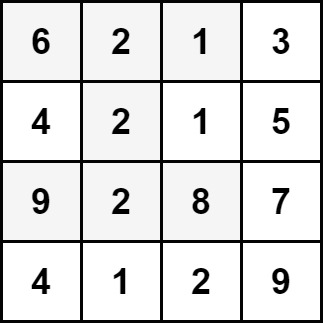
Input: grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]] Output: 30 Explanation: The cells shown above represent the hourglass with the maximum sum: 6 + 2 + 1 + 2 + 9 + 2 + 8 = 30.
Example 2:
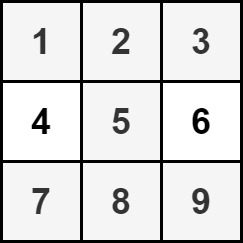
Input: grid = [[1,2,3],[4,5,6],[7,8,9]] Output: 35 Explanation: There is only one hourglass in the matrix, with the sum: 1 + 2 + 3 + 5 + 7 + 8 + 9 = 35.
Constraints:
m == grid.lengthn == grid[i].length3 <= m, n <= 1500 <= grid[i][j] <= 106
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions (rows and columns) of the grid, and what are the constraints on these dimensions? Specifically, what is the minimum size of the grid?
- What is the range of integer values within the grid? Can they be negative, zero, or only positive?
- If the grid dimensions are such that no valid hourglass can be formed (e.g., less than 3 rows or 3 columns), what value should I return?
- Is the input grid guaranteed to be a rectangular 2D array, or could it be jagged (rows with differing lengths)?
- Are we looking for the single maximum hourglass sum, or should I handle potential ties in maximum sums (e.g., returning all hourglasses with the maximum sum, if required)?
Brute Force Solution
Approach
We're trying to find the biggest hourglass shape within a grid of numbers. The brute force method involves looking at every possible place where an hourglass could fit and calculating its sum.
Here's how the algorithm would work step-by-step:
- Imagine sliding an hourglass-shaped cookie cutter across the entire grid.
- At each location where the cookie cutter fits entirely within the grid, calculate the sum of the numbers within the hourglass shape.
- Remember the sum you calculated for each position of the cookie cutter.
- Once you've moved the cookie cutter across the entire grid and calculated the sum for every possible hourglass location, compare all the sums you remembered.
- The largest of these sums is the maximum hourglass sum.
Code Implementation
def max_hourglass_sum_brute_force(grid):
number_of_rows = len(grid)
number_of_columns = len(grid[0]) if number_of_rows > 0 else 0
if number_of_rows < 3 or number_of_columns < 3:
return -1
max_hourglass_sum = float('-inf')
# Iterate through the grid to find possible hourglass locations
for row_index in range(number_of_rows - 2):
for column_index in range(number_of_columns - 2):
# Calculate the sum of the current hourglass
current_hourglass_sum = (
grid[row_index][column_index] +
grid[row_index][column_index + 1] +
grid[row_index][column_index + 2] +
grid[row_index + 1][column_index + 1] +
grid[row_index + 2][column_index] +
grid[row_index + 2][column_index + 1] +
grid[row_index + 2][column_index + 2]
)
# Update the maximum sum if needed
if current_hourglass_sum > max_hourglass_sum:
max_hourglass_sum = current_hourglass_sum
return max_hourglass_sum
Big(O) Analysis
Optimal Solution
Approach
The most efficient way to find the largest hourglass sum involves sliding the hourglass shape across the grid. We calculate the sum for each possible hourglass position and keep track of the highest sum encountered. This avoids redundant calculations by reusing parts of previously computed sums.
Here's how the algorithm would work step-by-step:
- Imagine an hourglass shape sitting on top of the grid.
- Calculate the sum of all the numbers within the hourglass shape.
- Move the hourglass one position to the right. If you can't move right anymore, move it one position down and start from the left again.
- Calculate the sum of the numbers in this new position. You can do this quickly by adding the new numbers and subtracting the old numbers that have shifted out of the hourglass.
- Compare the new sum to the largest sum you've seen so far. If the new sum is bigger, remember it.
- Keep moving the hourglass and repeating the process until you've covered every possible position in the grid.
- The largest sum you remembered is the maximum hourglass sum.
Code Implementation
def find_maximum_hourglass_sum(grid):
rows = len(grid)
columns = len(grid[0])
if rows < 3 or columns < 3:
return -1
maximum_hourglass_sum = float('-inf')
for row_index in range(rows - 2):
for column_index in range(columns - 2):
# Calculate the sum of the current hourglass
current_hourglass_sum = (
grid[row_index][column_index] +
grid[row_index][column_index+1] +
grid[row_index][column_index+2] +
grid[row_index+1][column_index+1] +
grid[row_index+2][column_index] +
grid[row_index+2][column_index+1] +
grid[row_index+2][column_index+2]
)
# Update the maximum sum if necessary
if current_hourglass_sum > maximum_hourglass_sum:
maximum_hourglass_sum = current_hourglass_sum
return maximum_hourglass_sum
def main():
grid = [[1, 1, 1, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 0],
[0, 0, 2, 4, 4, 0],
[0, 0, 0, 2, 0, 0],
[0, 0, 1, 2, 4, 0]]
result = find_maximum_hourglass_sum(grid)
print(result)
if __name__ == "__main__":
main()
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or Empty Grid | Return 0 or throw an exception if the grid is null or empty, as no hourglass can be formed. |
| Grid dimensions too small (rows < 3 or columns < 3) | Return 0 as an hourglass requires at least 3 rows and 3 columns. |
| Grid with all negative numbers | The algorithm should correctly identify the hourglass with the least negative sum as the 'maximum'. |
| Grid with all zero values | The algorithm should return 0, as all hourglass sums will be zero. |
| Grid with large positive numbers that could cause integer overflow when summing hourglass values | Use a larger data type (e.g., long) to store the hourglass sums to prevent potential overflow. |
| Grid with extremely large dimensions (approaching memory limits) | The algorithm should be efficient enough to avoid excessive memory usage; a naive solution that copies large subgrids should be avoided. |
| Grid where the maximum hourglass sum occurs at the top-left or bottom-right corner | Ensure the iteration logic correctly handles hourglasses at the boundaries of the grid without going out of bounds. |
| Grid containing a mix of very large positive and very large negative numbers that cancel each other out | The algorithm should correctly handle this situation and identify the appropriate maximum sum, even if intermediate sums are close to zero. |