Maximum Width of Binary Tree
MediumGiven the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Example 1:
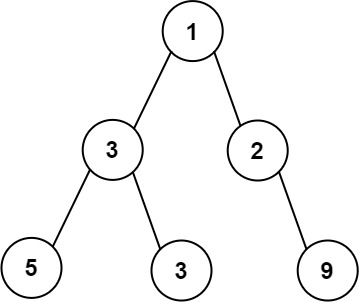
Input: root = [1,3,2,5,3,null,9] Output: 4 Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2:
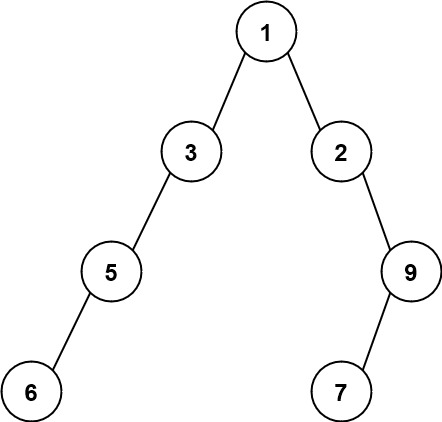
Input: root = [1,3,2,5,null,null,9,6,null,7] Output: 7 Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
Example 3:
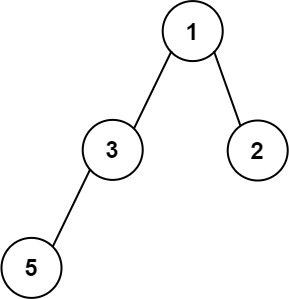
Input: root = [1,3,2,5] Output: 2 Explanation: The maximum width exists in the second level with length 2 (3,2).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the binary tree? Can they be negative?
- Is the tree guaranteed to be a complete binary tree, or are there missing nodes at any level?
- If the tree is empty (null root), should I return 0?
- Are we looking for the maximum width across all levels, or is there a specific level I should be focusing on?
- By 'width', do we count null nodes that are present between two non-null nodes on a level, or only the non-null nodes?
Brute Force Solution
Approach
The brute force way to find the maximum width of a binary tree involves exploring every possible arrangement of nodes at each level. We will calculate the width for each arrangement and then find the largest width across all levels and arrangements. This is done by completely examining all possibilities to identify the largest width.
Here's how the algorithm would work step-by-step:
- First, go through the tree level by level, one level at a time.
- For each level, consider every possible arrangement of the nodes. Pretend there's unlimited space and each node could shift left or right.
- Calculate the width of the level for each of these arrangements. The width is the distance between the leftmost and rightmost node at that level.
- Keep track of the maximum width seen so far at each level.
- After checking all levels and all possible arrangements within those levels, compare the maximum widths found at each level.
- The largest of these level maximums is the maximum width of the entire tree.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def maximum_width_brute_force(root):
if not root:
return 0
maximum_width = 0
queue = [(root, 0, 0)] # (node, level, position)
level_data = {}
while queue:
node, level, position = queue.pop(0)
if level not in level_data:
level_data[level] = []
level_data[level].append(position)
if node.left:
queue.append((node.left, level + 1, position * 2))
if node.right:
queue.append((node.right, level + 1, position * 2 + 1))
#Calculate the width at each level.
for level in level_data:
positions = level_data[level]
level_width = max(positions) - min(positions) + 1
maximum_width = max(maximum_width, level_width)
#The width of the last level is always the maximum
return maximum_widthBig(O) Analysis
Optimal Solution
Approach
To find the maximum width of a binary tree efficiently, we assign a position number to each node as if the tree were a complete binary tree. Then, at each level, the width is simply the difference between the largest and smallest position numbers plus one.
Here's how the algorithm would work step-by-step:
- Imagine the tree is a complete binary tree. The root is at position 1.
- For any node at position 'p', its left child is at position '2*p' and its right child is at position '2*p + 1'.
- Do a level-by-level traversal of the tree. For each level, keep track of the smallest and largest positions of the nodes at that level.
- The width of each level is the largest position minus the smallest position, plus one.
- Keep track of the maximum width found across all levels.
- The maximum width is your final answer.
Code Implementation
from collections import deque
def widthOfBinaryTree(root):
if not root:
return 0
maximum_width = 0
queue = deque([(root, 1)])
while queue:
level_length = len(queue)
# Get the position of the first node in the level
leftmost_position = queue[0][1]
rightmost_position = 0
for _ in range(level_length):
node, position = queue.popleft()
rightmost_position = position
if node.left:
queue.append((node.left, 2 * position))
if node.right:
queue.append((node.right, 2 * position + 1))
# Calculate level width; avoids integer overflow
level_width = rightmost_position - leftmost_position + 1
# Update maximum width
maximum_width = max(maximum_width, level_width)
return maximum_widthBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree | Return 0, as an empty tree has no width. |
| Tree with only one node (root) | Return 1, as the width of a single-node tree is 1. |
| Completely skewed tree (left or right) | The algorithm should correctly traverse the tree and update maximum width for each level; skewed trees are a special case of a general tree and the algorithm should naturally handle them. |
| Complete binary tree | The algorithm should accurately calculate the width based on the numbering scheme and the maximum width will occur on the last level. |
| Tree with large number of nodes (potential integer overflow in indexing) | Use long type for node indexing to prevent potential integer overflow when calculating the width between leftmost and rightmost nodes. |
| Tree where nodes have same extreme value (e.g., Integer.MAX_VALUE) | Node values do not affect the width calculation; only the structure matters. |
| Perfectly balanced tree | The algorithm should calculate maximum width as 2^(height), where height is tree's height. |
| Integer overflow in width calculation | Use long to store intermediate width results to prevent overflow when calculating the difference between leftmost and rightmost indices. |