Merge Two Binary Trees #6 Most Asked
EasyYou are given two binary trees root1 and root2.
Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.
Return the merged tree.
Note: The merging process must start from the root nodes of both trees.
Example 1:
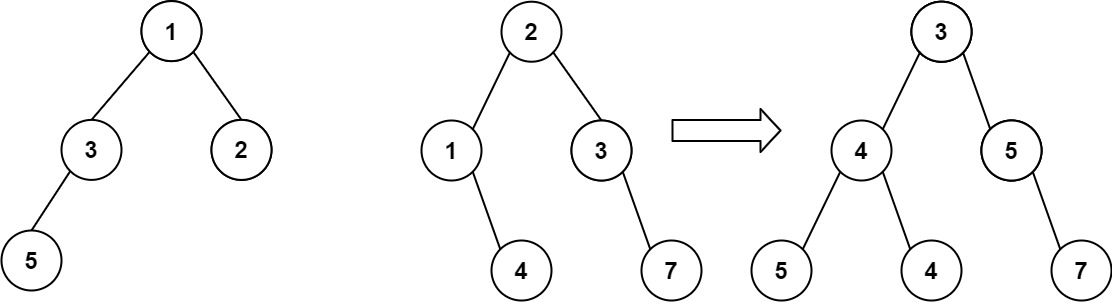
Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] Output: [3,4,5,5,4,null,7]
Example 2:
Input: root1 = [1], root2 = [1,2] Output: [2,2]
Constraints:
- The number of nodes in both trees is in the range
[0, 2000]. -104 <= Node.val <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the expected range of values for the node data in both trees?
- Can either root1 or root2 be null?
- If one tree is significantly larger than the other, should I optimize for that?
- Is it acceptable to modify the existing trees, or do I need to create a completely new tree?
- Are the tree structures guaranteed to be valid binary trees?
Brute Force Solution
Approach
The brute force way to combine two trees is to explore every possible combination of their nodes. We essentially check all pairings of nodes at corresponding positions in the trees and create a new tree based on each combination. This involves exploring all possibilities, leading to a lot of redundant work.
Here's how the algorithm would work step-by-step:
- Look at the very top nodes (roots) of both trees.
- If both trees have a top node, combine their values to create the top node of a new tree.
- If only one tree has a top node, use that node as is for the new tree.
- Now, look at the nodes directly below the top nodes in both original trees (their children).
- Repeat the same process: if both children exist in corresponding positions, combine them; if only one exists, use it directly; if neither exist, there's nothing to add.
- Keep going down the trees, level by level, until you've considered every single node in both trees.
- This means trying every possible combination of nodes at each level to build the merged tree.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def merge_trees_brute_force(root1, root2):
if not root1 and not root2:
return None
# If only one node exists, use that one
if not root1:
return root2
if not root2:
return root1
# Combine the values of the nodes
merged_root_node = TreeNode(root1.val + root2.val)
# Recursively merge the left subtrees
merged_root_node.left = merge_trees_brute_force(root1.left, root2.left)
# Recursively merge the right subtrees
merged_root_node.right = merge_trees_brute_force(root1.right, root2.right)
return merged_root_node
Big(O) Analysis
Optimal Solution
Approach
The most efficient way to merge two trees is to combine them directly as we go, instead of creating a brand new tree. We'll walk through both trees at the same time, deciding how to combine the nodes as we visit them.
Here's how the algorithm would work step-by-step:
- Start by looking at the top nodes (the roots) of both trees.
- If one of the trees is missing a node at a certain spot, just take the node from the other tree.
- If both trees have a node at the same spot, add their values together to create a new node with the combined value.
- Repeat this process for the left and right 'branches' of the trees, going deeper and deeper until you've covered all the nodes.
- By doing this directly, we are modifying the original trees to merge them, or creating a new tree by combining parts from both, which saves time and effort.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def merge_trees(root1, root2):
# If either tree is empty, return the other tree
if not root1:
return root2
if not root2:
return root1
# Combine the values of the current nodes
root1.val += root2.val
# Recursively merge the left subtrees
root1.left = merge_trees(root1.left, root2.left)
# Recursively merge the right subtrees
root1.right = merge_trees(root1.right, root2.right)
return root1Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Both input trees are null | Return null, indicating an empty merged tree. |
| One tree is null, the other is not | Return the non-null tree as the merged tree. |
| Large, unbalanced trees (highly skewed) | The solution should handle potentially deep recursion stacks or, if iterative, large queues. |
| Trees with negative node values | The solution should correctly handle negative values during node value summation. |
| Trees with node values close to integer limits (Integer.MAX_VALUE, Integer.MIN_VALUE) | The solution should guard against potential integer overflow during node value summation. |
| Trees with identical structure and values. | The solution merges correctly by summing the identical values. |
| One tree is much larger than the other. | The solution processes the larger tree correctly, using nodes from it directly when no corresponding node exists in the smaller tree. |
| Trees with only a root node each | Sum root values and return a single node merged tree. |