Minesweeper #10 Most Asked
MediumLet's play the minesweeper game (Wikipedia, online game)!
You are given an m x n char matrix board representing the game board where:
'M'represents an unrevealed mine,'E'represents an unrevealed empty square,'B'represents a revealed blank square that has no adjacent mines (i.e., above, below, left, right, and all 4 diagonals),- digit (
'1'to'8') represents how many mines are adjacent to this revealed square, and 'X'represents a revealed mine.
You are also given an integer array click where click = [clickr, clickc] represents the next click position among all the unrevealed squares ('M' or 'E').
Return the board after revealing this position according to the following rules:
- If a mine
'M'is revealed, then the game is over. You should change it to'X'. - If an empty square
'E'with no adjacent mines is revealed, then change it to a revealed blank'B'and all of its adjacent unrevealed squares should be revealed recursively. - If an empty square
'E'with at least one adjacent mine is revealed, then change it to a digit ('1'to'8') representing the number of adjacent mines. - Return the board when no more squares will be revealed.
Example 1:
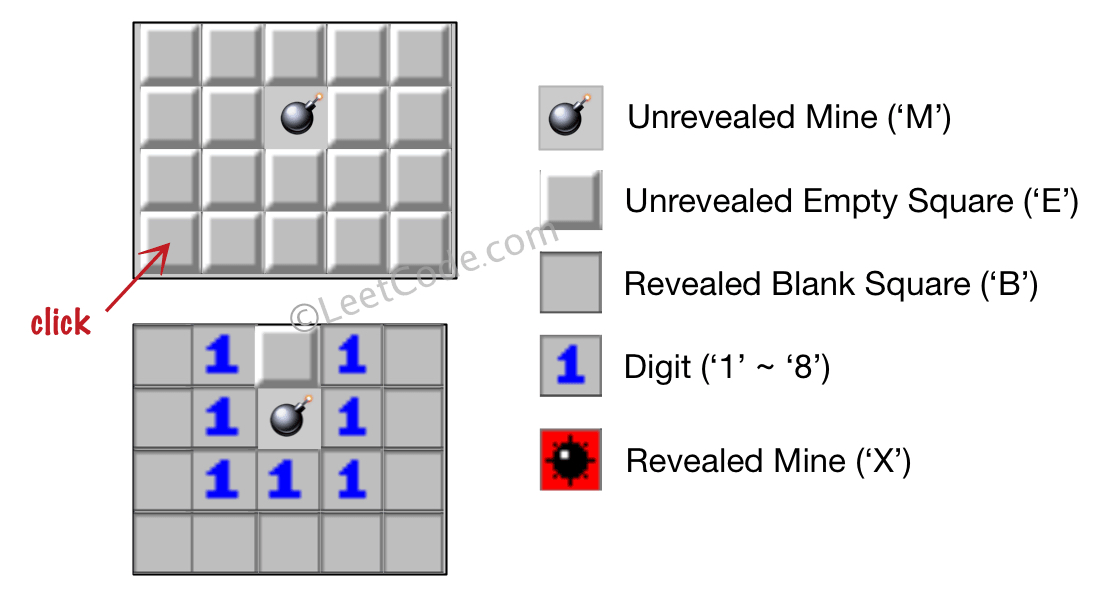
Input: board = [["E","E","E","E","E"],["E","E","M","E","E"],["E","E","E","E","E"],["E","E","E","E","E"]], click = [3,0] Output: [["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]
Example 2:
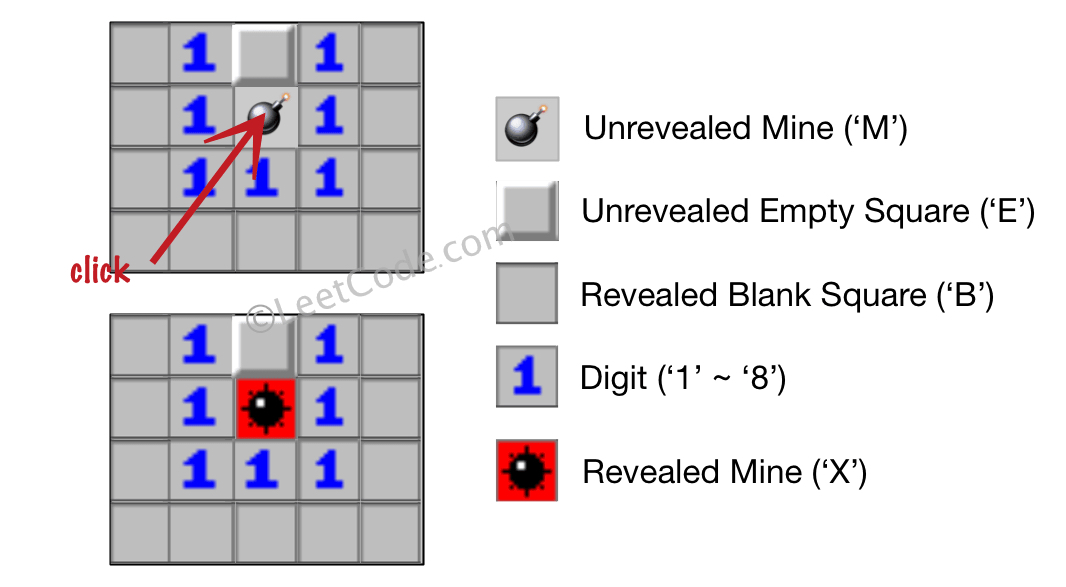
Input: board = [["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]], click = [1,2] Output: [["B","1","E","1","B"],["B","1","X","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]
Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 50board[i][j]is either'M','E','B', or a digit from'1'to'8'.click.length == 20 <= clickr < m0 <= clickc < nboard[clickr][clickc]is either'M'or'E'.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the board, and what is the data type used to represent the board (e.g., 2D array of characters or integers)?
- How are mines represented on the board? Is it a specific character (e.g., 'M') or a numerical value?
- If a cell has no adjacent mines, what value should be placed in that cell (e.g., '0', or an empty space)?
- Are the input coordinates for the click guaranteed to be within the bounds of the board? What should I do if they are out of bounds?
- Is the provided board guaranteed to be valid initially (i.e., does it contain valid mine locations, and are numbers around mines consistent with the mine locations)?
Brute Force Solution
Approach
The minesweeper problem involves figuring out what the board should look like after you reveal a square. The brute force method reveals the given square and then checks every other square, updating the numbers on the board by simply recounting the mines surrounding each one.
Here's how the algorithm would work step-by-step:
- First, reveal the square that the player clicked on.
- Now, go through every single square on the board, one by one.
- For each square, count how many mines are touching it (diagonally, horizontally, and vertically).
- Write down the count of mines next to that square. This is the number that is displayed on the revealed board, if it is not a mine itself.
- If the originally revealed square had no adjacent mines and the game is configured to reveal such squares, recursively repeat the counting and updating for the neighbor squares that are also empty, until there are no more empty neighbors.
Code Implementation
def minesweeper_brute_force(board, row_click, column_click):
rows = len(board)
columns = len(board[0])
# Reveal the clicked square
reveal_square(board, row_click, column_click)
for row_index in range(rows):
for column_index in range(columns):
# Count adjacent mines for each square
count = count_adjacent_mines(board, row_index, column_index)
if board[row_index][column_index] != 'M':
board[row_index][column_index] = str(count) if count > 0 else 'E'
# Recursively reveal empty squares if the clicked square was empty
if board[row_click][column_click] == 'E':
reveal_empty_squares(board, row_click, column_click)
return board
def reveal_square(board, row_index, column_index):
if board[row_index][column_index] == 'M':
board[row_index][column_index] = 'X'
elif board[row_index][column_index] == 'E':
board[row_index][column_index] = 'B'
def count_adjacent_mines(board, row_index, column_index):
rows = len(board)
columns = len(board[0])
mine_count = 0
for i in range(max(0, row_index - 1), min(rows, row_index + 2)):
for j in range(max(0, column_index - 1), min(columns, column_index + 2)):
if (i, j) != (row_index, column_index) and board[i][j] == 'M':
mine_count += 1
return mine_count
def reveal_empty_squares(board, row_index, column_index):
rows = len(board)
columns = len(board[0])
if row_index < 0 or row_index >= rows or column_index < 0 or column_index >= columns or board[row_index][column_index] != 'E':
return
board[row_index][column_index] = 'B'
# Recursively reveal neighboring empty squares
for i in range(max(0, row_index - 1), min(rows, row_index + 2)):
for j in range(max(0, column_index - 1), min(columns, column_index + 2)):
if (i, j) != (row_index, column_index) and board[i][j] == 'E':
# Need to check the adjacent mines for each recursive step
adjacent_mines_count = count_adjacent_mines(board, i, j)
if adjacent_mines_count == 0:
reveal_empty_squares(board, i, j)
else:
board[i][j] = str(adjacent_mines_count)
# This is the base case for recursion, stopping it.Big(O) Analysis
Optimal Solution
Approach
We need to reveal the Minesweeper board based on clicks. The key is to efficiently reveal all safe cells connected to a clicked empty cell. This avoids unnecessary checks and directly reveals large areas at once.
Here's how the algorithm would work step-by-step:
- When the player clicks a cell, first check if it's already revealed or if it contains a mine. If so, stop.
- If the clicked cell is empty (has a mine count of zero), reveal it.
- Next, reveal all adjacent cells. If any of these adjacent cells are also empty, repeat the process for them. This will continue until we hit cells with mine counts greater than zero, or the edge of the board.
- For each adjacent cell that has a mine count greater than zero, reveal just that cell and stop further exploration in that direction.
- If the clicked cell itself has a mine count greater than zero, reveal only that cell and stop. Do not recursively reveal its neighbors.
Code Implementation
def reveal_minesweeper(board, click_row, click_col):
rows = len(board)
cols = len(board[0])
if board[click_row][click_col] == 'M':
board[click_row][click_col] = 'X'
return board
def get_adjacent_mines(row, col):
mine_count = 0
for i in range(max(0, row - 1), min(rows, row + 2)):
for j in range(max(0, col - 1), min(cols, col + 2)):
if i == row and j == col:
continue
if board[i][j] == 'M':
mine_count += 1
return mine_count
def reveal_adjacent_cells(row, col):
if row < 0 or row >= rows or col < 0 or col >= cols or board[row][col] != 'E':
return
adjacent_mines = get_adjacent_mines(row, col)
if adjacent_mines > 0:
board[row][col] = str(adjacent_mines)
return
# Reveals the current cell since it is empty.
board[row][col] = 'B'
# Recursively reveals neighboring cells.
for i in range(max(0, row - 1), min(rows, row + 2)):
for j in range(max(0, col - 1), min(cols, col + 2)):
if i == row and j == col:
continue
reveal_adjacent_cells(i, j)
# Start the revealing process with the initial click.
reveal_adjacent_cells(click_row, click_col)
return boardBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty board input | Return an empty board or throw an exception, depending on the specifications and language conventions. |
| Board with dimensions 1x1 | Check the single cell for a mine and return a 1x1 board with either 'M' replaced by 'X' or a number representing adjacent mines, or 'E' replaced by '0' if no adjacent mines. |
| Board filled entirely with mines | If clicking on a mine, mark it as 'X' and return; otherwise, no changes are needed since there are no safe cells to reveal. |
| Board filled entirely with empty cells ('E') | The algorithm should recursively reveal all connected empty cells and their adjacent number cells. |
| Clicking on a mine ('M') at the edge of the board | The solution should handle edge indices gracefully and mark the mine as 'X' without causing an out-of-bounds error. |
| Clicking on a cell with many adjacent mines (e.g., 8 adjacent mines) | The number of adjacent mines should be calculated correctly even at the maximum value, staying within the valid number representation. |
| Invalid input: row or col coordinate outside the board bounds | Check that the row and col values are within the board's dimensions before accessing board elements, returning the original board if invalid. |
| Integer overflow when calculating adjacent mines count, especially with large board dimensions | Use appropriate data types to store the count of adjacent mines to avoid integer overflow, such as int in most cases. |