Minimum Array Length After Pair Removals
MediumGiven an integer array num sorted in non-decreasing order.
You can perform the following operation any number of times:
- Choose two indices,
iandj, wherenums[i] < nums[j]. - Then, remove the elements at indices
iandjfromnums. The remaining elements retain their original order, and the array is re-indexed.
Return the minimum length of nums after applying the operation zero or more times.
Example 1:
Input: nums = [1,2,3,4]
Output: 0
Explanation:
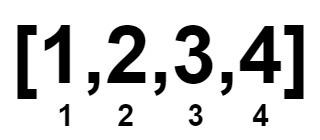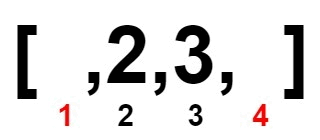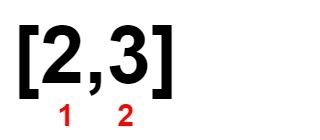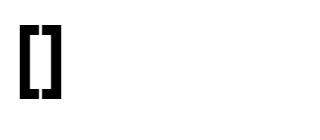
Example 2:
Input: nums = [1,1,2,2,3,3]
Output: 0
Explanation:
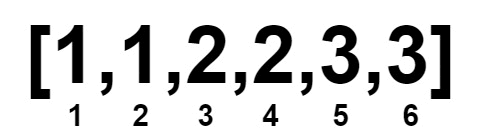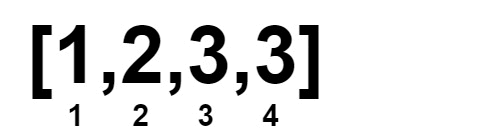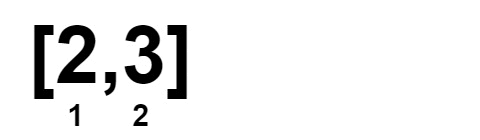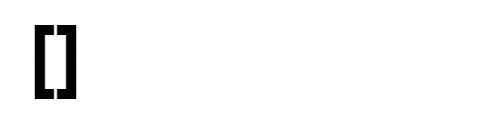
Example 3:
Input: nums = [1000000000,1000000000]
Output: 2
Explanation:
Since both numbers are equal, they cannot be removed.
Example 4:
Input: nums = [2,3,4,4,4]
Output: 1
Explanation:
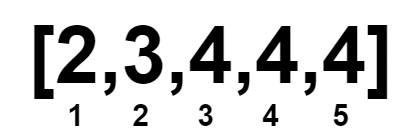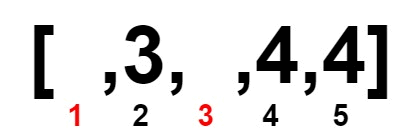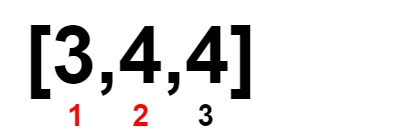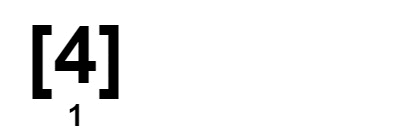
Constraints:
1 <= nums.length <= 1051 <= nums[i] <= 109numsis sorted in non-decreasing order.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the size of the input array `nums`?
- Can the integers in `nums` be negative, zero, or only positive?
- Are there any constraints on the range of values within the `nums` array?
- If the length of the array cannot be reduced by any pair removals, what should I return?
- If multiple pairs could be removed in any given operation, is there a preference as to which pairs are chosen?
Brute Force Solution
Approach
The brute force approach to this problem involves trying every possible combination of removing pairs of equal numbers from the list. We repeatedly remove pairs until no more removals are possible and then count what's left. It is an exhaustive, albeit inefficient, way to guarantee we find the smallest possible resulting list.
Here's how the algorithm would work step-by-step:
- Look at the beginning of the list.
- Find the very first number in your list.
- Now, go through the rest of the list to see if you can find another number that is the same.
- If you find a match, remove both numbers from the list and start over from the beginning with the updated list.
- If you go through the entire list and don't find a matching number for the very first number, move to the second number in the original list and repeat the process looking for matches after that second number.
- Keep repeating this process, considering each number in the list, and looking for matching numbers later in the list to remove.
- Eventually, you will get to a point where you cannot find any more matching pairs to remove.
- At that point, the number of items remaining in the list represents the minimum length you can achieve after removing all possible pairs.
Code Implementation
def minimum_array_length_after_pair_removals_brute_force(collection):
def solve(current_collection):
if not current_collection:
return 0
minimum_length = len(current_collection)
# Try removing every possible pair
for first_index in range(len(current_collection)):
for second_index in range(first_index + 1, len(current_collection)):
if current_collection[first_index] == current_collection[second_index]:
# Create a new collection with the pair removed
new_collection = current_collection[:first_index] + current_collection[first_index+1:second_index] + current_collection[second_index+1:]
# Recursively solve for the new collection
length_after_removal = solve(new_collection)
minimum_length = min(minimum_length, length_after_removal)
# If no pairs can be removed, return the current length
return minimum_length
# Initiate the process and return the minimum array length
return solve(collection)Big(O) Analysis
Optimal Solution
Approach
The problem asks us to remove pairs of identical numbers from a collection. The key idea is to realize that we only care about the most frequent number and how it relates to the total count. If a single number appears more than half the time, it dictates how much we can actually remove.
Here's how the algorithm would work step-by-step:
- First, count how many times each number appears in the collection.
- Identify the number that appears most often.
- Check if the count of the most frequent number is greater than half the size of the entire collection.
- If it is, then the remaining array length is twice the difference between the most frequent number's count and half the collection size. This means after pairing, the most frequent number's excess over half remains, and gets doubled as there is no corresponding partner for these numbers to match with
- If it isn't, then all numbers can be removed by pairs, resulting in an empty array (length 0).
Code Implementation
def min_array_length(numbers):
counts = {}
for number in numbers:
counts[number] = counts.get(number, 0) + 1
most_frequent_count = 0
other_numbers_count = 0
for number, count in counts.items():
if count > most_frequent_count:
most_frequent_count = count
# Sum the counts of all numbers besides the most frequent one.
for number, count in counts.items():
if count != most_frequent_count:
other_numbers_count += count
elif list(counts.values()).count(most_frequent_count) > 1:
other_numbers_count += count
most_frequent_count = most_frequent_count
break
# Determine the remaining array length after pair removals.
if most_frequent_count > other_numbers_count:
return most_frequent_count - other_numbers_count
# When most frequent is less than other numbers, all can be paired.
return (len(numbers) % 2)Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null input array | Return 0 if the input array is null to avoid NullPointerException. |
| Empty array | Return 0 if the input array is empty since there are no elements to remove. |
| Array with only one element | Return 1 as no pair can be formed for removal. |
| Array with two identical elements | Return 0 as they can be removed as a valid pair. |
| Array with two distinct elements | Return 0 as they can be removed as a valid pair. |
| Array with all identical elements and even length | Return 0 as all elements can be paired and removed. |
| Array with all identical elements and odd length | Return 1 as all but one element can be paired and removed. |
| Large array with a single dominant element | Counting the frequency of elements efficiently using a hash map will determine the result depending on whether the dominant element's count is less than or equal to half the array's length. |