Minimum Cost to Move Chips to The Same Position #4 Most Asked
EasyWe have n chips, where the position of the ith chip is position[i].
We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:
position[i] + 2orposition[i] - 2withcost = 0.position[i] + 1orposition[i] - 1withcost = 1.
Return the minimum cost needed to move all the chips to the same position.
Example 1:
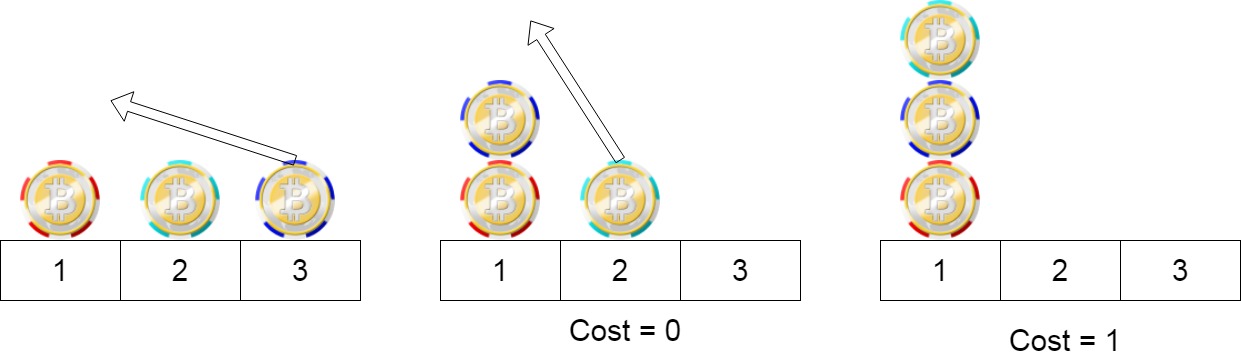
Input: position = [1,2,3] Output: 1 Explanation: First step: Move the chip at position 3 to position 1 with cost = 0. Second step: Move the chip at position 2 to position 1 with cost = 1. Total cost is 1.
Example 2:

Input: position = [2,2,2,3,3] Output: 2 Explanation: We can move the two chips at position 3 to position 2. Each move has cost = 1. The total cost = 2.
Example 3:
Input: position = [1,1000000000] Output: 1
Constraints:
1 <= position.length <= 1001 <= position[i] <= 10^9
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the size of the `positions` array, and the range of values within it?
- Can the values in the `positions` array be negative, zero, or non-integer?
- If the input array is empty or null, what should I return?
- Are there any specific performance considerations or memory constraints I should be aware of, given a very large input array?
- Is there a requirement to return the target position, or just the minimum cost itself?
Brute Force Solution
Approach
The brute force approach tries every possible location to move all the chips to. For each location, we calculate the total cost of moving all chips there and then pick the location with the lowest cost.
Here's how the algorithm would work step-by-step:
- Consider each position as a possible final destination.
- For each possible final destination, calculate the cost to move each chip individually to that destination. Moving a chip one position costs one unit.
- Sum up the cost for moving all chips to that particular destination. This gives you the total cost for that location.
- Repeat this process for every possible final destination.
- Compare the total costs obtained for all the possible destinations.
- Select the destination that resulted in the minimum total cost. That's your answer.
Code Implementation
def min_cost_to_move_chips_brute_force(positions):
minimum_total_cost = float('inf')
# Consider each position as a potential destination
for destination in positions:
total_cost_for_destination = 0
for chip_position in positions:
# Calculate cost to move this chip to destination
cost_to_move = abs(chip_position - destination)
total_cost_for_destination += cost_to_move
# Keep track of the minimum cost seen so far
minimum_total_cost = min(minimum_total_cost, total_cost_for_destination)
return minimum_total_costBig(O) Analysis
Optimal Solution
Approach
The key insight is that moving a chip two positions away costs nothing. Therefore, we only need to consider moving chips either one position away. The optimal solution involves counting how many chips are in even positions and how many are in odd positions and then selecting the smaller count as the answer.
Here's how the algorithm would work step-by-step:
- Separate the chips into two groups: those at even-numbered locations and those at odd-numbered locations.
- Count how many chips are in the even group and how many are in the odd group.
- Choose the smaller of the two counts. This is the minimum cost to move all the chips to the same position.
- The idea is that the chips in the larger group are moved to the position of chips in the smaller group by at most one position away from each other (since even moves are free).
- For example, if there are fewer chips at even locations, we'll move the chips in odd locations to an adjacent even spot. This costs 1 per chip.
Code Implementation
def minimum_cost_to_move_chips(position):
even_position_count = 0
odd_position_count = 0
# Iterate through the positions array
for current_position in position:
# Count positions, even or odd
if current_position % 2 == 0:
even_position_count += 1
else:
odd_position_count += 1
# We pick the minimum between even and odd counts, as we move
# all chips to either all even or all odd positions. The moves between
# the same parity are free
if even_position_count < odd_position_count:
return even_position_count
else:
return odd_position_countBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty input array. | Return 0, as no moves are needed with no chips. |
| Array with a single chip. | Return 0, as the chip is already at a single position. |
| Array with two chips at adjacent positions. | The minimum cost is 0 to move them to the same position (either position). |
| Array with chips at positions differing by a multiple of 2. | Moving chips between these positions involves cost 1 for each move of two positions. |
| All chips are already at the same position. | The minimum cost is 0, as no moves are needed. |
| Array contains a mix of even and odd positions. | Count evens and odds, return the minimum of the two counts. |
| Input array with very large numbers. | The numbers themselves don't matter, only whether they are even or odd, so large numbers do not cause overflow. |
| Input with negative numbers. | Only the parity matters. The problem statement does not specify a range. |