Minimum Cost Tree From Leaf Values #16 Most Asked
MediumGiven an array arr of positive integers, consider all binary trees such that:
- Each node has either
0or2children; - The values of
arrcorrespond to the values of each leaf in an in-order traversal of the tree. - The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.
Among all possible binary trees considered, return the smallest possible sum of the values of each non-leaf node. It is guaranteed this sum fits into a 32-bit integer.
A node is a leaf if and only if it has zero children.
Example 1:
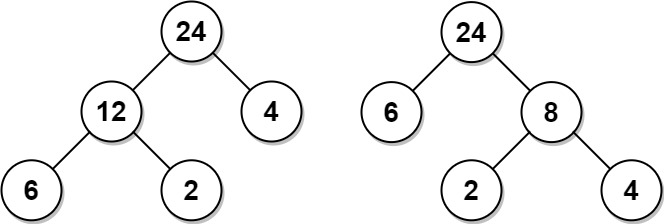
Input: arr = [6,2,4] Output: 32 Explanation: There are two possible trees shown. The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.
Example 2:
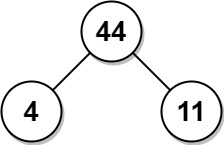
Input: arr = [4,11] Output: 44
Constraints:
2 <= arr.length <= 401 <= arr[i] <= 15- It is guaranteed that the answer fits into a 32-bit signed integer (i.e., it is less than 231).
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum size of the input array `arr`? Specifically, what is the upper bound on the number of leaf nodes?
- Can the input array `arr` contain duplicate values, and if so, how should that affect the construction of the minimum cost tree?
- Is the input array `arr` guaranteed to contain only positive integers, or could it contain zero or negative values?
- If the input array `arr` is empty or contains only one element, what should the function return?
- Could you provide an example of a non-trivial input and the expected output to further clarify the problem's constraints?
Brute Force Solution
Approach
The brute force approach to finding the minimum cost tree from leaf values is like trying out every single possible tree you can make with those leaf values. We calculate the cost for each possible tree and then pick the one with the lowest cost.
Here's how the algorithm would work step-by-step:
- First, consider all possible ways to split the list of leaf values into two smaller lists.
- For each split, calculate the cost of merging those two lists into a single node in the tree. This cost is the product of the largest value in each of the two lists.
- Then, for each of the smaller lists we created, repeat the process: try every possible split of that list into two even smaller lists and calculate the cost of merging those.
- Keep splitting and merging lists until you have individual leaf values. Each merge represents a node in a potential tree.
- For each tree you've built this way, add up all the merging costs you calculated along the way to get the total cost for that tree.
- Finally, compare the total costs of all the possible trees you created and choose the tree with the smallest total cost. That's your minimum cost tree.
Code Implementation
def minimum_cost_tree_from_leaf_values_brute_force(leaf_values):
def calculate_minimum_cost(current_leaf_values):
number_of_leafs = len(current_leaf_values)
if number_of_leafs <= 1:
return 0
minimum_cost = float('inf')
# Try all possible splits of the leaf values.
for i in range(1, number_of_leafs):
left_subtree = current_leaf_values[:i]
right_subtree = current_leaf_values[i:]
# The cost of merging the subtrees is the product of their maximum values.
merging_cost = max(left_subtree) * max(right_subtree)
# Recursively calculate the cost of the subtrees and add them.
left_subtree_cost = calculate_minimum_cost(left_subtree)
right_subtree_cost = calculate_minimum_cost(right_subtree)
total_cost = merging_cost + left_subtree_cost + right_subtree_cost
minimum_cost = min(minimum_cost, total_cost)
return minimum_cost
return calculate_minimum_cost(leaf_values)
Big(O) Analysis
Optimal Solution
Approach
The key is to build the tree from the bottom up. We repeatedly combine the smallest pairs of leaves, calculating the cost of each merge, until we're left with a single root.
Here's how the algorithm would work step-by-step:
- Think of the problem as repeatedly merging pairs of numbers until only one remains.
- At each step, find the smallest adjacent pair of numbers.
- Multiply these two numbers to get the cost of merging them.
- Replace the pair with the larger of the two numbers. This is important: we only keep the larger one because it affects future calculations.
- Add the cost to a running total.
- Repeat steps 2-5 until only one number remains.
- The running total represents the minimum cost to build the tree.
Code Implementation
def minimum_cost_tree_from_leaf_values(leaf_values):
minimum_cost = 0
while len(leaf_values) > 1:
minimum_index = 0
#Find the index of the smallest adjacent pair
for index in range(1, len(leaf_values)):
if leaf_values[index] * leaf_values[index-1] < \
leaf_values[minimum_index] * leaf_values[minimum_index-1]:
minimum_index = index
#Cost is product of the smallest adjacent pair
minimum_cost += leaf_values[minimum_index] * leaf_values[minimum_index - 1]
#Replace pair with larger element
leaf_values[minimum_index-1] = max(leaf_values[minimum_index], leaf_values[minimum_index-1])
#Remove the smaller element
leaf_values.pop(minimum_index)
return minimum_costBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty input array | Return 0 as there are no leaf nodes and thus no non-leaf nodes to sum. |
| Input array with only one element | Return 0 as a single leaf node forms a trivial tree with no non-leaf nodes. |
| Input array with two elements | Return the product of the two elements, which is the only possible cost. |
| Input array with all elements being the same value | The algorithm should still compute the correct minimum cost, as the leaf values are handled uniformly. |
| Input array with elements sorted in increasing order | The algorithm should efficiently explore different tree structures despite the sorted input. |
| Input array with elements sorted in decreasing order | The algorithm should efficiently explore different tree structures despite the reverse-sorted input. |
| Input array with very large integer values leading to potential integer overflow | Use a data type that can accommodate larger products, such as long or consider using modular arithmetic if appropriate and stated by problem. |
| Input array with a large number of elements | Dynamic programming optimization is required to prevent exceeding time limit due to exponential tree growth. |