Minimum Degree of a Connected Trio in a Graph

Hard

GoDaddy

2 views

Topics:

ArraysGraphs

You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [u_i, v_i] indicates that there is an undirected edge between u_i and v_i.

A connected trio is a set of three nodes where there is an edge between every pair of them.

The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.

Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.

Example 1:

Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
Output: 3
Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.

Example 2:

Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
Output: 0
Explanation: There are exactly three trios:
1) [1,4,3] with degree 0.
2) [2,5,6] with degree 2.
3) [5,6,7] with degree 2.

Constraints:

2 <= n <= 400
edges[i].length == 2
1 <= edges.length <= n * (n-1) / 2
1 <= u_i, v_i <= n
u_i!= v_i
There are no repeated edges.

Minimum Degree of a Connected Trio in a Graph

Hard

GoDaddy

2 views

Topics:

ArraysGraphs

You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [u_i, v_i] indicates that there is an undirected edge between u_i and v_i.

A connected trio is a set of three nodes where there is an edge between every pair of them.

The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.

Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.

Example 1:

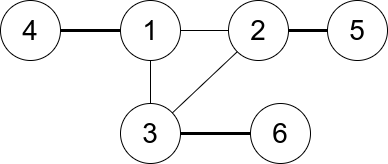
Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
Output: 3
Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.

Example 2:

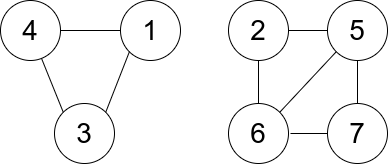
Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
Output: 0
Explanation: There are exactly three trios:
1) [1,4,3] with degree 0.
2) [2,5,6] with degree 2.
3) [5,6,7] with degree 2.

Constraints:

2 <= n <= 400
edges[i].length == 2
1 <= edges.length <= n * (n-1) / 2
1 <= u_i, v_i <= n
u_i!= v_i
There are no repeated edges.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the number of nodes `n` in the graph and the number of edges?
Can the graph be disconnected? Should I return -1 if no connected trio exists?
Are the edges undirected or directed?
Are there any self-loops (edges from a node to itself) or duplicate edges in the input?
Is the input graph represented as an adjacency list, an adjacency matrix, or a list of edges?

Brute Force Solution

Approach

The brute force approach involves checking every possible group of three connected nodes in the graph. For each group, we calculate its 'degree' (number of connections) and keep track of the smallest degree we find. In the end, we return this minimum degree, or a special value if no connected trio exists.

Here's how the algorithm would work step-by-step:

First, look at all possible combinations of three nodes in the graph.
For each combination, check if those three nodes are all connected to each other. In other words, is there a direct link between each pair of nodes?
If the three nodes are indeed connected as a trio, count how many other nodes each of those three nodes is linked to. This count is the degree for each node in the trio.
Add the degrees of the three nodes together to get the total degree of the trio. Then subtract 6 from the total, since the connections between the nodes in the trio were counted twice.
Compare this total degree to the smallest degree found so far. If it's smaller, update the smallest degree.
Repeat this process for every possible combination of three nodes.
If, after checking all combinations, no connected trio was found, return a special value indicating that there are no connected trios. Otherwise, return the smallest degree that was found.

Code Implementation

def minimum_degree_connected_trio(number_of_nodes: int, edges: list[list[int]]) -> int:
    adjacency_matrix = [[False] * (number_of_nodes + 1) for _ in range(number_of_nodes + 1)]
    degrees = [0] * (number_of_nodes + 1)

    for edge in edges:
        node_a, node_b = edge
        adjacency_matrix[node_a][node_b] = True
        adjacency_matrix[node_b][node_a] = True
        degrees[node_a] += 1
        degrees[node_b] += 1

    minimum_trio_degree = float('inf')
    found_trio = False

    # Iterate through all possible combinations of three nodes
    for node_i in range(1, number_of_nodes + 1):
        for node_j in range(node_i + 1, number_of_nodes + 1):
            for node_k in range(node_j + 1, number_of_nodes + 1):

                # Check if all three nodes are connected to each other
                if adjacency_matrix[node_i][node_j] and \
                   adjacency_matrix[node_i][node_k] and \
                   adjacency_matrix[node_j][node_k]:

                    # Calculate the degree of the trio
                    trio_degree = degrees[node_i] + degrees[node_j] + degrees[node_k] - 6

                    # Update the minimum degree if necessary
                    minimum_trio_degree = min(minimum_trio_degree, trio_degree)
                    found_trio = True

    # If no connected trio was found, return -1
    if not found_trio:
        return -1

    return minimum_trio_degree

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n^3) – The algorithm iterates through all possible combinations of three nodes in the graph, where 'n' represents the number of nodes. This involves a triple nested loop structure examining each possible triplet of nodes. For each triplet, we check for connectivity between the three nodes, which takes constant time. Therefore, the dominant factor is the iteration through all possible triplets, leading to a time complexity proportional to n * n * n, which simplifies to O(n^3).

Space Complexity

O(1) – The brute force approach iterates through combinations of nodes and checks for connectivity. It primarily uses a few integer variables to store the current trio of nodes being considered, and the minimum degree found so far. The space used for these variables is constant regardless of the number of nodes (N) or edges in the graph. Therefore, the auxiliary space complexity is O(1).

Optimal Solution

Approach

The problem asks us to find a group of three connected nodes in a graph with the smallest combined degree. Instead of checking every possible group of three, we can be smarter by focusing on existing connections and then checking for the third connection to form a trio. This significantly reduces the work we have to do.

Here's how the algorithm would work step-by-step:

First, we need to represent the graph so we can quickly check if two nodes are connected.
Then, we go through all the connections that exist in the graph one by one.
For each connection, we check if there is a third node that is connected to both nodes in the original connection.
If we find such a third node, we have a trio, and we calculate the combined degree of these three nodes. Remember to subtract 2 for each node since each node is connected to the other two.
We keep track of the smallest combined degree we have found so far.
If we go through all connections and don't find any trio, we return a special value to indicate that no trio exists.

Code Implementation

def minimum_degree_of_connected_trio(number_of_nodes, edges):
    adjacency_matrix = [[False] * (number_of_nodes + 1) for _ in range(number_of_nodes + 1)]
    degrees = [0] * (number_of_nodes + 1)

    for edge_start, edge_end in edges:
        adjacency_matrix[edge_start][edge_end] = True
        adjacency_matrix[edge_end][edge_start] = True
        degrees[edge_start] += 1
        degrees[edge_end] += 1

    minimum_trio_degree = float('inf')

    # Iterate through all possible edge combinations.
    for edge_start, edge_end in edges:

        # Find a third node connected to both ends of the edge.
        for potential_third_node in range(1, number_of_nodes + 1):
            if adjacency_matrix[edge_start][potential_third_node] and adjacency_matrix[edge_end][potential_third_node]:

                # Calculate trio degree, subtracting 2 for connections.
                trio_degree = degrees[edge_start] + degrees[edge_end] + degrees[potential_third_node] - 6
                minimum_trio_degree = min(minimum_trio_degree, trio_degree)

    # No trio found return -1, otherwise return minimum degree
    if minimum_trio_degree == float('inf'):
        return -1
    else:
        return minimum_trio_degree

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(E + n^3) – The algorithm iterates through all edges in the graph which takes O(E) time where E is the number of edges. For each edge (u, v), it iterates through all possible nodes 'w' to check if 'w' is connected to both 'u' and 'v'. Checking if 'w' is connected to both 'u' and 'v' involves two lookups in the adjacency matrix which takes O(1) time. Thus, for each edge, checking all possible 'w' takes O(n) time where n is the number of nodes. Therefore, the nested loop checking for trios contributes a complexity of O(E * n). Since in the worst case E can be proportional to n^2 (dense graph), the overall complexity is O(n^2 * n) which simplifies to O(n^3). In total we get O(E + n^3), which simplifies to O(n^3) when E is significantly smaller than n^3 or O(n^3) otherwise.

Space Complexity

O(N^2) – The primary space complexity arises from representing the graph to quickly check if two nodes are connected. The most common way to do this efficiently is with an adjacency matrix, which requires a boolean array of size N x N, where N is the number of nodes in the graph. The algorithm also uses a few integer variables to store the minimum degree and loop counters, which take constant space. Therefore, the overall auxiliary space complexity is dominated by the adjacency matrix, resulting in O(N^2).

Edge Cases

Case	How to Handle
Empty graph (n=0)	Return -1 immediately since no trio can exist in an empty graph.
Graph with fewer than 3 nodes (n < 3)	Return -1 immediately since a trio requires at least 3 nodes.
No edges present in the graph	Return -1 as no connected trio can exist without any edges.
Complete graph where every node is connected to every other node	The minimum degree will be easily calculable as each trio will have degree 3.
Graph where no trios exist at all	Return -1 after iterating through all possible trios and not finding any.
Large graph with many nodes and edges: potential integer overflow when calculating degree sum.	Use a data type with a larger range (e.g., long) to store the degree sum to prevent integer overflow.
Disconnected graph: some nodes might not belong to any trio	The adjacency matrix or list approach will naturally handle this by not considering nodes in different components together.
Graph represented by adjacency list with unsorted neighbors for each node.	Ensure the algorithm used to find connected trios correctly identifies neighbors regardless of their order in the adjacency list.