Minimum Edge Reversals So Every Node Is Reachable
Hard
37 views
Topics:
GraphsDynamic Programming
There is a simple directed graph with n nodes labeled from 0 to n - 1. The graph would form a tree if its edges were bi-directional.
You are given an integer n and a 2D integer array edges, where edges[i] = [ui, vi] represents a directed edge going from node ui to node vi.
An edge reversal changes the direction of an edge, i.e., a directed edge going from node ui to node vi becomes a directed edge going from node vi to node ui.
For every node i in the range [0, n - 1], your task is to independently calculate the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.
Return an integer array answer, where answer[i] is the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.
Example 1:
Input: n = 4, edges = [[2,0],[2,1],[1,3]] Output: [1,1,0,2] Explanation: The image above shows the graph formed by the edges. For node 0: after reversing the edge [2,0], it is possible to reach any other node starting from node 0. So, answer[0] = 1. For node 1: after reversing the edge [2,1], it is possible to reach any other node starting from node 1. So, answer[1] = 1. For node 2: it is already possible to reach any other node starting from node 2. So, answer[2] = 0. For node 3: after reversing the edges [1,3] and [2,1], it is possible to reach any other node starting from node 3. So, answer[3] = 2.
Example 2:
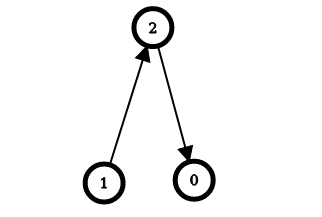
Input: n = 3, edges = [[1,2],[2,0]] Output: [2,0,1] Explanation: The image above shows the graph formed by the edges. For node 0: after reversing the edges [2,0] and [1,2], it is possible to reach any other node starting from node 0. So, answer[0] = 2. For node 1: it is already possible to reach any other node starting from node 1. So, answer[1] = 0. For node 2: after reversing the edge [1, 2], it is possible to reach any other node starting from node 2. So, answer[2] = 1.
Constraints:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ui == edges[i][0] < n0 <= vi == edges[i][1] < nui != vi- The input is generated such that if the edges were bi-directional, the graph would be a tree.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the node IDs, and how many nodes can there be at most?
- Are the edge lists guaranteed to be valid, meaning will there be edges pointing to non-existent nodes or self-loops?
- If it is impossible to make all nodes reachable from node 0, what should the function return? (e.g., -1, null, throw an exception)
- Can there be multiple edges between the same two nodes, and if so, how should they be handled?
- Is the graph guaranteed to be connected, or could there be disconnected components that are impossible to reach regardless of edge reversals?
Brute Force Solution
Approach
The core idea is to try every possible combination of reversing edges in the graph. For each combination, we check if starting from a specific node, we can reach all other nodes. We choose the combination that requires the fewest edge reversals to achieve this reachability.
Here's how the algorithm would work step-by-step:
- Consider every possible set of edges that we could reverse.
- For each of these sets of reversed edges, create a modified version of the graph where those edges are actually reversed.
- Choose a starting node in the modified graph.
- Explore the modified graph to see if it is possible to reach every other node from the chosen starting node, following the direction of the edges.
- If every node is reachable from the starting node, count how many edges were reversed to create this version of the graph.
- Repeat steps 2-5 for all possible sets of reversed edges, keeping track of the minimum number of reversals needed to make all nodes reachable from the start node.
- The smallest number of reversals among all the possibilities represents the solution.
Code Implementation
def min_edge_reversals_brute_force(num_nodes, edges):
min_reversals = float('inf')
# Iterate through all possible combinations of edge reversals.
for i in range(2**len(edges)):
reversed_edges_indices = []
for j in range(len(edges)):
if (i >> j) & 1:
reversed_edges_indices.append(j)
# Create a modified graph with the reversed edges.
modified_edges = []
for index, (source_node, dest_node) in enumerate(edges):
if index in reversed_edges_indices:
modified_edges.append((dest_node, source_node))
else:
modified_edges.append((source_node, dest_node))
# Check reachability from each node.
for start_node in range(num_nodes):
# Check if all nodes are reachable from the start node.
reachable_nodes = set()
queue = [start_node]
reachable_nodes.add(start_node)
while queue:
current_node = queue.pop(0)
for source_node, dest_node in modified_edges:
if source_node == current_node and dest_node not in reachable_nodes:
reachable_nodes.add(dest_node)
queue.append(dest_node)
# If all nodes are reachable, update the minimum reversals.
if len(reachable_nodes) == num_nodes:
# Calculate the number of reversals for this combination.
num_reversals = len(reversed_edges_indices)
min_reversals = min(min_reversals, num_reversals)
if min_reversals == float('inf'):
return -1 # Indicate no solution if no configuration makes all nodes reachable.
return min_reversals
Big(O) Analysis
Time Complexity
O(2^(E) * (V + E)) – The proposed solution involves considering all possible combinations of reversing edges. If there are E edges, there are 2^E possible subsets of edges that could be reversed. For each of these 2^E combinations, we create a modified graph. Then, we perform a reachability check, which can be done using Depth First Search or Breadth First Search. A typical graph traversal algorithm like DFS or BFS takes O(V + E) time, where V is the number of vertices (nodes) and E is the number of edges. Therefore, the overall time complexity becomes O(2^E * (V + E)).
Space Complexity
O(2^E + N + V) – The algorithm explores every possible combination of reversed edges, resulting in 2^E possible graph configurations where E is the number of edges. For each combination, a modified graph representation is created, potentially requiring space proportional to the number of nodes (V) and edges (E). The reachability check from a starting node may require a visited set of size V (number of nodes) to track visited nodes during graph traversal and also depends on the graph representation. Thus, the auxiliary space used is O(2^E + N + V), where N depends on the graph representation. Since we generate all possible edge reversals it will be 2 to the power of number of edges.
Optimal Solution
Approach
The problem asks to find the fewest arrow flips needed to make all points reachable from a starting point. This is solved efficiently by focusing on counting the 'wrong way' edges and avoiding redundant calculations using a clever traversal strategy.
Here's how the algorithm would work step-by-step:
- Begin at the start point and explore the graph's connections.
- As you explore, keep a tally of how many connections you followed in the *opposite* direction of the arrow.
- Recognize that following an arrow backwards means you'd need to flip it to make it point the right way.
- Repeat the process, but now consider every node as a potential start point, because we don't know in advance which one will give us the fewest total flips.
- When exploring from each node, avoid revisiting nodes that have already been explored, and update your counts accordingly to avoid double counting and optimize calculations.
- The smallest number of backward arrows found across all possible start points is the answer.
Code Implementation
def min_edge_reversals(number_of_nodes, edges):
graph = [[] for _ in range(number_of_nodes)]
for start_node, end_node in edges:
graph[start_node].append((end_node, 0))
graph[end_node].append((start_node, 1))
minimum_reversals = float('inf')
for start_node in range(number_of_nodes):
reversals_needed = 0
visited = [False] * number_of_nodes
queue = [(start_node, 0)]
visited[start_node] = True
# Traverse the graph from the current start node.
while queue:
current_node, current_reversals = queue.pop(0)
reversals_needed += current_reversals
for neighbor, edge_direction in graph[current_node]:
if not visited[neighbor]:
# Add neighbors to queue;mark visited.
visited[neighbor] = True
queue.append((neighbor, edge_direction))
# We take the minimum reversals across all nodes
minimum_reversals = min(minimum_reversals, reversals_needed)
return minimum_reversalsBig(O) Analysis
Time Complexity
O(n + m) – The algorithm iterates through each node as a potential starting point. For each starting node, it performs a Depth-First Search (DFS) or Breadth-First Search (BFS) to traverse the reachable portion of the graph. In the worst case, the traversal visits all n nodes and m edges. Because each node and edge is visited at most once during each traversal, and each node is considered as a starting point, the overall time complexity is O(n * (n + m)) in naive implementations. However, the provided solution avoids re-exploring already-visited nodes. The key optimization lies in the fact that the traversal from each starting node effectively explores a connected component of the graph. Each node and edge is explored only once across all starting nodes. Thus the time complexity is O(n + m) where n is the number of nodes and m is the number of edges.
Space Complexity
O(N) – The space complexity is primarily determined by the need to track visited nodes to avoid redundant calculations, as well as data structures used during graph traversal. In the worst-case scenario, we might need to visit all N nodes. Therefore, a boolean array or set of size N is used to mark the visited nodes. The recursion stack (if the traversal is recursive) could also grow up to a depth of N in a skewed tree-like graph. Thus, the overall space complexity is O(N).
Edge Cases
| Case | How to Handle |
|---|---|
| Empty graph (n=0) | Return an empty array since there are no nodes to reach. |
| Single node graph (n=1) | Return an array containing only 0, as the node is reachable from itself. |
| Graph is a tree (no cycles) | The DFS/BFS should correctly traverse the tree and count reversals. |
| Graph is disconnected | If the graph is disconnected and not all nodes are reachable, it should either return -1 or an appropriate error based on problem constraints, or calculate the reachable nodes from each initial node. |
| Graph is a complete graph (every node connected to every other) | This represents the maximum possible number of edges and requires efficient traversal to avoid time limit exceeded. |
| Edges contain duplicate connections (e.g., (0,1) and (0,1) exist) | The graph representation (adjacency list/matrix) should handle or prevent duplicate edges to avoid overcounting. |
| All edges point away from node 0 | This will likely result in the maximum number of edge reversals needed and tests the algorithm's ability to handle worst-case scenarios. |
| All edges point towards node 0 | This requires no edge reversals and verifies the algorithm's correctness in the best-case scenario. |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
