Minimum Fuel Cost to Report to the Capital #18 Most Asked
MediumThere is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of n cities numbered from 0 to n - 1 and exactly n - 1 roads. The capital city is city 0. You are given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi.
There is a meeting for the representatives of each city. The meeting is in the capital city.
There is a car in each city. You are given an integer seats that indicates the number of seats in each car.
A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel.
Return the minimum number of liters of fuel to reach the capital city.
Example 1:

Input: roads = [[0,1],[0,2],[0,3]], seats = 5 Output: 3 Explanation: - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed.
Example 2:
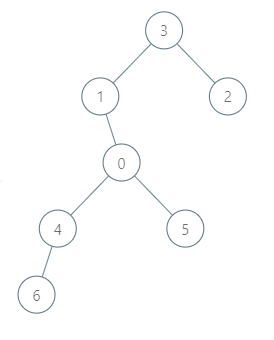
Input: roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2 Output: 7 Explanation: - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed.
Example 3:

Input: roads = [], seats = 1 Output: 0 Explanation: No representatives need to travel to the capital city.
Constraints:
1 <= n <= 105roads.length == n - 1roads[i].length == 20 <= ai, bi < nai != biroadsrepresents a valid tree.1 <= seats <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the number of cities `n` and the `roads` array size? Is there a maximum value?
- Can the input `roads` array be empty, and if so, what should the function return?
- Are the city indices in the `roads` array 0-indexed or 1-indexed?
- Is it guaranteed that the graph formed by the `roads` is connected? If not, how should disconnected components be handled?
- Can the `seats` value be zero or negative? What is the expected behavior if `seats` is 1?
Brute Force Solution
Approach
The goal is to figure out the least amount of fuel needed for everyone to reach the capital city. A brute force approach would explore every single possible travel plan for all individuals, to find the absolute best one.
Here's how the algorithm would work step-by-step:
- Consider every possible path each person could take to the capital.
- For each possible combination of paths (one path per person), calculate the total fuel cost.
- To calculate the fuel cost, determine how many cars are needed on each road segment for that specific combination of paths.
- Sum the number of cars needed across all road segments to get the total fuel cost for that combination.
- Compare the total fuel cost of each path combination with all others.
- The minimum fuel cost among all possible combinations is the answer.
Code Implementation
def minimum_fuel_cost_brute_force(number_of_cities, roads, seats):
def calculate_fuel_cost(paths):
total_fuel_needed = 0
# Iterate through each road to calculate the cars needed
for city_a, city_b in roads:
people_traveling_on_road = 0
for city_index in range(number_of_cities):
path = paths[city_index]
if (city_a in path and city_b in path and path.index(city_a) + 1 == path.index(city_b)) or \
(city_b in path and city_a in path and path.index(city_b) + 1 == path.index(city_a)): # Check if the road is used in the path
people_traveling_on_road += 1
cars_needed = (people_traveling_on_road + seats - 1) // seats
total_fuel_needed += cars_needed
return total_fuel_needed
def find_all_paths_to_capital(start_city, graph, capital_city):
def find_paths(current_city, path):
path = path + [current_city]
if current_city == capital_city:
return [path]
if current_city not in graph:
return []
paths = []
for neighbor in graph[current_city]:
if neighbor not in path:
new_paths = find_paths(neighbor, path)
for new_path in new_paths:
paths.append(new_path)
return paths
return find_paths(start_city, graph, capital_city)
# Build the graph representation of the roads
graph = {i: [] for i in range(number_of_cities)}
for city_a, city_b in roads:
graph[city_a].append(city_b)
graph[city_b].append(city_a)
all_possible_paths = []
for city_index in range(number_of_cities):
all_possible_paths.append(find_all_paths_to_capital(city_index, graph, 0))
# Generate all combinations of paths
import itertools
path_combinations = list(itertools.product(*all_possible_paths))
minimum_fuel = float('inf')
# Need to check every single combo to find the true min
for combination in path_combinations:
fuel_cost = calculate_fuel_cost(combination)
minimum_fuel = min(minimum_fuel, fuel_cost)
return minimum_fuelBig(O) Analysis
Optimal Solution
Approach
The goal is to minimize the fuel needed for everyone to reach the capital. We can achieve this by working backwards from the capital, figuring out how many people travel on each road segment and thus how many cars are needed for that segment.
Here's how the algorithm would work step-by-step:
- Imagine the capital city as the center point and everyone else moving towards it.
- Start at the outer cities and work your way inwards towards the capital.
- For each city, determine how many people (including the initial resident) need to travel through that city to get to the capital.
- Whenever a group of people moves along a road, calculate how many cars are needed to carry them, considering the car capacity.
- The number of cars needed multiplied by the distance (which is always 1 in this problem) gives the fuel cost for that road segment.
- Add up the fuel cost for each road segment to get the total minimum fuel cost for everyone to reach the capital.
Code Implementation
def minimum_fuel_cost(number_of_cities, roads, seats):
adjacency_list = [[] for _ in range(number_of_cities)]
for city_one, city_two in roads:
adjacency_list[city_one].append(city_two)
adjacency_list[city_two].append(city_one)
fuel_needed = 0
people_in_city = [1] * number_of_cities
visited = [False] * number_of_cities
def dfs(current_city):
nonlocal fuel_needed
visited[current_city] = True
for neighbor_city in adjacency_list[current_city]:
if not visited[neighbor_city]:
dfs(neighbor_city)
# Count people travelling on each road segment
people_in_city[current_city] += people_in_city[neighbor_city]
# Determine the number of cars needed on each road
cars_needed = (people_in_city[neighbor_city] + seats - 1) // seats
# Calculate the fuel needed for each road and accumulate it
if current_city != 0:
fuel_needed += cars_needed
dfs(0)
return fuel_neededBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty roads array | Return 0 as no travel is required when there are no roads. |
| n = 1 (single city) | Return 0 as there's only the capital and no travel cost. |
| seats = 1 (each person needs a car) | The total number of people across all cities except the capital is the fuel cost. |
| seats = infinity (all people fit in one car) | This is equivalent to only needing one car per level away from the capital, so cost is the number of non-capital cities. |
| Star graph (one city connected to all others) | The solution should efficiently sum up the car trips for each city connected to the capital. |
| Line graph (cities connected in a line) | Ensure the recursive/DFS calculation traverses the line correctly from the leaf nodes. |
| Integer overflow of fuel cost (very large n or skewed population) | Use long long to accumulate the fuel cost to prevent overflow issues. |
| Disconnection graph (some cities not connected to the capital) | The algorithm should only consider connected components and not get stuck in an infinite loop or incorrect calculation by design from the problem statement where all cities are assumed to be connected. |