Minimum Number of Food Buckets to Feed the Hamsters

Medium

Grab

5 views

Topics:

ArraysGreedy Algorithms

You are given a 0-indexed string hamsters where hamsters[i] is either:

'H' indicating that there is a hamster at index i, or
'.' indicating that index i is empty.

You will add some number of food buckets at the empty indices in order to feed the hamsters. A hamster can be fed if there is at least one food bucket to its left or to its right. More formally, a hamster at index i can be fed if you place a food bucket at index i - 1 and/or at index i + 1.

Return the minimum number of food buckets you should place at empty indices to feed all the hamsters or -1 if it is impossible to feed all of them.

Example 1:

Input: hamsters = "H..H"
Output: 2
Explanation: We place two food buckets at indices 1 and 2.
It can be shown that if we place only one food bucket, one of the hamsters will not be fed.

Example 2:

Input: hamsters = ".H.H."
Output: 1
Explanation: We place one food bucket at index 2.

Example 3:

Input: hamsters = ".HHH."
Output: -1
Explanation: If we place a food bucket at every empty index as shown, the hamster at index 2 will not be able to eat.

Constraints:

1 <= hamsters.length <= 10⁵
hamsters[i] is either'H' or '.'.

Try coding it in LeetCode

Minimum Number of Food Buckets to Feed the Hamsters

Medium

Grab

5 views

Topics:

ArraysGreedy Algorithms

You are given a 0-indexed string hamsters where hamsters[i] is either:

'H' indicating that there is a hamster at index i, or
'.' indicating that index i is empty.

You will add some number of food buckets at the empty indices in order to feed the hamsters. A hamster can be fed if there is at least one food bucket to its left or to its right. More formally, a hamster at index i can be fed if you place a food bucket at index i - 1 and/or at index i + 1.

Return the minimum number of food buckets you should place at empty indices to feed all the hamsters or -1 if it is impossible to feed all of them.

Example 1:

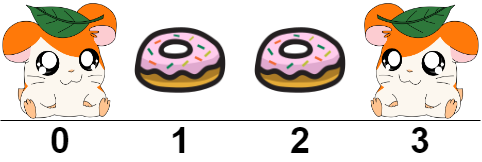
Input: hamsters = "H..H"
Output: 2
Explanation: We place two food buckets at indices 1 and 2.
It can be shown that if we place only one food bucket, one of the hamsters will not be fed.

Example 2:

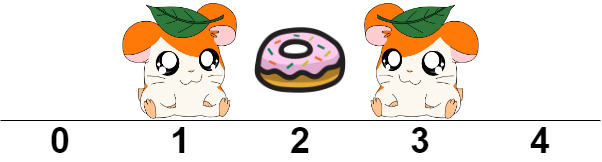
Input: hamsters = ".H.H."
Output: 1
Explanation: We place one food bucket at index 2.

Example 3:

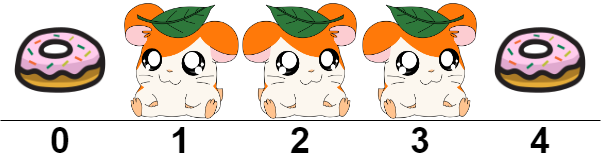
Input: hamsters = ".HHH."
Output: -1
Explanation: If we place a food bucket at every empty index as shown, the hamster at index 2 will not be able to eat.

Constraints:

1 <= hamsters.length <= 10⁵
hamsters[i] is either'H' or '.'.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Can the input string `hamsters` be empty or null?
What are the possible characters in the input string other than 'H' and '.'? Should I assume only these two?
If it's impossible to feed all hamsters, what should I return?
Is it possible to have consecutive 'H' characters in the input string?
Should I optimize for any particular time or space complexity given potentially large input strings?

Brute Force Solution

Approach

The goal is to figure out the fewest food buckets needed to feed hamsters lined up in a row, where we can only place buckets next to hamsters and not next to each other. The brute force approach here means trying every possible arrangement of buckets and counting how many we used.

Here's how the algorithm would work step-by-step:

Consider all the possible places where you could put a food bucket.
Start by placing a bucket in the very first available spot.
Then, check if this bucket covers all the hamsters that need food. If it does, you're done, and you only needed one bucket!
If not, try adding another bucket in the next available spot. Keep checking if all hamsters are fed after adding each bucket.
Continue this process, adding buckets one by one in every possible location combination until you find an arrangement that feeds all the hamsters.
Each time you find a complete and valid arrangement, remember how many buckets you used.
After trying every possible combination of bucket placements, choose the arrangement that used the fewest buckets.

Code Implementation

def minimum_buckets_brute_force(hamster_string):
    minimum_number_of_buckets = float('inf')
    number_of_positions = len(hamster_string)

    def solve(index, current_buckets):
        nonlocal minimum_number_of_buckets

        if index == number_of_positions:
            if is_valid_arrangement(hamster_string, current_buckets):
                minimum_number_of_buckets = min(minimum_number_of_buckets, sum(current_buckets))
            return

        # Try placing a bucket at the current index
        current_buckets[index] = 1
        solve(index + 1, current_buckets)

        # Try not placing a bucket at the current index
        current_buckets[index] = 0
        solve(index + 1, current_buckets)

    def is_valid_arrangement(hamster_string, current_buckets):
        # Check if every hamster is fed
        for hamster_index in range(len(hamster_string)):
            if hamster_string[hamster_index] == 'H':
                is_fed = False
                # Check left neighbor
                if hamster_index > 0 and current_buckets[hamster_index - 1] == 1:
                    is_fed = True
                # Check right neighbor
                if hamster_index < len(hamster_string) - 1 and current_buckets[hamster_index + 1] == 1:
                    is_fed = True
                if not is_fed:
                    return False
        return True

    current_buckets = [0] * number_of_positions

    # Start the recursive process to find the minimum
    solve(0, current_buckets)

    if minimum_number_of_buckets == float('inf'):
        return -1
    else:
        return minimum_number_of_buckets

Big(O) Analysis

Time Complexity

O(2^n) – The described brute force approach involves considering all possible arrangements of buckets. Since each position can either have a bucket or not, there are 2 options for each of the n positions in the row. This results in 2^n possible combinations to check. The time complexity arises from exhaustively examining all these combinations to find the minimum number of buckets needed. Therefore, the time complexity is O(2^n).

Space Complexity

O(2^N) – The described brute force approach involves trying every possible arrangement of buckets. In the worst-case scenario, we explore all subsets of positions to place buckets. Representing each possible arrangement requires storing a combination of bucket placements. Since there are potentially 2^N possible subsets of positions where N is the length of the input string, the space needed to store and explore these arrangements grows exponentially. Therefore, the auxiliary space complexity is O(2^N).

Optimal Solution

Approach

The core idea is to strategically place buckets to cover hamsters while avoiding placing buckets directly next to each other. We scan the row from left to right, making local decisions that ultimately minimize the total number of buckets needed.

Here's how the algorithm would work step-by-step:

Start at the beginning of the row of positions.
If a position has a hamster and neither of its neighbors have buckets, try to place a bucket next to it.
Prioritize placing the bucket to the right of the hamster if possible, as that avoids interfering with bucket placements to the left.
If placing to the right isn't possible (e.g., end of the row or another hamster is there), place the bucket to the left if it's available.
If a hamster position cannot have a bucket placed next to it (e.g., buckets are already on both sides or there is no room), it means we can't feed that hamster, so we return -1 (meaning impossible).
Keep track of the number of buckets you've placed.
Move to the next position and repeat until you've covered the entire row.
Return the total count of buckets used.

Code Implementation

def minimum_buckets(hamsters_string):
    number_of_hamsters = len(hamsters_string)
    hamsters_array = list(hamsters_string)
    food_buckets_count = 0

    for i in range(number_of_hamsters):
        if hamsters_array[i] == 'H':
            #Check left neighbor first.
            if i > 0 and hamsters_array[i - 1] == 'B':
                continue

            #Check right neighbor.
            if i < number_of_hamsters - 1 and hamsters_array[i + 1] == 'B':
                continue

            #Place bucket to the right if possible.
            if i < number_of_hamsters - 1:
                hamsters_array[i + 1] = 'B'
                food_buckets_count += 1
            #If can't place right, place to the left.
            elif i > 0:
                hamsters_array[i - 1] = 'B'
                food_buckets_count += 1
            else:
                #No neighbors to place food.
                return -1

    return food_buckets_count

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through the input string `street` of length n exactly once. During each iteration, it performs a constant number of checks to determine bucket placement (checking neighbors and updating the count). Since the number of operations within the loop does not depend on the size of the input, the overall time complexity is directly proportional to the length of the string, resulting in O(n).

Space Complexity

O(1) – The algorithm uses a constant amount of extra space. It only keeps track of the number of buckets placed, which is stored in a single variable. No additional data structures, such as lists or hash maps, are used that scale with the input size N (the length of the row). Therefore, the space complexity is independent of the input size and remains constant.

Edge Cases

Case	How to Handle
Null or empty input string	Return 0 immediately since there are no hamsters to feed.
String of length 1 ('H' or '.')	If 'H', return -1 because a single hamster cannot be fed; if '.', return 0.
String contains only hamsters ('HHHHH')	Return -1, since no hamster can be fed without an empty space.
String contains only empty cells ('.....')	Return 0 because there are no hamsters to feed.
Alternating hamsters and empty cells ('H.H.H')	Requires buckets in every empty cell, so count and return them.
Two adjacent hamsters with empty cells on either side (' .HH. ')	Requires only one bucket to feed both hamsters; optimize bucket placement to minimize the count.
Hamster at the beginning or end of the string ('H....' or '....H')	Bucket must be placed to the right or left of the hamster, respectively, if possible.
String with consecutive hamsters at the beginning or end	If empty spaces exist, handle them according to above rules; otherwise return -1 if no empty spots exist.