Minimum Number of Operations to Sort a Binary Tree by Level
Minimum Number of Operations to Sort a Binary Tree by Level #3 Most Asked
MediumYou are given the root of a binary tree with unique values.
In one operation, you can choose any two nodes at the same level and swap their values.
Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.
The level of a node is the number of edges along the path between it and the root node.
Example 1:
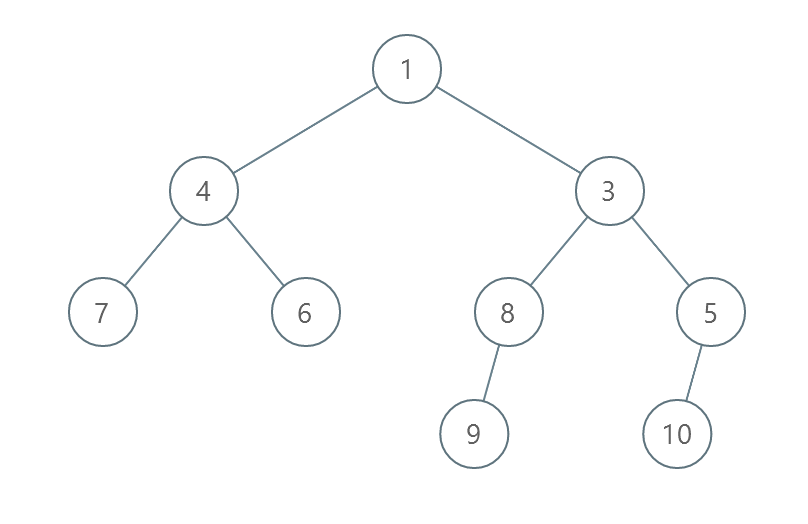
Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10] Output: 3 Explanation: - Swap 4 and 3. The 2nd level becomes [3,4]. - Swap 7 and 5. The 3rd level becomes [5,6,8,7]. - Swap 8 and 7. The 3rd level becomes [5,6,7,8]. We used 3 operations so return 3. It can be proven that 3 is the minimum number of operations needed.
Example 2:
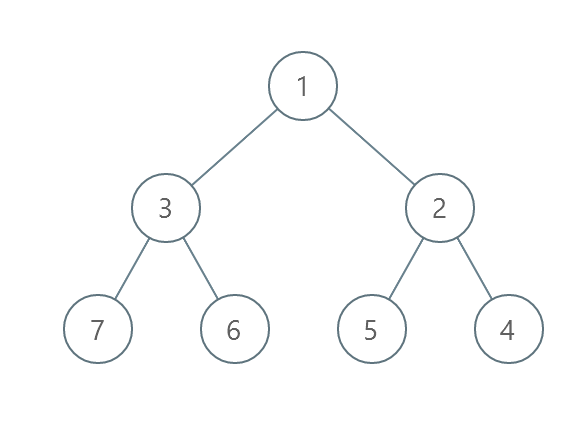
Input: root = [1,3,2,7,6,5,4] Output: 3 Explanation: - Swap 3 and 2. The 2nd level becomes [2,3]. - Swap 7 and 4. The 3rd level becomes [4,6,5,7]. - Swap 6 and 5. The 3rd level becomes [4,5,6,7]. We used 3 operations so return 3. It can be proven that 3 is the minimum number of operations needed.
Example 3:

Input: root = [1,2,3,4,5,6] Output: 0 Explanation: Each level is already sorted in increasing order so return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 105- All the values of the tree are unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that the nodes in the binary tree can have? Are they guaranteed to be positive integers?
- What should I return if the root of the binary tree is null or empty?
- When you say 'sorted by level', are you asking for the nodes at each level to be sorted in ascending order from left to right?
- If multiple sequences of swaps achieve the minimum number of operations, is any one of them acceptable?
- How deep can the tree be (maximum number of levels), and how many nodes can be on a single level, in the worst-case scenario?
Brute Force Solution
Approach
The brute force approach for sorting a binary tree level by level is like trying every single possible arrangement of the numbers on each level. We'll check if that arrangement gets us closer to a sorted order and then count the swaps to get there, repeating this for all levels.
Here's how the algorithm would work step-by-step:
- Look at the very first level of the tree (the root).
- Find all possible orderings of the values at that level. Think of it like shuffling a deck of cards to find every arrangement.
- For each arrangement, count how many swaps it would take to sort the values at that level.
- Move down to the next level of the tree.
- Again, find all possible orderings for the values at this level and count the swaps for each.
- Continue this process level by level, keeping track of the minimum number of swaps needed for each level.
- Add up the minimum number of swaps from all levels to get the overall minimum swaps needed to sort the entire tree level by level. This is your final answer after having checked all possibilities.
Code Implementation
from collections import deque
def minimum_swaps_to_sort_binary_tree_level_by_level(root):
if not root:
return 0
total_swaps = 0
queue = deque([root])
while queue:
level_size = len(queue)
level_values = []
for _ in range(level_size):
node = queue.popleft()
level_values.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# Convert values to indices for permutation
indices = list(range(len(level_values)))
min_swaps_for_level = float('inf')
import itertools
# Iterate through all possible permutations
for permutation in itertools.permutations(indices):
swaps = 0
temp_level_values = level_values[:] # Create a copy
# Apply the permutation to the level values
for i, index in enumerate(permutation):
temp_level_values[i] = level_values[index]
# Calculate swaps to sort the permuted list
swaps = calculate_minimum_swaps_to_sort(temp_level_values)
min_swaps_for_level = min(min_swaps_for_level, swaps)
total_swaps += min_swaps_for_level
return total_swaps
def calculate_minimum_swaps_to_sort(array):
array_length = len(array)
index_map = {value: index for index, value in enumerate(array)}
swaps = 0
visited = [False] * array_length
for i in range(array_length):
if visited[i] or index_map[array[i]] == i:
continue
cycle_size = 0
j = i
# Traverse the cycle
while not visited[j]:
visited[j] = True
j = index_map[array[j]]
cycle_size += 1
# Swaps needed equals cycle size - 1
if cycle_size > 0:
swaps += (cycle_size - 1)
return swaps
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = rightBig(O) Analysis
Optimal Solution
Approach
The goal is to sort each level of the tree with the fewest swaps. We process each level separately and use a clever trick to count how many swaps are needed to put the numbers in order without actually performing the swaps.
Here's how the algorithm would work step-by-step:
- Go through the tree level by level.
- For each level, create a list of the values currently present in that level.
- Determine the sorted order of values for that level without changing the original list. This provides the target arrangement.
- Now, count the number of swaps needed to transform the original list into the sorted list *without* actually doing the swaps. We do this by recognizing cycles.
- A cycle represents a group of misplaced elements that need to be rearranged as a group to reach their sorted positions.
- The number of swaps needed for a cycle is always one less than the number of elements in that cycle.
- Sum the swap counts for all cycles within the level to get the total swaps needed for that level.
- Add up the total swap counts for all levels to get the overall minimum swap count needed to sort the entire tree by levels.
Code Implementation
from collections import deque
def minimum_operations_to_sort_a_binary_tree_by_level(root):
if not root:
return 0
total_swaps = 0
queue = deque([root])
while queue:
level_size = len(queue)
current_level_values = []
for _ in range(level_size):
node = queue.popleft()
current_level_values.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# Get the indices that would sort the array.
sorted_indices = sorted(range(len(current_level_values)), key=lambda k: current_level_values[k])
visited = [False] * len(current_level_values)
level_swaps = 0
# Cycle detection and swap counting.
for i in range(len(current_level_values)):
if visited[i] or sorted_indices[i] == i:
continue
cycle_size = 0
j = i
# Traverse the cycle to determine the size
while not visited[j]:
visited[j] = True
j = sorted_indices[j]
cycle_size += 1
# Swaps needed is cycle size - 1.
level_swaps += cycle_size - 1
# Accumulate swaps needed for the current level.
total_swaps += level_swaps
return total_swapsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node (empty tree) | Return 0 immediately as there are no levels to sort, avoiding null pointer exceptions. |
| Single-node tree | Return 0 as a single node level is already sorted, minimizing unnecessary processing. |
| Complete binary tree with a large number of nodes | Ensure the BFS traversal and sorting algorithm scales efficiently in terms of memory and time complexity to avoid timeouts. |
| Binary tree where all nodes in a level have the same value | The sorting algorithm should correctly handle duplicate values, potentially resulting in 0 swaps for that level. |
| Skewed binary tree (e.g., all nodes on the left) | BFS should handle this case gracefully without excessive memory consumption or stack overflow issues from imbalanced tree height. |
| Binary tree with Integer.MAX_VALUE or Integer.MIN_VALUE values in nodes | The sorting algorithm should correctly compare these extreme values without causing integer overflow during comparisons or calculations. |
| Binary tree where a level is already sorted | The solution correctly calculates the minimum swaps required, which would be 0 if the level is pre-sorted, thus optimizing unnecessary sorting. |
| Deeply unbalanced tree causing excessive queue size in BFS | Consider using iterative deepening depth-first search (IDDFS) as an alternative to BFS if memory usage becomes a bottleneck. |