Minimum Number of Vertices to Reach All Nodes
MediumGiven a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.
Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
Example 1:
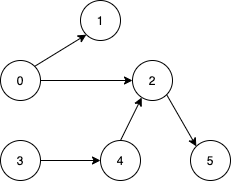
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]] Output: [0,3] Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].
Example 2:
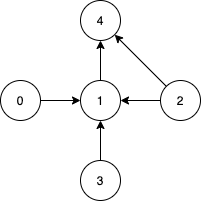
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]] Output: [0,2,3] Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
Constraints:
2 <= n <= 10^51 <= edges.length <= min(10^5, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi < n- All pairs
(fromi, toi)are distinct.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range for the number of nodes `n`? Can I assume it fits within a 32-bit integer?
- Are the edges in the `edges` list directed or undirected?
- Is it guaranteed that the graph is a directed acyclic graph (DAG)?
- If there are multiple sets of vertices that cover all nodes, is any valid set acceptable, or is there a specific criteria to choose one (e.g., the set with the fewest vertices)?
- Can the `edges` list be empty? If so, what should I return?
Brute Force Solution
Approach
The brute force approach for this problem is like trying out every single combination of starting points and seeing if we can reach all locations. We explore every possibility, even if it takes a long time, to guarantee we find the right set of starting points.
Here's how the algorithm would work step-by-step:
- First, consider each location as a potential starting point, one at a time.
- For each potential starting point, trace all the paths that can be reached from it.
- See if starting from just that single location allows you to reach every other location.
- If that doesn't work, try combining pairs of starting locations.
- Check if starting from that pair of locations allows you to reach every other location.
- Keep going, testing combinations of three, four, five, and so on, until you've tried all possible combinations of starting locations.
- As you try different combinations, keep track of the smallest set of starting points that can reach every location.
- Finally, report this smallest set of starting points.
Code Implementation
def minimum_vertices_to_reach_all_nodes_brute_force(number_of_nodes, edges):
all_nodes = set(range(number_of_nodes))
minimum_size_subset = list(range(number_of_nodes))
for subset_size in range(1, number_of_nodes + 1):
import itertools
for combination in itertools.combinations(range(number_of_nodes), subset_size):
reachable_nodes = set()
starting_nodes = list(combination)
# Explore all reachable nodes from the selected subset.
for start_node in starting_nodes:
nodes_to_visit = [start_node]
visited_nodes = {start_node}
while nodes_to_visit:
current_node = nodes_to_visit.pop(0)
reachable_nodes.add(current_node)
for start_node_edge, end_node_edge in edges:
if start_node_edge == current_node:
if end_node_edge not in visited_nodes:
nodes_to_visit.append(end_node_edge)
visited_nodes.add(end_node_edge)
# Check if all nodes are reachable from this subset
if reachable_nodes == all_nodes:
if subset_size < len(minimum_size_subset):
minimum_size_subset = list(combination)
return sorted(minimum_size_subset)
# This function will determine the potential starting points
# from which we can reach all other nodes.
# First, we try single element subsets, then pairs and so on.Big(O) Analysis
Optimal Solution
Approach
The problem asks for the fewest starting points needed to visit every location in a network. The key insight is to identify locations that are only reachable from other locations, meaning nothing points to them. These 'entry point' locations must be our starting points.
Here's how the algorithm would work step-by-step:
- Think of the network as a map where some locations have routes leading into them and out of them.
- Identify locations that have routes leading into them. These locations are reachable from somewhere else.
- Now, find the locations that *do not* have any routes leading into them. These are locations you can only get to if you start there.
- These locations without incoming routes are your required starting points. You need to start at each of these to be able to reach every location on the map.
- The set of these starting point locations is the smallest set of locations needed to reach every location in the network.
Code Implementation
def find_smallest_set_of_vertices(number_of_nodes, edges):
incoming_edges = [False] * number_of_nodes
# Mark nodes with incoming edges
for edge_start, edge_end in edges:
incoming_edges[edge_end] = True
minimum_set = []
# Add nodes without incoming edges to result
# These are the entry points to the graph.
for node_index in range(number_of_nodes):
if not incoming_edges[node_index]:
minimum_set.append(node_index)
return minimum_setBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty graph (n=0) | Return an empty list, as there are no vertices to select. |
| Graph with a single node and no edges | Return a list containing only the single node (index 0). |
| Graph where all nodes are reachable from a single source node | The solution should return only the source node's index. |
| Graph with a cycle; all nodes are mutually reachable | The solution should return nodes with in-degree 0 (if any), as those are the entry points. |
| Maximum number of nodes and edges (scalability) | Ensure the chosen algorithm (e.g., based on in-degree calculation) performs efficiently with large graphs, potentially using appropriate data structures to avoid O(n^2) complexity. |
| Disconnected graph; multiple components requiring multiple source nodes | The solution correctly identifies and returns all nodes with in-degree 0, representing the entry points of each disconnected component. |
| Graph represented with self-loops (an edge from a node to itself) | Self-loops do not affect the in-degree of other nodes and do not need special treatment, as the algorithm only cares about incoming edges from *other* nodes. |
| Graph where a node has edges to all other nodes | This node won't be in the result, and the other nodes' in-degrees will be updated appropriately. |