Minimum Time to Collect All Apples in a Tree

Medium

Cisco

3 views

Topics:

TreesGraphsRecursion

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [a_i, b_i] means that exists an edge connecting the vertices a_i and b_i. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

Example 1:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 2:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

1 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= a_i < b_i <= n - 1
hasApple.length == n

Try coding it in LeetCode

Minimum Time to Collect All Apples in a Tree

Medium

Cisco

3 views

Topics:

TreesGraphsRecursion

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [a_i, b_i] means that exists an edge connecting the vertices a_i and b_i. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

Example 1:

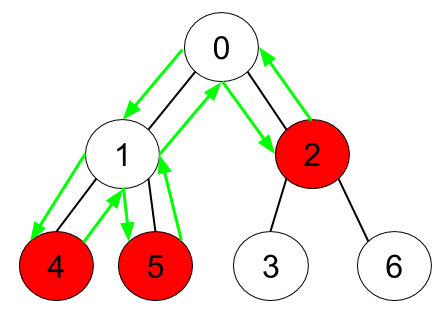
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 2:

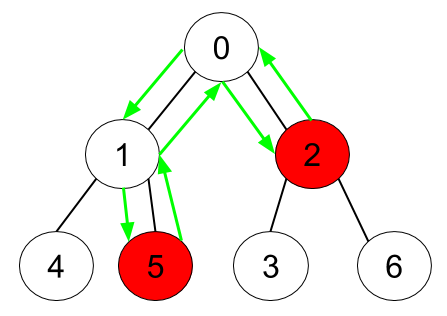
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

1 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= a_i < b_i <= n - 1
hasApple.length == n

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range for the number of nodes 'n' in the tree? Is it safe to assume 'n' will always be a reasonable size, or should I be concerned about potential stack overflow with a recursive solution?
Can the 'edges' list contain duplicate edges or edges that connect a node to itself?
If no apples are present in the tree, should I return 0, or is there another specific value I should return to indicate an empty tree with no apples?
Is it guaranteed that the input graph will always be a valid tree (connected and acyclic)?
Are the 'apples' boolean list indices aligned with the node numbers? For example, does apples[0] indicate whether node 0 has an apple?

Brute Force Solution

Approach

The brute force approach to collecting apples involves exploring every possible path through the tree. We will try every single way to travel the tree's connections, checking if we reach apples. We'll keep track of the total time each path takes and eventually select the shortest one.

Here's how the algorithm would work step-by-step:

Start at the root of the tree.
Imagine taking every possible path from the root. For each connection, try going one way, then try going the other way (if there is another way).
As you travel along each path, check if you find an apple at each location.
If you find an apple, remember that you've found it.
Keep track of how much time each path takes to travel.
If a path leads you to a place you have already visited, you don't need to explore it again from there, and you should return back to the previous place.
Once you've explored all possible paths and collected all the apples, find the path that took the least amount of time to collect all the apples.
That shortest time is your answer.

Code Implementation

def min_time_to_collect_apples_brute_force(number_of_nodes, edges, has_apple):
    graph = [[] for _ in range(number_of_nodes)]
    for start_node, end_node in edges:
        graph[start_node].append(end_node)
        graph[end_node].append(start_node)

    minimum_time = float('inf')

    def depth_first_search(current_node, visited_nodes, collected_apples, current_time):
        nonlocal minimum_time

        #Avoid infinite loops by not revisiting nodes.
        if current_node in visited_nodes:
            return

        visited_nodes.add(current_node)

        if has_apple[current_node]:
            collected_apples.add(current_node)

        if len(collected_apples) == sum(has_apple): 
            minimum_time = min(minimum_time, current_time)
            return

        for neighbor in graph[current_node]:
            depth_first_search(neighbor, visited_nodes.copy(), collected_apples.copy(), current_time + 2)

    # Start the search from the root node (node 0).
    depth_first_search(0, set(), set(), 0)

    if minimum_time == float('inf'):
        return 0
    else:
        return minimum_time

Big(O) Analysis

Time Complexity

O(n!) – The described brute-force approach explores every possible path in the tree. In the worst-case scenario, the algorithm essentially tries all permutations of visiting the nodes. With n nodes, the number of possible paths to explore grows factorially. Therefore, the algorithm's runtime is dominated by the need to explore all permutations. This results in approximately n! operations, thus the time complexity is O(n!).

Space Complexity

O(N) – The brute force approach uses recursion to explore every possible path. In the worst-case scenario, the recursion depth could be proportional to the number of nodes in the tree, N. Additionally, the algorithm keeps track of visited locations to avoid revisiting nodes, which could use a set or array of size N. Therefore, the auxiliary space used by the algorithm is O(N) due to the recursion stack and the visited set.

Optimal Solution

Approach

The most efficient way to solve this problem is to explore the tree from the 'root' down, but only go where we need to. We only care about branches that lead to apples, so we can ignore unnecessary paths.

Here's how the algorithm would work step-by-step:

Start at the beginning (the root of the tree).
Look at each connection leading away from where you are.
If a connection leads to a location with an apple, or a location that eventually leads to an apple, count the trip there and back.
If a connection leads to a location that doesn't have an apple and doesn't lead to any apples further down the path, ignore that connection completely.
Continue this process for all relevant locations, only counting trips on paths that are actually needed to collect apples.
The total count of all trips represents the minimum time required to collect all apples.

Code Implementation

def minTimeToCollectAllApples(number_of_nodes: int, edges: list[list[int]], hasApple: list[bool]) -> int:

    graph = [[] for _ in range(number_of_nodes)]
    for start_node, end_node in edges:
        graph[start_node].append(end_node)
        graph[end_node].append(start_node)

    def depthFirstSearch(current_node: int, parent_node: int) -> int:
        total_time = 0

        # Iterate through all adjacent nodes.
        for neighbor_node in graph[current_node]:
            if neighbor_node != parent_node:
                neighbor_time = depthFirstSearch(neighbor_node, current_node)

                # Add to the total time if subtree has apples
                if neighbor_time > 0 or hasApple[neighbor_node]:
                    total_time += neighbor_time + 2

        return total_time

    # Start traversal from the root node (node 0).
    # Accumulate time only for necessary branches
    return depthFirstSearch(0, -1)

Big(O) Analysis

Time Complexity

O(n) – The provided solution performs a Depth-First Search (DFS) or Breadth-First Search (BFS) traversal of the tree. In the worst-case scenario, we might need to visit all n nodes of the tree to determine which branches lead to apples. The algorithm avoids exploring unnecessary branches that don't lead to apples, but each edge is examined at most twice (once in each direction). Thus, the time complexity is directly proportional to the number of nodes (or edges, since a tree with n nodes has n-1 edges), resulting in O(n).

Space Complexity

O(N) – The algorithm implicitly utilizes a recursion stack to explore the tree. In the worst-case scenario, the tree might resemble a linked list, resulting in recursive calls that go as deep as N, where N is the number of nodes in the tree. Each recursive call adds a new frame to the stack, leading to O(N) space usage for the call stack. Therefore, the auxiliary space complexity is O(N).

Edge Cases

Case	How to Handle
Null or empty edges list	Return 0 immediately, as there are no paths to traverse.
Null or empty hasApple list	Treat all nodes as not having apples; the algorithm should still function correctly and potentially return 0.
Single node graph (edges is empty) with an apple	Return 0, as there is no path to traverse, and we start at node 0.
Single node graph (edges is empty) without an apple	Return 0, as there is no path to traverse, and we start at node 0.
Graph with no apples	Return 0, as no edges need to be traversed to collect apples.
Disconnected graph (not all nodes are reachable from node 0)	Only the connected component containing node 0 is relevant; unreachable nodes don't contribute to the apple collection time.
Graph with a cycle	The algorithm must avoid infinite loops by tracking visited nodes during the depth-first search or breadth-first search traversal.
Maximum number of nodes (e.g., 10^5) and deeply nested tree structure, potentially leading to stack overflow with recursion	Consider using iterative depth-first search (DFS) with a stack to avoid recursion depth limits.