Minimum Time to Type Word Using Special Typewriter

#2 Most AskedEasy

Minimum Time to Type Word Using Special Typewriter #2 Most Asked

Easy

22 views

Topics:

StringsGreedy Algorithms

There is a special typewriter with lowercase English letters 'a' to 'z' arranged in a circle with a pointer. A character can only be typed if the pointer is pointing to that character. The pointer is initially pointing to the character 'a'.

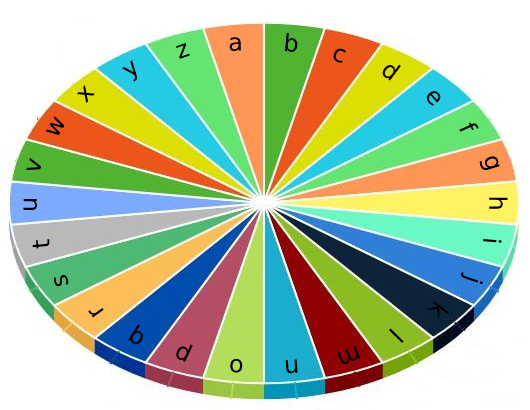
Each second, you may perform one of the following operations:

Move the pointer one character counterclockwise or clockwise.
Type the character the pointer is currently on.

Given a string word, return the minimum number of seconds to type out the characters in word.

Example 1:

Input: word = "abc"
Output: 5
Explanation: 
The characters are printed as follows:
- Type the character 'a' in 1 second since the pointer is initially on 'a'.
- Move the pointer clockwise to 'b' in 1 second.
- Type the character 'b' in 1 second.
- Move the pointer clockwise to 'c' in 1 second.
- Type the character 'c' in 1 second.

Example 2:

Input: word = "bza"
Output: 7
Explanation:
The characters are printed as follows:
- Move the pointer clockwise to 'b' in 1 second.
- Type the character 'b' in 1 second.
- Move the pointer counterclockwise to 'z' in 2 seconds.
- Type the character 'z' in 1 second.
- Move the pointer clockwise to 'a' in 1 second.
- Type the character 'a' in 1 second.

Example 3:

Input: word = "zjpc"
Output: 34
Explanation:
The characters are printed as follows:
- Move the pointer counterclockwise to 'z' in 1 second.
- Type the character 'z' in 1 second.
- Move the pointer clockwise to 'j' in 10 seconds.
- Type the character 'j' in 1 second.
- Move the pointer clockwise to 'p' in 6 seconds.
- Type the character 'p' in 1 second.
- Move the pointer counterclockwise to 'c' in 13 seconds.
- Type the character 'c' in 1 second.

Constraints:

1 <= word.length <= 100
word consists of lowercase English letters.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Is the `word` guaranteed to contain only lowercase English letters, or can it contain other characters?
Can the `word` be empty or null?
If the typewriter starts at 'a', is the distance to a letter calculated clockwise or counter-clockwise, or is the minimum of both considered?
Is there a limit on the length of the `word`?
Does pressing the button to type a letter always take one unit of time, regardless of the distance moved on the typewriter?

Brute Force Solution

Approach

The basic idea is to try every possible sequence of rotations and keystrokes to type the word. We'll simulate the typing process, exploring all possible paths the typewriter head can take, and record the time taken for each path.

Here's how the algorithm would work step-by-step:

Start with the typewriter head at the first letter (A).
Consider every letter in the word we need to type, one at a time.
For each letter, figure out if it's faster to move the head clockwise or counter-clockwise to that letter.
Calculate the number of steps (rotations) it takes to reach that letter in each direction and the single keystroke to type that letter.
Add the minimum number of rotations (either clockwise or counter-clockwise) and one keystroke to the total time.
Repeat this process for every letter in the word, always starting from the previous letter's position.
The final total time will be the brute force solution.

Code Implementation

def min_time_to_type_brute_force(word):
    current_letter = 'a'
    total_time = 0

    for target_letter in word:
        # Find the distance clockwise
        clockwise_distance = (ord(target_letter) - ord(current_letter)) % 26

        # Find the distance counter-clockwise
        counterclockwise_distance = (ord(current_letter) - ord(target_letter)) % 26

        # Choose the minimum distance to move the typewriter head
        total_time += min(clockwise_distance, counterclockwise_distance)

        # Add the time for the keystroke
        total_time += 1

        # Update the current letter to the target letter
        current_letter = target_letter

    return total_time

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through each character of the input word of length n. For each character, it calculates the distance to the next character on the typewriter. The distance calculation takes constant time, as it involves determining the shorter of the clockwise and counter-clockwise rotations, which are fixed calculations. Therefore, the time complexity is directly proportional to the length of the word, resulting in O(n).

Space Complexity

O(1) – The described brute force solution calculates the minimum time iteratively without using any auxiliary data structures that scale with the input size. It only uses a constant amount of extra space for variables like the current character position and the total time. Therefore, the space complexity is constant, independent of the length of the word (N).

Optimal Solution

Approach

The goal is to find the fewest moves to type a word on a special typewriter. The typewriter only moves clockwise and you need to press a button to type each character. The clever idea is to always choose the shortest rotational distance between the current letter and the target letter.

Here's how the algorithm would work step-by-step:

Begin with the typewriter cursor at the letter 'a'.
For each letter in the target word, calculate the clockwise and counter-clockwise distance from the current typewriter letter to the target letter.
Choose the shorter of the two distances. This will be the number of rotational moves you make.
Add one move for the key press to type the letter.
Move the typewriter cursor to the typed letter.
Repeat steps 2-5 for all letters in the target word.
Sum up all the moves (rotations + key presses) to get the minimum time to type the word.

Code Implementation

def minTimeToType(word):
    current_letter = 'a'
    total_moves = 0

    for target_letter in word:
        # Calculate the clockwise distance
        clockwise_distance = abs(ord(target_letter) - ord(current_letter))

        # Calculate counter-clockwise distance
        counterclockwise_distance = 26 - clockwise_distance

        # Choose the minimum distance
        rotational_moves = min(clockwise_distance, counterclockwise_distance)
        total_moves += rotational_moves

        # Add one move for the key press
        total_moves += 1

        current_letter = target_letter

    return total_moves

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through each character of the input word once. For each character, it calculates the distance to the current character on the typewriter. This distance calculation involves a constant number of operations. Since the number of operations within the loop is constant and the loop runs n times (where n is the length of the word), the overall time complexity is O(n).

Space Complexity

O(1) – The algorithm uses a fixed number of variables to store the current letter and the target letter, along with variables to keep track of the distances and the total moves. The space used by these variables does not depend on the length of the input word. Therefore, the auxiliary space complexity is constant.

Edge Cases

Case	How to Handle
Null or empty word	Return 0 as no time is needed to type an empty word.
Word with only one character	Return the absolute difference between the starting position 'a' and the single character.
Word with all identical characters	The solution correctly calculates the time based on the repetitive character.
Word with characters in increasing alphabetical order (e.g., 'abc')	The solution should efficiently calculate the sum of consecutive differences, which are all 1.
Word with characters in decreasing alphabetical order (e.g., 'cba')	The solution correctly calculates the sum of consecutive differences.
Word with characters oscillating back and forth (e.g., 'aba')	The solution handles the alternating distances correctly.
Very long word (approaching maximum string length)	The linear time complexity O(n) where n is word length should be efficient enough.
Word contains non-lowercase alphabets	Convert non-lowercase characters to lowercase before processing to prevent incorrect index calculation; if non-lowercase characters are disallowed, throw an exception.

Null or empty word

How to Handle:

Return 0 as no time is needed to type an empty word.

Word with only one character

How to Handle:

Return the absolute difference between the starting position 'a' and the single character.

Word with all identical characters

How to Handle:

The solution correctly calculates the time based on the repetitive character.

Word with characters in increasing alphabetical order (e.g., 'abc')

How to Handle:

The solution should efficiently calculate the sum of consecutive differences, which are all 1.

Word with characters in decreasing alphabetical order (e.g., 'cba')

How to Handle:

The solution correctly calculates the sum of consecutive differences.

Word with characters oscillating back and forth (e.g., 'aba')

How to Handle:

The solution handles the alternating distances correctly.

Very long word (approaching maximum string length)

How to Handle:

The linear time complexity O(n) where n is word length should be efficient enough.

Word contains non-lowercase alphabets

How to Handle:

Convert non-lowercase characters to lowercase before processing to prevent incorrect index calculation; if non-lowercase characters are disallowed, throw an exception.