Minimum Time to Visit a Cell In a Grid

Hard

Atlassian

3 views

Topics:

GraphsGreedy Algorithms

You are given a m x n matrix grid consisting of non-negative integers where grid[row][col] represents the minimum time required to be able to visit the cell (row, col), which means you can visit the cell (row, col) only when the time you visit it is greater than or equal to grid[row][col].

You are standing in the top-left cell of the matrix in the 0^th second, and you must move to any adjacent cell in the four directions: up, down, left, and right. Each move you make takes 1 second.

Return the minimum time required in which you can visit the bottom-right cell of the matrix. If you cannot visit the bottom-right cell, then return -1.

Example 1:

Input: grid = [[0,1,3,2],[5,1,2,5],[4,3,8,6]]
Output: 7
Explanation: One of the paths that we can take is the following:
- at t = 0, we are on the cell (0,0).
- at t = 1, we move to the cell (0,1). It is possible because grid[0][1] <= 1.
- at t = 2, we move to the cell (1,1). It is possible because grid[1][1] <= 2.
- at t = 3, we move to the cell (1,2). It is possible because grid[1][2] <= 3.
- at t = 4, we move to the cell (1,1). It is possible because grid[1][1] <= 4.
- at t = 5, we move to the cell (1,2). It is possible because grid[1][2] <= 5.
- at t = 6, we move to the cell (1,3). It is possible because grid[1][3] <= 6.
- at t = 7, we move to the cell (2,3). It is possible because grid[2][3] <= 7.
The final time is 7. It can be shown that it is the minimum time possible.

Example 2:

Input: grid = [[0,2,4],[3,2,1],[1,0,4]]
Output: -1
Explanation: There is no path from the top left to the bottom-right cell.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 10⁵
0 <= grid[i][j] <= 10⁵
grid[0][0] == 0

Minimum Time to Visit a Cell In a Grid

Hard

Atlassian

3 views

Topics:

GraphsGreedy Algorithms

You are given a m x n matrix grid consisting of non-negative integers where grid[row][col] represents the minimum time required to be able to visit the cell (row, col), which means you can visit the cell (row, col) only when the time you visit it is greater than or equal to grid[row][col].

You are standing in the top-left cell of the matrix in the 0^th second, and you must move to any adjacent cell in the four directions: up, down, left, and right. Each move you make takes 1 second.

Return the minimum time required in which you can visit the bottom-right cell of the matrix. If you cannot visit the bottom-right cell, then return -1.

Example 1:

Input: grid = [[0,1,3,2],[5,1,2,5],[4,3,8,6]]
Output: 7
Explanation: One of the paths that we can take is the following:
- at t = 0, we are on the cell (0,0).
- at t = 1, we move to the cell (0,1). It is possible because grid[0][1] <= 1.
- at t = 2, we move to the cell (1,1). It is possible because grid[1][1] <= 2.
- at t = 3, we move to the cell (1,2). It is possible because grid[1][2] <= 3.
- at t = 4, we move to the cell (1,1). It is possible because grid[1][1] <= 4.
- at t = 5, we move to the cell (1,2). It is possible because grid[1][2] <= 5.
- at t = 6, we move to the cell (1,3). It is possible because grid[1][3] <= 6.
- at t = 7, we move to the cell (2,3). It is possible because grid[2][3] <= 7.
The final time is 7. It can be shown that it is the minimum time possible.

Example 2:

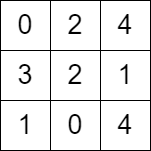
Input: grid = [[0,2,4],[3,2,1],[1,0,4]]
Output: -1
Explanation: There is no path from the top left to the bottom-right cell.

Constraints:

m == grid.length
n == grid[i].length
2 <= m, n <= 1000
4 <= m * n <= 10⁵
0 <= grid[i][j] <= 10⁵
grid[0][0] == 0

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the grid dimensions (number of rows and columns)?
What is the range of possible values for grid[i][j]? Can grid values be negative?
If it's impossible to reach the bottom-right cell (n-1, m-1), what should the function return? Should I return -1 or some other specific value?
Is the starting cell (0, 0) always guaranteed to have a time requirement that allows immediate entry (i.e., grid[0][0] <= 0)?
Are all grid values non-negative integers?

Brute Force Solution

Approach

Imagine you are physically moving through the grid. The brute force method is like trying every single possible path you could take, one at a time, to reach the destination cell. It's incredibly thorough and explores all options.

Here's how the algorithm would work step-by-step:

Start at the beginning cell.
From there, try moving to every cell that is directly next to you (up, down, left, or right).
For each of those new cells, again try moving to every cell that is directly next to them. Keep track of the time it takes to get to each of these cells.
Continue this process, exploring every possible path outward from the starting cell, recording the time at which each cell is visited.
Keep track of the earliest time at which you arrive at the destination cell for each possible path you explore.
After exploring every single path, compare the earliest arrival times you recorded for the destination cell.
The smallest of those times is the minimum time required to visit the destination cell.

Code Implementation

def minimum_time_to_visit_all_cells_brute_force(grid):
    rows = len(grid)
    columns = len(grid[0])
    minimum_time = float('inf')

    def explore(row_index, column_index, current_time):
        nonlocal minimum_time

        # If we have reached the destination, update minimum time
        if row_index == rows - 1 and column_index == columns - 1:
            minimum_time = min(minimum_time, current_time)
            return

        # If we have gone out of bounds, stop exploring
        if row_index < 0 or row_index >= rows or column_index < 0 or column_index >= columns:
            return

        wait_time = 0

        # If we need to wait before entering the cell
        if grid[row_index][column_index] > current_time:
            wait_time = grid[row_index][column_index] - current_time

        new_time = current_time + wait_time + 1

        # Explore adjacent cells
        explore(row_index + 1, column_index, new_time)

        explore(row_index - 1, column_index, new_time)

        explore(row_index, column_index + 1, new_time)

        explore(row_index, column_index - 1, new_time)

    # Start exploring from the top-left cell with time 0
    explore(0, 0, 0)

    #If the final result hasn't been modified, it's unreachable
    if minimum_time == float('inf'):
        return -1
    else:
        return minimum_time

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(4^(m*n)) – The brute force approach explores every possible path from the starting cell (0, 0) to the destination cell (m-1, n-1) by considering all possible moves (up, down, left, right) at each cell. In the worst case, each cell can have up to four possible moves, and we are exploring paths of length proportional to m*n, where m and n are the dimensions of the grid. This leads to an exponential number of paths that could be 4^(m*n). Therefore the time complexity becomes O(4^(m*n)).

Space Complexity

O(N^2) – The brute force approach, as described, explores every possible path. To keep track of the earliest time each cell is visited, it implicitly uses a grid of the same dimensions as the input grid to store these times. Therefore, the auxiliary space required is proportional to the number of cells in the grid, which is N^2, where N is the number of rows/columns in the grid. We also maintain a queue or stack (implicitly through recursion) to manage the cells to visit, which in the worst case, can grow to the size of the entire grid. Thus, the space complexity is O(N^2).

Optimal Solution

Approach

We need to find the fastest way through a grid, where each cell has a minimum time we must reach it. We'll use a path-finding approach that prioritizes cells we can reach soonest, while also respecting the minimum time required for each cell. This method is better than trying every path because it focuses on the most promising routes first.

Here's how the algorithm would work step-by-step:

Start at the beginning of the grid.
Keep track of the earliest time you can reach each cell.
Consider all the neighboring cells you can move to from your current location.
For each neighbor, calculate the time it would take to reach it from your current location. Remember that you might have to wait at the current location to meet the minimum time requirement for the neighbor.
Update the earliest arrival time for the neighbor if the newly calculated time is earlier than the currently recorded earliest time.
Choose the neighbor with the overall earliest possible arrival time that hasn't been visited yet.
Repeat steps 3-6 until you reach the destination cell or there are no more reachable cells.

Code Implementation

import heapq

def minimum_time_to_visit_all_cells(grid):
    rows = len(grid)
    columns = len(grid[0])
    earliest_arrival_time = [[float('inf')] * columns for _ in range(rows)]
    earliest_arrival_time[0][0] = 0
    priority_queue = [(0, 0, 0)]
    visited = set()

    while priority_queue:
        time, row, column = heapq.heappop(priority_queue)

        if (row, column) in visited:
            continue
        visited.add((row, column))

        if row == rows - 1 and column == columns - 1:
            return time

        # Explore neighboring cells
        for delta_row, delta_column in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
            new_row = row + delta_row
            new_column = column + delta_column

            if 0 <= new_row < rows and 0 <= new_column < columns:
                
                wait_time = grid[new_row][new_column] - time - 1

                # Ensure we meet the minimum time requirement
                next_time = time + 1 if wait_time <= 0 else time + 1 + wait_time
                
                #Update arrival time if a shorter path is found
                if next_time < earliest_arrival_time[new_row][new_column]:
                    earliest_arrival_time[new_row][new_column] = next_time

                    # Add new location to priority queue
                    heapq.heappush(priority_queue, (next_time, new_row, new_column))

    return -1

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m * n * log(m * n)) – The algorithm uses a priority queue (heap) to find the cell with the earliest possible arrival time, where m and n represent the dimensions of the grid. In the worst case, we might add each cell to the priority queue. Adding and extracting from the priority queue takes O(log(m * n)) time. We explore neighbors from each cell, and in the worst-case scenario, we might visit all m * n cells. Therefore, the overall time complexity is dominated by the priority queue operations performed for each cell, resulting in O(m * n * log(m * n)). The heap size will not exceed m*n so the log call will reflect this limitation.

Space Complexity

O(M*N) – The algorithm keeps track of the earliest time to reach each cell in the grid, requiring a data structure (e.g., a 2D array) of the same size as the input grid to store these times. We also maintain a priority queue (heap) to efficiently retrieve the neighbor with the earliest possible arrival time. In the worst case, this priority queue could contain all the cells in the grid. Therefore, the auxiliary space used is proportional to the grid's dimensions, which is M*N where M is the number of rows and N is the number of columns. This results in a space complexity of O(M*N).

Edge Cases

Case	How to Handle
Null or empty grid	Return -1 or throw an exception indicating invalid input as no path can be found.
1x1 grid (single cell)	Return 0 if grid[0][0] <= 0, otherwise return grid[0][0] to satisfy wait time constraint.
Start cell requires significant wait time (grid[0][0] > 0)	Ensure the algorithm correctly waits the required time before proceeding from the start cell by incorporating grid[0][0] into the initial time.
Target cell is unreachable (no path exists)	Return -1 after the search space has been exhausted, indicating no possible path.
Large grid size that could lead to timeout or memory issues	Use an efficient algorithm like A* search with a proper heuristic to minimize the search space and time complexity.
Values in grid are very large, leading to potential integer overflow	Use long data type to store the accumulated time to avoid integer overflow during calculations.
Grid contains a 'wall' where it's impossible to move to the adjacent cells due to time constraints	Algorithm correctly waits until the condition ti > grid[ri][ci] is met before moving to that cell.
Multiple possible paths to the target cell with different minimum times	The algorithm should explore all possible paths and return the absolute minimum time to reach the target.