Minimum Weighted Subgraph With the Required Paths
HardYou are given an integer n denoting the number of nodes of a weighted directed graph. The nodes are numbered from 0 to n - 1.
You are also given a 2D integer array edges where edges[i] = [fromi, toi, weighti] denotes that there exists a directed edge from fromi to toi with weight weighti.
Lastly, you are given three distinct integers src1, src2, and dest denoting three distinct nodes of the graph.
Return the minimum weight of a subgraph of the graph such that it is possible to reach dest from both src1 and src2 via a set of edges of this subgraph. In case such a subgraph does not exist, return -1.
A subgraph is a graph whose vertices and edges are subsets of the original graph. The weight of a subgraph is the sum of weights of its constituent edges.
Example 1:
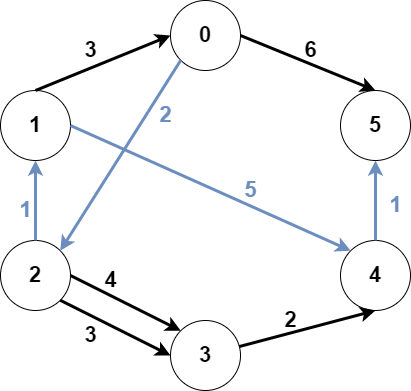
Input: n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5 Output: 9 Explanation: The above figure represents the input graph. The blue edges represent one of the subgraphs that yield the optimal answer. Note that the subgraph [[1,0,3],[0,5,6]] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
Example 2:

Input: n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2 Output: -1 Explanation: The above figure represents the input graph. It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
Constraints:
3 <= n <= 1050 <= edges.length <= 105edges[i].length == 30 <= fromi, toi, src1, src2, dest <= n - 1fromi != toisrc1,src2, anddestare pairwise distinct.1 <= weight[i] <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the number of nodes (N) and edges (M) in the graph? What are the possible ranges for the edge weights?
- What data types are used for the node IDs and edge weights (e.g., integers, floats)? Can edge weights be negative or zero?
- If it's impossible to find a subgraph containing paths from source1 to target1 AND source2 to target2, what should the function return? Should I return null, an empty graph representation, or a specific error code?
- Are the source and target nodes (source1, target1, source2, target2) guaranteed to be distinct? Are source1 and source2 allowed to be the same node, or target1 and target2?
- If multiple minimum weighted subgraphs satisfy the required paths, is any one of them acceptable, or is there a specific criterion for choosing between them?
Brute Force Solution
Approach
The brute force strategy to find the minimum weighted subgraph with required paths involves exploring all possible subgraphs of the original graph. We systematically check if each subgraph satisfies the path requirements and, if so, calculate its weight. Finally, we select the subgraph with the minimum weight among those that meet the requirements.
Here's how the algorithm would work step-by-step:
- Consider all possible combinations of edges from the original graph. Each combination represents a potential subgraph.
- For each subgraph, verify if it contains all the required paths between the specified pairs of nodes. This means checking if there's a valid route from each source node to its corresponding destination node within the subgraph.
- If a subgraph contains all the required paths, calculate its total weight by summing the weights of all the edges included in that subgraph.
- Keep track of the weight for all subgraphs that contain the required paths.
- After checking all possible subgraphs, identify the subgraph with the smallest total weight among those that satisfy the path requirements. This subgraph is the minimum weighted subgraph with the required paths.
Code Implementation
def minimum_weighted_subgraph_brute_force(graph, required_paths):
edges = list(graph.keys())
number_of_edges = len(edges)
minimum_weight = float('inf')
best_subgraph = None
# Iterate through all possible subgraphs
for i in range(2**number_of_edges):
subgraph = {}
subgraph_weight = 0
for j in range(number_of_edges):
if (i >> j) & 1:
edge = edges[j]
subgraph[edge] = graph[edge]
subgraph_weight += graph[edge]
# Check if the subgraph contains all required paths
all_paths_present = True
for start_node, end_node in required_paths:
if not path_exists(subgraph, start_node, end_node):
all_paths_present = False
break
if all_paths_present:
# Update minimum weight if this subgraph is better
if subgraph_weight < minimum_weight:
minimum_weight = subgraph_weight
best_subgraph = subgraph
return best_subgraph
def path_exists(graph, start_node, end_node):
visited = set()
queue = [start_node]
while queue:
node = queue.pop(0)
if node == end_node:
return True
if node in visited:
continue
visited.add(node)
for edge, weight in graph.items():
if edge[0] == node:
queue.append(edge[1])
return FalseBig(O) Analysis
Optimal Solution
Approach
We need to find the smallest possible combined weight of paths that satisfy certain route requirements in a network. The best approach cleverly combines shortest path calculations and carefully considers how to combine these paths to minimize overall weight.
Here's how the algorithm would work step-by-step:
- First, we need to figure out the shortest route between each pair of important locations in the network. We can use a well-known algorithm for finding the shortest path between all pairs of locations.
- Next, for each required route, use the shortest path calculated earlier. This gives us a collection of paths.
- The tricky part is that some paths might share edges, and we only want to pay for those shared edges once. We can visualize this as needing to 'merge' overlapping paths to remove redundancy.
- We then analyze the set of paths and identify the shared edges. For each shared edge, we only count its weight once when calculating the total weight of the required subgraph.
- A systematic way to find the minimum combined weight is to think of this as a flow problem where we are routing certain amounts of flow between specified nodes, and looking for the minimum cost to support the required flow.
- An important insight is that because we have already computed all pairwise shortest paths, we only need to consider each edge a small number of times - we are not doing an exhaustive search.
- The final combined weight of the paths is the minimum possible weight of the subgraph that includes all the necessary routes.
Code Implementation
import heapq
def solve_min_weighted_subgraph(
number_of_nodes,
edges,
required_paths
):
# Calculate all-pairs shortest paths using Floyd-Warshall algorithm.
shortest_paths = floyd_warshall(number_of_nodes, edges)
all_edges_in_shortest_paths = set()
# Collect edges from all required shortest paths.
for start_node, end_node in required_paths:
path = reconstruct_path(start_node, end_node, shortest_paths[1])
for i in range(len(path) - 1):
all_edges_in_shortest_paths.add(tuple(sorted((path[i], path[i + 1]))))
# Calculate total weight of the edges in the subgraph
total_weight = 0
for start_node, end_node, weight in edges:
if tuple(sorted((start_node, end_node))) in all_edges_in_shortest_paths:
total_weight += weight
return total_weight
def floyd_warshall(number_of_nodes, edges):
distance = {
(i, j): float('inf') if i != j else 0
for i in range(number_of_nodes)
for j in range(number_of_nodes)
}
predecessor = {
(i, j): None for i in range(number_of_nodes) for j in range(number_of_nodes)
}
for start_node, end_node, weight in edges:
distance[(start_node, end_node)] = weight
distance[(end_node, start_node)] = weight
predecessor[(start_node, end_node)] = start_node
predecessor[(end_node, start_node)] = end_node
for intermediate_node in range(number_of_nodes):
for start_node in range(number_of_nodes):
for end_node in range(number_of_nodes):
new_distance = (
distance[(start_node, intermediate_node)]
+ distance[(intermediate_node, end_node)]
)
if new_distance < distance[(start_node, end_node)]:
distance[(start_node, end_node)] = new_distance
predecessor[(start_node, end_node)] = predecessor[(intermediate_node, end_node)] if predecessor[(intermediate_node, end_node)] is not None else intermediate_node
return distance, predecessor
def reconstruct_path(start_node, end_node, predecessor):
# Reconstruct the path from the predecessor matrix.
path = [end_node]
current_node = end_node
while current_node != start_node:
found_predecessor = False
for node in range(len(predecessor)):
if predecessor[(node,current_node)] == current_node:
continue
if predecessor[(node,current_node)] is not None:
previous_node = node
path.append(previous_node)
current_node = previous_node
found_predecessor = True
break
if not found_predecessor:
return []
return path[::-1]Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty graph (no nodes or edges) | Return -1 if the graph is empty since no subgraph can be formed. |
| No path exists between the source and destination nodes for either required path. | Return -1 if either Dijkstra's algorithm returns infinity, indicating no path exists. |
| Source node is the same as the destination node for either required path. | Handle by returning 0 cost if the source is the destination after checking for other conditions. |
| Graph with only one node. | If source and destination are the same node then cost is 0, otherwise return -1. |
| Graph with negative edge weights (if Dijkstra's is used directly) | Use Bellman-Ford instead of Dijkstra's or Johnson's algorithm to handle negative weights if allowed; otherwise, indicate input is invalid. |
| Integer overflow in edge weight accumulation. | Use a larger data type (e.g., long) or check for overflow during edge weight summation. |
| Graph contains cycles. | Dijkstra's can handle cycles if there is no negative edge, however negative cycles needs Bellman-Ford or Johnson's algortihm. |
| Disconnected graph where not all nodes are reachable from start nodes. | Dijkstra's will appropriately return infinity for unreachable nodes ensuring the return value is -1. |