Network Delay Time #18 Most Asked
MediumYou are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.
We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.
Example 1:
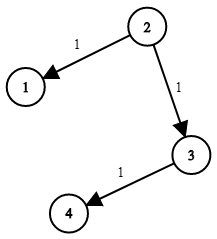
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 Output: 2
Example 2:
Input: times = [[1,2,1]], n = 2, k = 1 Output: 1
Example 3:
Input: times = [[1,2,1]], n = 2, k = 2 Output: -1
Constraints:
1 <= k <= n <= 1001 <= times.length <= 6000times[i].length == 31 <= ui, vi <= nui != vi0 <= wi <= 100- All the pairs
(ui, vi)are unique. (i.e., no multiple edges.)
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on `n`, the number of nodes, and the weight `w` of the edges in `times`?
- Is it possible for the graph to be disconnected? If so, what should be the return value in that case?
- Can there be multiple edges between the same two nodes with different weights? If so, should I consider the minimum weight or handle them in some other way?
- Is it guaranteed that the starting node `k` is a valid node within the range of 1 to `n`?
- If a node is unreachable from the starting node `k`, should it still be included when checking if all nodes have received the signal?
Brute Force Solution
Approach
The brute-force approach to finding the maximum time it takes for a signal to reach all nodes in a network involves exploring all possible paths from the starting node. We essentially try out every route and track the time it takes. Then, we determine the longest time required to reach all nodes.
Here's how the algorithm would work step-by-step:
- Begin by exploring all direct paths from the starting node to its immediate neighbors.
- For each neighbor, find the time it takes to reach them directly from the starting node.
- From each of those neighbors, explore all paths to their neighbors, calculating the cumulative time from the starting node.
- Keep repeating this process, branching out to all possible nodes and recording the time it takes to reach each node from the starting point through various routes.
- If a node can be reached through multiple paths, remember to track the time it takes for each of those paths.
- After exploring all possible paths, find the shortest time required to reach each node.
- Once you have the shortest time to reach each node, identify the maximum of these times. This maximum time represents the longest it takes for the signal to reach every node from the starting node.
Code Implementation
def network_delay_time_brute_force(times, number_of_nodes, start_node):
all_paths_times = {node: float('inf') for node in range(1, number_of_nodes + 1)}
all_paths_times[start_node] = 0
# Iterate through each possible path
for _ in range(number_of_nodes):
for source_node, destination_node, travel_time in times:
total_time = all_paths_times[source_node] + travel_time
# Update shortest time for a node
if total_time < all_paths_times[destination_node]:
all_paths_times[destination_node] = total_time
maximum_travel_time = 0
for node in range(1, number_of_nodes + 1):
#If node is unreachable, return -1
if all_paths_times[node] == float('inf'):
return -1
maximum_travel_time = max(maximum_travel_time, all_paths_times[node])
return maximum_travel_timeBig(O) Analysis
Optimal Solution
Approach
We want to find the fastest time it takes for a signal to reach everyone in a network. The key is to explore the network in order of increasing travel time, always choosing the quickest path to each person.
Here's how the algorithm would work step-by-step:
- Start at the source node and mark its time as zero.
- Keep track of the shortest time it takes to reach each person from the source.
- Consider all direct connections from the source. Update the shortest time to a person if the new path is faster than the current fastest path to that person.
- Move to the person closest to the source, who now has a determined shortest time. Repeat the process, considering all connections from this person and potentially updating the shortest times to other people.
- Continue this process of exploring from the closest people, updating times as needed, until you have visited every person or there are no more updates to be made.
- After this process is finished, find the longest of the shortest times. If this longest time is finite, that is the answer. If not, this means the signal couldn't reach everyone so we have no solution.
Code Implementation
import heapq
def network_delay_time(times, number_of_nodes, source_node):
adjacency_list = [[] for _ in range(number_of_nodes + 1)]
for source, destination, travel_time in times:
adjacency_list[source].append((destination, travel_time))
shortest_times = {node: float('inf') for node in range(1, number_of_nodes + 1)}
shortest_times[source_node] = 0
priority_queue = [(0, source_node)]
while priority_queue:
current_travel_time, current_node = heapq.heappop(priority_queue)
# If current path is slower, skip
if current_travel_time > shortest_times[current_node]:
continue
for neighbor, time_to_neighbor in adjacency_list[current_node]:
new_travel_time = current_travel_time + time_to_neighbor
# Update if a shorter path is found
if new_travel_time < shortest_times[neighbor]:
shortest_times[neighbor] = new_travel_time
heapq.heappush(priority_queue, (new_travel_time, neighbor))
max_travel_time = max(shortest_times.values())
# Check if all nodes are reachable
if max_travel_time == float('inf'):
return -1
return max_travel_timeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty times array | If there are no edges, and n > 0, check if k is valid node; if not return -1, else return 0 if n is 1, otherwise return -1. |
| n = 1 (single node), times is empty | If there's only one node and no edges, the time to reach all nodes is 0. |
| k is an invalid node (k < 1 or k > n) | Return -1 immediately since the starting node is outside the valid range. |
| Graph is disconnected and some nodes are unreachable from k | After running Dijkstra or similar algorithm, check if the distance to all nodes is infinity; if so, return -1. |
| Graph contains cycles | Dijkstra's algorithm correctly handles cycles by always choosing the shortest path discovered so far. |
| Large n and large edge weights causing integer overflow | Use long data types to store distances to prevent overflow during calculations. |
| All edges have weight 0 | Dijkstra's algorithm will work if implemented correctly by choosing the node with lowest cost; special case not needed. |
| Times array is very large, causing memory issues | Consider alternative graph representations or algorithms with lower memory footprint; in Python, garbage collection may help but large arrays may still cause issues. |