Number of Increasing Paths in a Grid
HardYou are given an m x n integer matrix grid, where you can move from a cell to any adjacent cell in all 4 directions.
Return the number of strictly increasing paths in the grid such that you can start from any cell and end at any cell. Since the answer may be very large, return it modulo 109 + 7.
Two paths are considered different if they do not have exactly the same sequence of visited cells.
Example 1:
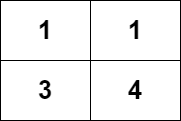
Input: grid = [[1,1],[3,4]] Output: 8 Explanation: The strictly increasing paths are: - Paths with length 1: [1], [1], [3], [4]. - Paths with length 2: [1 -> 3], [1 -> 4], [3 -> 4]. - Paths with length 3: [1 -> 3 -> 4]. The total number of paths is 4 + 3 + 1 = 8.
Example 2:
Input: grid = [[1],[2]] Output: 3 Explanation: The strictly increasing paths are: - Paths with length 1: [1], [2]. - Paths with length 2: [1 -> 2]. The total number of paths is 2 + 1 = 3.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 1051 <= grid[i][j] <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid (number of rows and columns), and what is the maximum size we should expect for each dimension?
- What is the range of possible elevation values within the grid's cells? Can the values be negative or zero?
- If the grid is empty (either zero rows or zero columns), what value should I return?
- Can you clarify what constitutes a 'path'? Does it need to be contiguous in terms of grid coordinates, or just strictly increasing in elevation?
- Should I be concerned about integer overflow when calculating the total number of paths, given that I need to return the result modulo 10^9 + 7?
Brute Force Solution
Approach
The brute force approach to finding increasing paths in a grid involves exploring every possible path, one by one. We start from each cell and see where we can go, always looking for a larger number. We repeat this process until we've exhausted all possible paths from every starting cell.
Here's how the algorithm would work step-by-step:
- Consider each cell in the grid as a potential starting point for a path.
- From the starting cell, look at its neighbors (up, down, left, right).
- For each neighbor, check if the number in that neighboring cell is larger than the number in the current cell.
- If a neighbor has a larger number, move to that neighbor and extend the path. If not, ignore that neighbor.
- Repeat the process of looking for larger neighbors from the new cell, extending the path further.
- Continue extending the path until you reach a point where there are no larger neighbors to move to (this is the end of a path).
- Record this path as a valid increasing path.
- Go back to the starting cell and explore all other possible paths by choosing different neighbors with larger numbers.
- Repeat this whole process for every single cell in the grid, treating each as a potential starting point.
- Count all the recorded valid increasing paths to get the total number of increasing paths in the grid.
Code Implementation
def number_of_increasing_paths_brute_force(grid):
rows = len(grid)
cols = len(grid[0])
total_paths = 0
def find_paths(row, col):
path_count = 1
# Define possible movements: up, down, left, right
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
for direction_row_change, direction_col_change in directions:
new_row = row + direction_row_change
new_col = col + direction_col_change
if 0 <= new_row < rows and 0 <= new_col < cols and \
grid[new_row][new_col] > grid[row][col]:
# Recursively extend the path
path_count += find_paths(new_row, new_col)
return path_count
# Iterate through all starting positions
for row in range(rows):
for col in range(cols):
total_paths += find_paths(row, col)
return total_pathsBig(O) Analysis
Optimal Solution
Approach
To efficiently count the paths, we'll use a clever trick to remember previously calculated results and avoid redundant work. We explore the grid in a specific order to ensure that when we reach a cell, we already know the number of increasing paths starting from its neighbors.
Here's how the algorithm would work step-by-step:
- Sort all the numbers in the grid from smallest to largest. This will determine the order in which we process each position.
- For each number (starting with the smallest), find its location in the grid.
- For each location, look at its neighbors (up, down, left, and right).
- If a neighbor has a larger number than the current location's number, it means we can extend an increasing path to that neighbor.
- Take the number of paths that start from that neighbor (which we've already calculated because we sorted the numbers) and add it to the number of paths starting from the current location.
- Remember the number of paths starting from the current location so we can use it later when considering its neighbors.
- Keep doing this for all the numbers, from smallest to largest.
- At the end, add up the number of paths starting from each location to get the total number of increasing paths in the grid.
Code Implementation
def number_of_increasing_paths(grid):
rows = len(grid)
cols = len(grid[0])
path_counts = [[0] * cols for _ in range(rows)]
MOD = 10**9 + 7
# Store each cell's value and its coordinates.
cell_values = []
for row_index in range(rows):
for col_index in range(cols):
cell_values.append((grid[row_index][col_index], row_index, col_index))
# Sort cells based on their values in descending order.
cell_values.sort(reverse=True)
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
for _, row_index, col_index in cell_values:
# Each cell has at least one path: itself.
path_counts[row_index][col_index] = 1
# Iterate over possible directions to find neighbors.
for direction_row, direction_col in directions:
new_row = row_index + direction_row
new_col = col_index + direction_col
#Check boundaries and increasing path
if 0 <= new_row < rows and 0 <= new_col < cols and grid[new_row][new_col] > grid[row_index][col_index]:
# Accumulate path counts from valid neighbors.
path_counts[row_index][col_index] += path_counts[new_row][new_col]
path_counts[row_index][col_index] %= MOD
total_paths = 0
# Sum up all individual path counts to obtain the total.
for row_index in range(rows):
for col_index in range(cols):
total_paths += path_counts[row_index][col_index]
total_paths %= MOD
return total_pathsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return 0 immediately as there are no paths in an empty grid. |
| Grid with a single cell | Return 1, as the single cell itself forms a path of length 1. |
| All cells have the same value | Each cell only forms a path of length 1, so return the number of cells. |
| Grid with only two cells where the second cell is smaller than the first | Each cell is a path of length 1, so return 2. |
| Large grid exceeding memory limits (scalability) | Dynamic programming (memoization) is essential to prevent redundant calculations and improve performance and should ideally be coupled with iterative methods. |
| Grid with negative elevation values | The algorithm should work correctly with negative values as only relative elevation matters for increasing paths. |
| Integer overflow when calculating the number of paths | Apply the modulo operator (10^9 + 7) after each addition to prevent overflow. |
| Grid with maximum integer values | Ensure the chosen data types can handle the maximum integer values defined in the problem constraints. |