Number of Orders in the Backlog #9 Most Asked
MediumYou are given a 2D integer array orders, where each orders[i] = [pricei, amounti, orderTypei] denotes that amounti orders have been placed of type orderTypei at the price pricei. The orderTypei is:
0if it is a batch ofbuyorders, or1if it is a batch ofsellorders.
Note that orders[i] represents a batch of amounti independent orders with the same price and order type. All orders represented by orders[i] will be placed before all orders represented by orders[i+1] for all valid i.
There is a backlog that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:
- If the order is a
buyorder, you look at thesellorder with the smallest price in the backlog. If thatsellorder's price is smaller than or equal to the currentbuyorder's price, they will match and be executed, and thatsellorder will be removed from the backlog. Else, thebuyorder is added to the backlog. - Vice versa, if the order is a
sellorder, you look at thebuyorder with the largest price in the backlog. If thatbuyorder's price is larger than or equal to the currentsellorder's price, they will match and be executed, and thatbuyorder will be removed from the backlog. Else, thesellorder is added to the backlog.
Return the total amount of orders in the backlog after placing all the orders from the input. Since this number can be large, return it modulo 109 + 7.
Example 1:
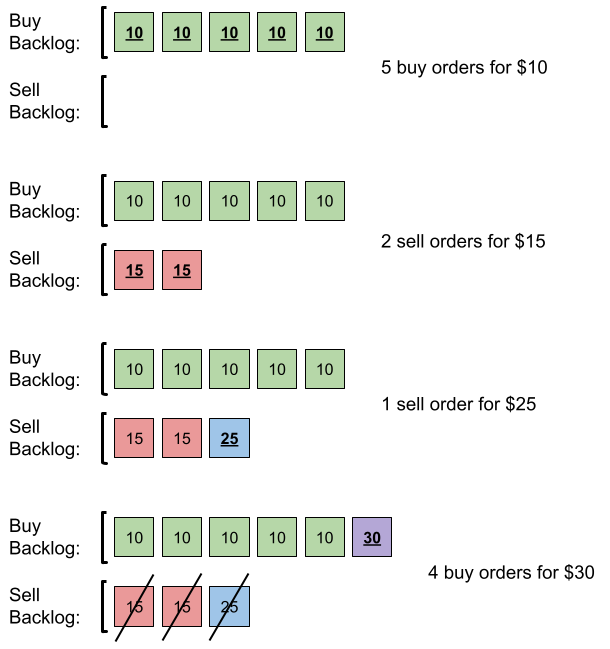
Input: orders = [[10,5,0],[15,2,1],[25,1,1],[30,4,0]] Output: 6 Explanation: Here is what happens with the orders: - 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog. - 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog. - 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog. - 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4th order is added to the backlog. Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.
Example 2:
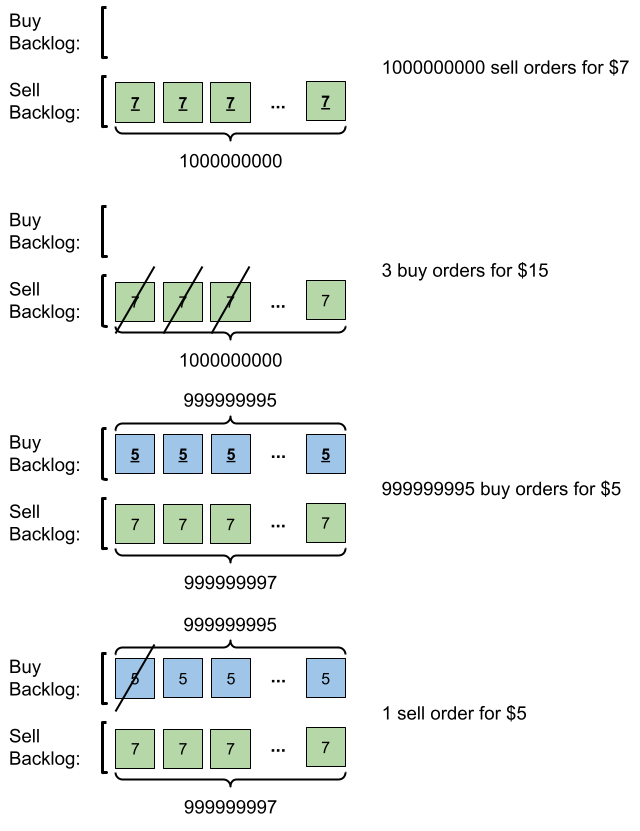
Input: orders = [[7,1000000000,1],[15,3,0],[5,999999995,0],[5,1,1]] Output: 999999984 Explanation: Here is what happens with the orders: - 109 orders of type sell with price 7 are placed. There are no buy orders, so the 109 orders are added to the backlog. - 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog. - 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog. - 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog. Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (109 + 7).
Constraints:
1 <= orders.length <= 105orders[i].length == 31 <= pricei, amounti <= 109orderTypeiis either0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the size of the `orders` and `queries` arrays, and the ranges for `price`, `amount`, and `orderType` within each tuple?
- If an order in `queries` can be completely fulfilled by the backlog, should it be removed from the `queries` array or completely processed and then removed?
- If a buy order matches multiple sell orders in the backlog, should I prioritize the sell order with the lowest price, and vice-versa for sell orders matching buy orders?
- What should I do if there are invalid inputs, such as a negative `amount` or an `orderType` other than 0 or 1? Should I throw an error or handle it in some other way?
- After processing all queries, should I consider the orders array as the final backlog, or should I consider the backlog as a separate data structure that I have built up during the processing of the queries?
Brute Force Solution
Approach
To find the total number of orders in the backlog, we'll consider fulfilling the orders one by one. The brute force approach involves exploring all possible sequences of fulfilling the given orders and then summing up their respective counts based on the problem's specific constraints.
Here's how the algorithm would work step-by-step:
- Start by examining the first order in the list.
- Consider fulfilling this first order immediately.
- Then, consider fulfilling the second order immediately after the first and so on until all possible permutations are exhausted.
- For each of these order arrangements, calculate whether the backlog is valid based on the problem constraints. This involves checking if fulfilling the orders in that specific sequence satisfies conditions, such as the maximum allowable order quantity.
- If the order sequence is valid, add one to the total number of valid backlog sequences.
- Repeat this process for every possible order of fulfilling all the given orders, carefully tracking and summing the number of arrangements that lead to a valid backlog.
- The final sum will represent the total number of possible orders that can exist in the backlog.
Code Implementation
def number_of_backlog_orders_brute_force(requests):
number_of_valid_orders = 0
import itertools
# Consider all possible orderings of the requests
for order in itertools.permutations(requests):
if is_valid_order(order):
number_of_valid_orders += 1
return number_of_valid_orders
def is_valid_order(order):
stock = 0
for request_type, quantity, due_date in order:
# Simulate the process of fulfilling the requests in that specific order
if request_type == 'buy':
stock += quantity
elif request_type == 'sell':
# Check if a sell order arrives before there is sufficient stock
if stock < quantity:
return False
stock -= quantity
else:
return False
return TrueBig(O) Analysis
Optimal Solution
Approach
The problem asks us to simulate processing orders and determining how many stay in a backlog. We'll efficiently keep track of the orders and how many can be fulfilled at each step. The key is to fulfill as many orders as possible at each step without going over the limit.
Here's how the algorithm would work step-by-step:
- Go through each order one at a time.
- For each order, check if the quantity can be completely fulfilled by the current supply.
- If it can, subtract the order quantity from the supply and move to the next order.
- If it cannot, fulfill as much of the order as possible by setting the supply to zero.
- The remaining quantity of that order then goes into the backlog, and you add the *unfulfilled* amount back to the order details for the next step.
- After processing all orders, add up all the remaining quantities of orders in your backlog to find the total backlog size.
Code Implementation
import heapq
def number_of_orders_in_backlog(
orders: list[list[int]], processing_capacities: list[int]
) -> int:
backlog = []
total_unprocessed_orders = 0
for day, daily_capacity in enumerate(processing_capacities):
# Add new orders to the backlog, organizing by priority.
for order_amount, order_priority in orders[day]:
heapq.heappush(backlog, (order_priority, order_amount))
total_unprocessed_orders += order_amount
# Process orders based on priority, up to daily capacity.
while daily_capacity > 0 and backlog:
order_priority, order_amount = heapq.heappop(backlog)
# If we can fulfill the whole order, do so.
if order_amount <= daily_capacity:
daily_capacity -= order_amount
total_unprocessed_orders -= order_amount
else:
# Otherwise, fulfill as much as possible.
total_unprocessed_orders -= daily_capacity
order_amount -= daily_capacity
daily_capacity = 0
# Re-add the remaining order to the backlog.
heapq.heappush(backlog, (order_priority, order_amount))
# At the end, return the number of orders left in the backlog.
return total_unprocessed_ordersBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty orders and queries arrays | Return 0 since the initial backlog is empty and no orders are added. |
| Large amount values in orders/queries that cause intermediate overflows | Use modulo operator after each addition/subtraction to prevent integer overflow. |
| Price is 0 in orders/queries | Treat zero price as valid, matching with other orders with a price of 0 based on orderType. |
| Orders and queries contain extreme values for price and amount near the maximum integer value | The modulo operator should handle this as long as intermediate calculations do not exceed maximum integer bounds *before* the modulo is applied. |
| A query completely depletes an order in the backlog and also consumes a fraction of the next order. | Correctly update backlog, removing completed orders and reducing amount of partially filled orders. |
| Queries continuously adding to the backlog without any matches | Backlog data structures must be capable of storing large numbers of orders efficiently. |
| Queries that perfectly match all existing orders in the backlog, emptying the backlog completely. | Handle empty backlog scenario after matching all queries. |
| OrderType is an invalid value (not 0 or 1). | Explicitly handle invalid orderType values by throwing an exception or ignoring them based on problem specifications. |