Number of Possible Sets of Closing Branches
Hard
1 view
Topics:
GraphsBit Manipulation
There is a company with n branches across the country, some of which are connected by roads. Initially, all branches are reachable from each other by traveling some roads.
The company has realized that they are spending an excessive amount of time traveling between their branches. As a result, they have decided to close down some of these branches (possibly none). However, they want to ensure that the remaining branches have a distance of at most maxDistance from each other.
The distance between two branches is the minimum total traveled length needed to reach one branch from another.
You are given integers n, maxDistance, and a 0-indexed 2D array roads, where roads[i] = [ui, vi, wi] represents the undirected road between branches ui and vi with length wi.
Return the number of possible sets of closing branches, so that any branch has a distance of at most maxDistance from any other.
Note that, after closing a branch, the company will no longer have access to any roads connected to it.
Note that, multiple roads are allowed.
Example 1:
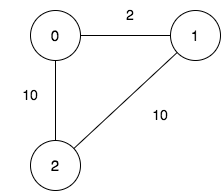
Input: n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]] Output: 5 Explanation: The possible sets of closing branches are: - The set [2], after closing, active branches are [0,1] and they are reachable to each other within distance 2. - The set [0,1], after closing, the active branch is [2]. - The set [1,2], after closing, the active branch is [0]. - The set [0,2], after closing, the active branch is [1]. - The set [0,1,2], after closing, there are no active branches. It can be proven, that there are only 5 possible sets of closing branches.
Example 2:
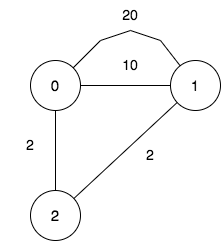
Input: n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]] Output: 7 Explanation: The possible sets of closing branches are: - The set [], after closing, active branches are [0,1,2] and they are reachable to each other within distance 4. - The set [0], after closing, active branches are [1,2] and they are reachable to each other within distance 2. - The set [1], after closing, active branches are [0,2] and they are reachable to each other within distance 2. - The set [0,1], after closing, the active branch is [2]. - The set [1,2], after closing, the active branch is [0]. - The set [0,2], after closing, the active branch is [1]. - The set [0,1,2], after closing, there are no active branches. It can be proven, that there are only 7 possible sets of closing branches.
Example 3:
Input: n = 1, maxDistance = 10, roads = [] Output: 2 Explanation: The possible sets of closing branches are: - The set [], after closing, the active branch is [0]. - The set [0], after closing, there are no active branches. It can be proven, that there are only 2 possible sets of closing branches.
Constraints:
1 <= n <= 101 <= maxDistance <= 1050 <= roads.length <= 1000roads[i].length == 30 <= ui, vi <= n - 1ui != vi1 <= wi <= 1000- All branches are reachable from each other by traveling some roads.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the size of `n` and the number of restrictions?
- Are the branch numbers in the `restrictions` array 1-indexed or 0-indexed?
- Can there be restrictions between a branch and itself (i.e., `restrictions[i] = [x, x]`)?
- If there are no valid sets of closing branches (due to all branches being restricted), what should I return?
- Are the branch numbers in `restrictions` guaranteed to be within the range of 1 to n (or 0 to n-1, depending on the indexing)?
Brute Force Solution
Approach
The brute force approach tries every single possible combination to find the solution. For this particular problem, we'll explore every possible way to arrange the branches and determine which ones are valid sets. This is like trying out all the different ways you could organize your books on a shelf to see which arrangements fit and look the best.
Here's how the algorithm would work step-by-step:
- Imagine each branch can either be part of the final set or not.
- Start by considering all the branches. Pick the first branch.
- Explore the case where it's IN the set, and the case where it's NOT in the set.
- For each of those possibilities, move to the second branch and again, consider both cases: IN the set or NOT in the set.
- Continue this process for every branch until you've considered all possible combinations of branches being in or out of the final set.
- After creating each possible combination, check if the resulting set of branches actually meets the requirements for being a 'closing set'.
- If a set meets all the requirements, count it as a valid solution. If not, discard it.
- Once all combinations have been checked, count all the valid solutions you found and that's your answer.
Code Implementation
def number_of_possible_sets_of_closing_branches(branches):
number_of_branches = len(branches)
valid_sets_count = 0
# Iterate through all possible subsets using binary representation.
for i in range(2**number_of_branches):
current_set = []
for j in range(number_of_branches):
# If the j-th bit is set in i, include branches[j] in the current set.
if (i >> j) & 1:
current_set.append(branches[j])
# Check if the current set is a valid closing set
if is_valid_closing_set(current_set):
valid_sets_count += 1
return valid_sets_count
def is_valid_closing_set(branch_set):
if not branch_set:
return True
# Check for overlaps among branches in the set
for i in range(len(branch_set)):
for j in range(i + 1, len(branch_set)):
if overlaps(branch_set[i], branch_set[j]):
return False
return True
def overlaps(branch1, branch2):
start1, end1 = branch1
start2, end2 = branch2
# Check for overlap between the two branches
if (start1 < end2) and (start2 < end1):
return True
else:
return False
Big(O) Analysis
Time Complexity
O(2^n * n) – The algorithm iterates through all possible subsets of the input set of n branches. Generating all subsets takes O(2^n) time, as each branch can either be included or excluded. For each subset, we need to validate if it is a 'closing set', and this validation could take O(n) time in the worst case, as we potentially need to iterate through all branches in the subset to verify its properties. Therefore, the overall time complexity is O(2^n * n).
Space Complexity
O(N) – The described brute force approach utilizes recursion to explore all possible combinations of branches. In the worst-case scenario, each branch is considered independently, leading to a recursion depth proportional to the number of branches, N. Each recursive call requires a new stack frame that stores local variables and the return address. Therefore, the auxiliary space used by the recursion stack grows linearly with N, resulting in a space complexity of O(N).
Optimal Solution
Approach
We are asked to count how many different ways we can form sets of closing branches, where each branch needs to have a matching opening branch. The key is to realize that this problem can be solved using a mathematical sequence related to matched parentheses or well-formed bracket arrangements.
Here's how the algorithm would work step-by-step:
- Recognize that each closing branch must correspond to a previously open branch. This is like pairing up opening and closing parentheses.
- Recall the Catalan numbers, which count the number of ways to form valid sequences of balanced parentheses.
- Realize that the number of valid branch arrangements for a given number of branch pairs is a Catalan number.
- Compute the Catalan number for the given number of branch pairs, this will give you the total number of possible sets of valid closing branches.
- Report the calculated Catalan number as your answer.
Code Implementation
def number_of_possible_sets_of_closing_branches(number_of_branch_pairs):
# Calculate the Catalan number to find the number of valid arrangements.
catalan_number = calculate_catalan_number(number_of_branch_pairs)
return catalan_number
def calculate_catalan_number(input_number):
# The Catalan number is calculated using the formula: C(n) = (2n)! / (n!(n+1)!).
numerator = calculate_factorial(2 * input_number)
denominator = calculate_factorial(input_number) * calculate_factorial(input_number + 1)
# Integer division to match mathematical formula.
return numerator // denominator
def calculate_factorial(number_to_factorial):
if number_to_factorial == 0:
return 1
# Calculate factorial iteratively, as it is efficient and avoids recursion depth issues.
factorial_result = 1
for i in range(1, number_to_factorial + 1):
factorial_result *= i
return factorial_resultBig(O) Analysis
Time Complexity
O(n) – The described approach utilizes Catalan numbers to solve the problem. Calculating the nth Catalan number typically involves iterating 'n' times to compute factorials or using dynamic programming. If the problem involves calculating a Catalan number up to n, where n represents the number of branch pairs, this will determine the overall complexity. Since the dominant operation is calculating the nth Catalan number, and this calculation is done linearly with respect to n, the time complexity is O(n).
Space Complexity
O(1) – The provided plain English explanation focuses on computing a Catalan number. While the calculation method isn't explicitly defined, the core idea revolves around applying the Catalan number formula to the given number of branch pairs. Assuming a direct iterative or formulaic approach for Catalan number calculation, only a few variables are needed to store intermediate values and the final result. The space required is therefore independent of the input size N (number of branch pairs). Thus, the auxiliary space complexity is constant.
Edge Cases
| Case | How to Handle |
|---|---|
| n = 0, no branches to close | Return 1 since there is one possibility: closing no branches. |
| restrictions is null or empty | If restrictions is null or empty, return 2^n, as all combinations are valid. |
| n = 1, one branch and any restrictions | If n=1, and there are any restrictions return 1 else if restrictions is null, return 2. |
| restrictions contains duplicate restrictions (e.g., [1, 2] and [1, 2]) | The bitmask approach should handle duplicates correctly as they only need to be checked once. |
| restrictions contains invalid branch numbers (e.g., x > n or x <= 0) | Validate the restriction input to ensure that all values within are within the range [1,n]; otherwise, return error. |
| Large n exceeding the maximum integer size | Using bit manipulation, n should be limited to a reasonable size like n <=30 to avoid integer overflow issues when calculating 2^n, so return an error if the value is too large. |
| Restrictions create a cycle (e.g., [1,2], [2,3], [3,1]) | The bitmask approach inherently handles cycles correctly, as it iterates through all valid combinations regardless of cycle existence. |
| n is a very large number leading to exponential time complexity and a potential timeout. | The algorithm has exponential time complexity, so ensure that the input n is not too large to avoid a timeout, possibly up to 20 to 30. |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
