Number of Ways to Divide a Long Corridor

Hard

Asked by:

3 views

Topics:

ArraysStringsGreedy Algorithms

Along a long library corridor, there is a line of seats and decorative plants. You are given a 0-indexed string corridor of length n consisting of letters 'S' and 'P' where each 'S' represents a seat and each 'P' represents a plant.

One room divider has already been installed to the left of index 0, and another to the right of index n - 1. Additional room dividers can be installed. For each position between indices i - 1 and i (1 <= i <= n - 1), at most one divider can be installed.

Divide the corridor into non-overlapping sections, where each section has exactly two seats with any number of plants. There may be multiple ways to perform the division. Two ways are different if there is a position with a room divider installed in the first way but not in the second way.

Return the number of ways to divide the corridor. Since the answer may be very large, return it modulo 10⁹ + 7. If there is no way, return 0.

Example 1:

Input: corridor = "SSPPSPS"
Output: 3
Explanation: There are 3 different ways to divide the corridor.
The black bars in the above image indicate the two room dividers already installed.
Note that in each of the ways, each section has exactly two seats.

Example 2:

Input: corridor = "PPSPSP"
Output: 1
Explanation: There is only 1 way to divide the corridor, by not installing any additional dividers.
Installing any would create some section that does not have exactly two seats.

Example 3:

Input: corridor = "S"
Output: 0
Explanation: There is no way to divide the corridor because there will always be a section that does not have exactly two seats.

Constraints:

n == corridor.length
1 <= n <= 10⁵
corridor[i] is either 'S' or 'P'.

Number of Ways to Divide a Long Corridor

Hard

Asked by:

3 views

Topics:

ArraysStringsGreedy Algorithms

Along a long library corridor, there is a line of seats and decorative plants. You are given a 0-indexed string corridor of length n consisting of letters 'S' and 'P' where each 'S' represents a seat and each 'P' represents a plant.

One room divider has already been installed to the left of index 0, and another to the right of index n - 1. Additional room dividers can be installed. For each position between indices i - 1 and i (1 <= i <= n - 1), at most one divider can be installed.

Divide the corridor into non-overlapping sections, where each section has exactly two seats with any number of plants. There may be multiple ways to perform the division. Two ways are different if there is a position with a room divider installed in the first way but not in the second way.

Return the number of ways to divide the corridor. Since the answer may be very large, return it modulo 10⁹ + 7. If there is no way, return 0.

Example 1:

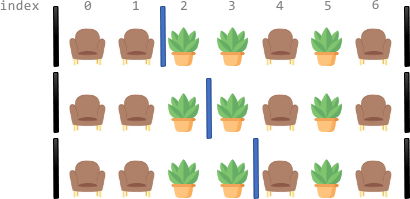
Input: corridor = "SSPPSPS"
Output: 3
Explanation: There are 3 different ways to divide the corridor.
The black bars in the above image indicate the two room dividers already installed.
Note that in each of the ways, each section has exactly two seats.

Example 2:

Input: corridor = "PPSPSP"
Output: 1
Explanation: There is only 1 way to divide the corridor, by not installing any additional dividers.
Installing any would create some section that does not have exactly two seats.

Example 3:

Input: corridor = "S"
Output: 0
Explanation: There is no way to divide the corridor because there will always be a section that does not have exactly two seats.

Constraints:

n == corridor.length
1 <= n <= 10⁵
corridor[i] is either 'S' or 'P'.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the maximum length of the corridor string?
If the number of seats is odd, or less than two, what value should I return?
Can the input string be null or empty?
Are the seats and plants guaranteed to be represented only by 'S' and 'P' characters, respectively?
If no valid division is possible (e.g., not enough seats or no plants between seat pairs to divide), should I return 0, or is there a specific error code or exception I should raise?

Brute Force Solution

Approach

The brute force method for dividing a corridor into sections involves trying every possible arrangement of dividers. We essentially explore all combinations, checking if each combination is valid according to the problem's rules. If it is a valid configuration, we increment a counter, allowing us to exhaustively count all valid divisions.

Here's how the algorithm would work step-by-step:

Consider placing dividers at every possible location within the corridor.
For each possible arrangement of dividers, check if the resulting sections meet the problem's specific criteria (for example, checking if each section contains exactly two plants or if any sections have fewer than two plants).
If a particular arrangement of dividers is valid according to the problem's constraints, mark it as a successful division.
Keep a running count of all the successful, valid divisions you encounter while trying out all possible arrangements.
Once you've exhaustively explored every single possibility of divider placements, the final count represents the total number of valid ways to divide the corridor.

Code Implementation

def number_of_ways_to_divide_a_long_corridor_brute_force(corridor):
    number_of_valid_ways = 0
    number_of_positions = len(corridor)

    # Iterate through all possible divider combinations
    for i in range(1 << (number_of_positions - 1)):
        divider_positions = []
        for j in range(number_of_positions - 1):
            if (i >> j) & 1:
                divider_positions.append(j + 1)

        sections = []
        start = 0
        for divider_position in divider_positions:
            sections.append(corridor[start:divider_position])
            start = divider_position
        sections.append(corridor[start:])

        is_valid = True
        for section in sections:
            plant_count = section.count('P')
            # Section needs exactly two plants
            if plant_count != 2 and plant_count != 0:
                is_valid = False
                break

        if is_valid:
            plant_count_total = corridor.count('P')
            if plant_count_total % 2 == 0 and plant_count_total > 0:
              number_of_valid_ways += 1
    return number_of_valid_ways

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(2^n) – The brute force method considers every possible placement of dividers. For a corridor of length n, there are n-1 potential locations to place a divider. At each location, we either place a divider or we don't. This leads to 2^(n-1) possible combinations of divider placements. Since 2^(n-1) is still exponential we can approximate this as 2^n. Each combination needs to be validated against problem constraints. Therefore, the time complexity is O(2^n).

Space Complexity

O(1) – The brute force approach described involves trying every possible arrangement of dividers. It does not mention using any auxiliary data structures such as arrays, lists, or hash maps to store intermediate results or track visited states. The algorithm only seems to require a counter to keep track of the number of successful divisions. Therefore, the auxiliary space used remains constant regardless of the corridor's length (N), implying O(1) space complexity.

Optimal Solution

Approach

The problem asks for the number of ways to divide a corridor into sections, ensuring each section contains exactly two seats. Instead of exploring every possible combination of divisions, we focus only on the crucial 'seat' positions. The optimal approach involves identifying seat pairs and then calculating the product of the spaces between these pairs.

Here's how the algorithm would work step-by-step:

First, count the number of seats in the corridor. If the number of seats is odd, there are zero ways to divide the corridor because each section needs exactly two seats.
If the number of seats is even, find the positions of all the seats in the corridor, ignoring the plants.
Consider the first two seats. The section divider can only be placed *after* the second seat. We can’t divide the corridor before that.
Now, consider the second pair of seats. Count the number of plants between the second and third seat. This count + 1 gives the number of places to divide the corridor between the first and second pair.
Repeat the process for all consecutive pairs of seats. Count the plants + 1 between each pair.
Multiply all the 'plants + 1' values that you have calculated to find the total number of ways to divide the corridor. If there's only one pair of seats, the answer is simply 1 since there's no choice to be made where to divide.

Code Implementation

def number_of_ways_to_divide(corridor):
    seat_positions = []
    for i, element in enumerate(corridor):
        if element == 'S':
            seat_positions.append(i)

    number_of_seats = len(seat_positions)

    if number_of_seats % 2 != 0:
        return 0

    if number_of_seats == 0:
        return 1

    number_of_ways = 1
    mod = 10**9 + 7
    # Need to calculate the product of plants + 1 between seat pairs.
    for i in range(1, number_of_seats // 2):
        first_seat_index = seat_positions[2 * i - 1]
        second_seat_index = seat_positions[2 * i]
        plants_between_seats = second_seat_index - first_seat_index - 1
        number_of_ways = (number_of_ways * (plants_between_seats + 1)) % mod

    # If there is only one pair, there's only one possible division.
    if number_of_seats == 2:
        return 1

    return number_of_ways

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through the corridor string once to count the seats and store their positions. After that, it iterates through the list of seat positions (which has a maximum size of n, where n is the length of the corridor) to calculate the spaces between the seat pairs. Since both iterations depend on the length of the corridor, the time complexity is linear, O(n).

Space Complexity

O(N) – The algorithm identifies and stores the positions of all seats in the corridor. This requires an auxiliary list or array to hold these seat indices. The size of this list is directly proportional to the number of seats, which, in the worst case, could be proportional to the length of the corridor, N. Therefore, the space complexity is O(N).

Edge Cases

Case	How to Handle
Null or empty input string	Return 0, as there are no corridors to divide.
String with length 1	Return 0, as there aren't enough plants and seats to form a section.
String with no seats	Return 0, as no division is possible without seats.
String with only one seat	Return 0, as an even number of seats is required.
String with an odd number of seats	Return 0, as each section must have exactly two seats, requiring an even total.
String with only plants	Return 0, as there are no seats to form sections.
String starts or ends with a seat but contains only two seats total	Return 1 because the whole corridor forms one valid section.
Large input string to test performance	Ensure the algorithm has a time complexity suitable for large inputs, e.g., O(n) where n is the length of the corridor string.