Partition Array Into Two Arrays to Minimize Sum Difference
HardYou are given an integer array nums of 2 * n integers. You need to partition nums into two arrays of length n to minimize the absolute difference of the sums of the arrays. To partition nums, put each element of nums into one of the two arrays.
Return the minimum possible absolute difference.
Example 1:
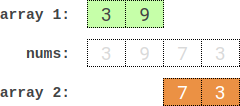
Input: nums = [3,9,7,3] Output: 2 Explanation: One optimal partition is: [3,9] and [7,3]. The absolute difference between the sums of the arrays is abs((3 + 9) - (7 + 3)) = 2.
Example 2:
Input: nums = [-36,36] Output: 72 Explanation: One optimal partition is: [-36] and [36]. The absolute difference between the sums of the arrays is abs((-36) - (36)) = 72.
Example 3:
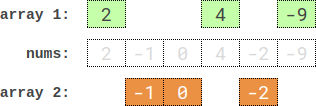
Input: nums = [2,-1,0,4,-2,-9] Output: 0 Explanation: One optimal partition is: [2,4,-9] and [-1,0,-2]. The absolute difference between the sums of the arrays is abs((2 + 4 + -9) - (-1 + 0 + -2)) = 0.
Constraints:
1 <= n <= 15nums.length == 2 * n-107 <= nums[i] <= 107
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the size of the input array `nums` and the range of integer values within it?
- Can the input array `nums` contain negative numbers, zeros, or duplicate values?
- Is it guaranteed that the input array `nums` will always have an even length and be non-empty?
- If multiple partitions result in the same minimum sum difference, does it matter which one is chosen?
- What should be returned if the input array is empty or has an odd length (although the problem statement says even length, it's good to confirm expected behavior for invalid inputs)?
Brute Force Solution
Approach
We want to divide a collection of numbers into two groups so that the sum of numbers in each group is as close as possible. The brute force way to do this is to consider every single possible way to split the original collection into two parts and then see which split results in the smallest difference between the two group sums.
Here's how the algorithm would work step-by-step:
- Think about each number in the original collection.
- For every number, decide if it will go into the first group or the second group.
- Go through all the possible combinations of assigning each number to one of the two groups.
- For each combination, calculate the total sum for the first group and the total sum for the second group.
- Find the difference between these two sums.
- Keep track of the smallest difference you've found so far.
- After trying every single possible assignment for every number, the smallest difference you recorded is your answer.
Code Implementation
def partition_array_minimize_sum_difference_brute_force(original_numbers):
number_of_elements = len(original_numbers)
smallest_difference_found = float('inf')
# Iterate through all possible combinations of assigning elements to two groups
for i in range(1 << number_of_elements):
first_group_sum = 0
second_group_sum = 0
# Determine which group each number belongs to based on the bitmask
for bit_position in range(number_of_elements):
if (i >> bit_position) & 1:
first_group_sum += original_numbers[bit_position]
else:
second_group_sum += original_numbers[bit_position]
# Calculate the absolute difference between the two group sums
current_difference = abs(first_group_sum - second_group_sum)
# Update the smallest difference if the current one is smaller
smallest_difference_found = min(smallest_difference_found, current_difference)
# This smallest difference represents the minimum achievable sum difference
return smallest_difference_foundBig(O) Analysis
Optimal Solution
Approach
This problem involves splitting a collection of numbers into two groups so their sums are as close as possible. The key insight is to realize that finding the perfect split is equivalent to finding a subset of numbers that sums up to exactly half of the total sum, or as close to it as possible. We can then efficiently find this sum by exploring combinations.
Here's how the algorithm would work step-by-step:
- First, calculate the total sum of all the numbers.
- Our goal is to create two groups whose sums are as close as possible, meaning each group should ideally have a sum around half of the total sum.
- Think about this as trying to find a subset of the original numbers that adds up to exactly half of the total sum, or the largest sum less than or equal to half the total sum that we can form.
- We can systematically explore all possible combinations of numbers that can form a subset, keeping track of all the different sums we can achieve using these subsets.
- Once we have all the achievable subset sums, we look for the one that is closest to, but not exceeding, half of the total sum.
- If we find a subset that sums up to exactly half of the total sum, then the remaining numbers will automatically form the other group, and their sum will also be half the total, giving us a perfect split.
- If we can't find a subset that sums up to exactly half, we choose the largest achievable subset sum that is less than half the total. The difference between the total sum and twice this chosen subset sum will be the minimum possible difference between the two groups.
- This approach avoids trying every single way to split the numbers into two groups by focusing on finding a specific target sum for one of the groups.
Code Implementation
def minimum_difference(array_of_numbers):
total_sum_of_elements = sum(array_of_numbers)
target_sum_for_one_half = total_sum_of_elements // 2
# Keep track of all achievable subset sums.
achievable_sums = {0}
for current_number in array_of_numbers:
new_sums_to_add = set()
for existing_sum in achievable_sums:
new_sum = existing_sum + current_number
new_sums_to_add.add(new_sum)
achievable_sums.update(new_sums_to_add)
# Find the largest achievable sum that is less than or equal to the target half sum.
closest_sum_to_half = 0
for subset_sum in achievable_sums:
if subset_sum <= target_sum_for_one_half:
closest_sum_to_half = max(closest_sum_to_half, subset_sum)
# The minimum difference is the total sum minus twice the closest sum found.
return total_sum_of_elements - 2 * closest_sum_to_halfBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Input array is null or empty | The problem statement implies an array of even length, so null or empty inputs should ideally be validated upfront to prevent runtime errors. |
| Input array has odd length | The problem statement guarantees an even length array; if this constraint is violated, the partitioning into equal halves is impossible. |
| Input array contains only two elements | This is the smallest valid input, and the solution should correctly partition these two elements into two arrays of length one. |
| All elements in the input array are identical | Regardless of the value, if all elements are the same, any partition will result in a sum difference of zero, which the algorithm should find. |
| Input array contains negative numbers | The algorithm should handle negative numbers correctly in sum calculations, as the goal is the absolute difference. |
| Input array contains zeros | Zeros do not affect the sum difference, and the algorithm should integrate them into partitions without special handling. |
| Large input array size (e.g., 2N elements where N is large) | The chosen algorithm's time complexity must be efficient enough to handle large inputs without exceeding typical time limits. |
| Integer overflow during sum calculation | Using a data type that can accommodate the maximum possible sum of elements is crucial to prevent overflow errors. |