Pascal's Triangle #12 Most Asked
EasyGiven an integer numRows, return the first numRows of Pascal's triangle.
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:
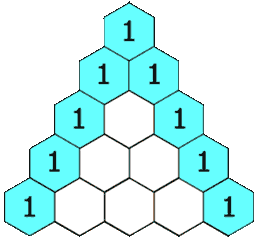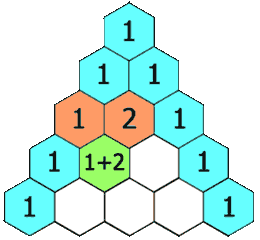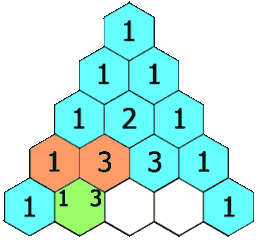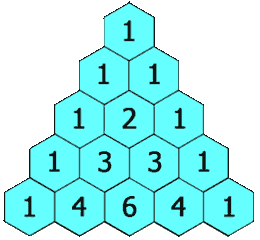
Example 1:
Input: numRows = 5 Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
Example 2:
Input: numRows = 1 Output: [[1]]
Constraints:
1 <= numRows <= 30
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the expected range for `numRows`? Can it be zero or negative?
- Should the returned list of lists contain only integers, or are other data types possible?
- Is there a maximum value for `numRows` that I should be aware of, potentially affecting memory usage?
- Could you provide an example of the expected output format for `numRows = 3` to ensure I understand the structure?
- Are there any specific error conditions I should handle, such as an invalid input type for `numRows`?
Brute Force Solution
Approach
The goal is to build Pascal's Triangle row by row. The brute force method calculates each number in the triangle independently, without reusing previous calculations, based on the definition of Pascal's Triangle.
Here's how the algorithm would work step-by-step:
- To build the triangle, start with the top row, which always contains just the number 1.
- For each subsequent row, figure out each number individually.
- Every number in the triangle is calculated by adding the two numbers directly above it in the previous row. If a number doesn't have two numbers above it (like at the edges), we treat the missing number as zero.
- Repeat the calculation for each number in the current row until the entire row is complete.
- Continue generating rows in this way until we've created the requested number of rows for Pascal's Triangle.
Code Implementation
def generate_pascals_triangle_brute_force(number_of_rows):
pascals_triangle = []
for current_row_index in range(number_of_rows):
current_row = []
for current_column_index in range(current_row_index + 1):
# First and last element of each row is 1
if current_column_index == 0 or current_column_index == current_row_index:
current_row.append(1)
else:
# Calculate the value based on the previous row
previous_row = pascals_triangle[current_row_index - 1]
value = previous_row[current_column_index - 1] + previous_row[current_column_index]
current_row.append(value)
pascals_triangle.append(current_row)
return pascals_triangleBig(O) Analysis
Optimal Solution
Approach
The best way to create Pascal's Triangle is to build it row by row, using the previous row to calculate the next one. Each number in a row is the sum of the two numbers directly above it in the previous row. This approach avoids recalculating values and leverages the inherent structure of the triangle.
Here's how the algorithm would work step-by-step:
- Start with the first row, which contains only the number 1.
- For each subsequent row, the first and last number are always 1.
- For the numbers in between the first and last, calculate their value by adding the two numbers directly above them in the previous row.
- Repeat this process for each row until you reach the desired number of rows.
- Each row you create builds upon the previous row, so you only need to store the previous row to calculate the current one.
Code Implementation
def generate_pascals_triangle(number_of_rows):
pascals_triangle = []
previous_row = []
for row_index in range(number_of_rows):
current_row = []
# The first element of each row is always 1.
current_row.append(1)
# Calculate intermediate values based on the previous row
for element_index in range(1, row_index):
current_element = previous_row[element_index - 1] + previous_row[element_index]
current_row.append(current_element)
# The last element of each row is also always 1.
if row_index > 0:
current_row.append(1)
pascals_triangle.append(current_row)
# Store the current row as previous for the next iteration.
previous_row = current_row
return pascals_triangleBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| numRows is 0 | Return an empty list representing an empty Pascal's triangle. |
| numRows is 1 | Return a list containing a single list with the element 1: [[1]]. |
| numRows is a very large number (e.g., > 30) | The size of the Pascal's triangle grows exponentially, potentially leading to memory issues or integer overflows for large numbers; consider memory optimization or using a language with arbitrary-precision arithmetic. |
| Negative input for numRows | Return an empty list, or throw an IllegalArgumentException since Pascal's triangle is not defined for negative rows. |
| Integer overflow when calculating elements in large rows | Use a data type with a larger range (e.g., long in Java or Python) to avoid integer overflow, or return early if overflow is likely to occur. |
| Memory constraints for very large numRows | If memory is limited, consider generating and returning rows iteratively without storing the entire triangle in memory. |
| Floating point precision issues (though Pascal's Triangle uses integers, hypothetically handling large floating point numbers multiplied for row values) | Since the output must be integers, round the values after multiplication. |
| Check if the given row number exceeds the maximum safe integer allowed by javascript | Return null or an empty list if the row number is bigger than Number.MAX_SAFE_INTEGER. |