Path Existence Queries in a Graph I

Medium

Asked by:

7 views

Topics:

GraphsArraysDynamic Programming

You are given an integer n representing the number of nodes in a graph, labeled from 0 to n - 1.

You are also given an integer array nums of length n sorted in non-decreasing order, and an integer maxDiff.

An undirected edge exists between nodes i and j if the absolute difference between nums[i] and nums[j] is at most maxDiff (i.e., |nums[i] - nums[j]| <= maxDiff).

You are also given a 2D integer array queries. For each queries[i] = [u_i, v_i], determine whether there exists a path between nodes u_i and v_i.

Return a boolean array answer, where answer[i] is true if there exists a path between u_i and v_i in the i^th query and false otherwise.

Example 1:

Input: n = 2, nums = [1,3], maxDiff = 1, queries = [[0,0],[0,1]]

Output: [true,false]

Explanation:

Query [0,0]: Node 0 has a trivial path to itself.
Query [0,1]: There is no edge between Node 0 and Node 1 because |nums[0] - nums[1]| = |1 - 3| = 2, which is greater than maxDiff.
Thus, the final answer after processing all the queries is [true, false].

Example 2:

Input: n = 4, nums = [2,5,6,8], maxDiff = 2, queries = [[0,1],[0,2],[1,3],[2,3]]

Output: [false,false,true,true]

Explanation:

The resulting graph is:

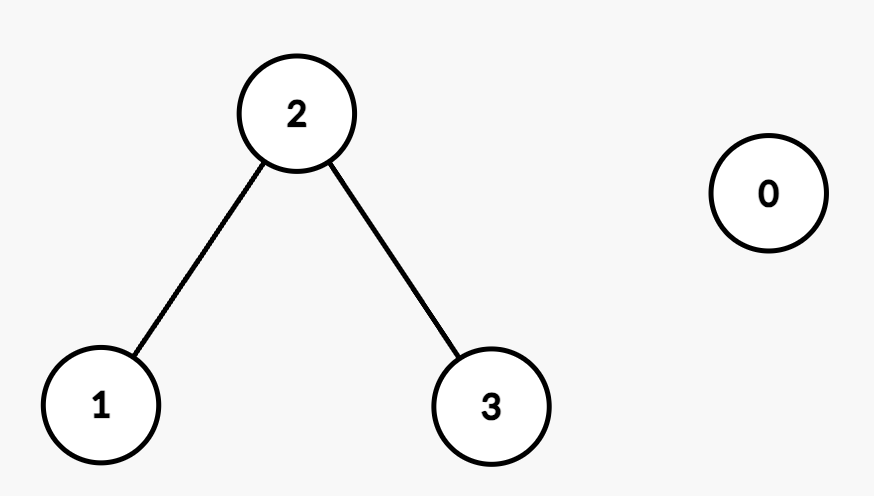
Query [0,1]: There is no edge between Node 0 and Node 1 because |nums[0] - nums[1]| = |2 - 5| = 3, which is greater than maxDiff.
Query [0,2]: There is no edge between Node 0 and Node 2 because |nums[0] - nums[2]| = |2 - 6| = 4, which is greater than maxDiff.
Query [1,3]: There is a path between Node 1 and Node 3 through Node 2 since |nums[1] - nums[2]| = |5 - 6| = 1 and |nums[2] - nums[3]| = |6 - 8| = 2, both of which are within maxDiff.
Query [2,3]: There is an edge between Node 2 and Node 3 because |nums[2] - nums[3]| = |6 - 8| = 2, which is equal to maxDiff.
Thus, the final answer after processing all the queries is [false, false, true, true].

Constraints:

1 <= n == nums.length <= 10⁵
0 <= nums[i] <= 10⁵
nums is sorted in non-decreasing order.
0 <= maxDiff <= 10⁵
1 <= queries.length <= 10⁵
queries[i] == [u_i, v_i]
0 <= u_i, v_i < n

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range of values for the nodes in the graph, and what data type are they?
Is the graph directed or undirected? If directed, can there be cycles?
What are the constraints on the number of nodes and edges in the graph?
If a path doesn't exist between two queried nodes, what should the query return (e.g., false, null, or throw an exception)?
Can there be self-loops or multiple edges between the same two nodes?

Brute Force Solution

Approach

The problem asks us to determine if a path exists between two specific points in a network. The brute force approach explores every single possible route to check for a connection. We'll try out every combination of steps from the start point to the destination.

Here's how the algorithm would work step-by-step:

Start at the initial point.
From that point, explore all directly connected points.
For each of those connected points, explore all the points they are connected to.
Continue exploring outward, level by level, remembering which points you've already visited to avoid going in circles.
For each exploration, if you reach the destination point, then you know a path exists and can stop looking.
If you've explored every possible path from the starting point without finding the destination, then a path does not exist.

Code Implementation

def path_exists_brute_force(number_of_nodes, edges, source_node, destination_node):
    graph = [[] for _ in range(number_of_nodes)]
    for start_node, end_node in edges:
        graph[start_node].append(end_node)

    visited_nodes = [False] * number_of_nodes
    queue = [source_node]
    visited_nodes[source_node] = True

    # Use a queue for breadth-first search to explore all possible paths
    while queue:
        current_node = queue.pop(0)
        if current_node == destination_node:
            return True

        # Explore all neighbors of the current node
        for neighbor_node in graph[current_node]:
            # Avoid revisiting nodes to prevent infinite loops
            if not visited_nodes[neighbor_node]:

                queue.append(neighbor_node)

                visited_nodes[neighbor_node] = True

    # If the queue is empty and the destination isn't found, no path exists
    return False

Big(O) Analysis

Time Complexity

O(n + m) – The algorithm performs a Breadth-First Search (BFS) or Depth-First Search (DFS) on a graph. In the worst case, it visits every node (n) and every edge (m) in the graph to determine if a path exists. Therefore, the time complexity is proportional to the sum of the number of nodes and edges, represented as O(n + m), where n is the number of nodes and m is the number of edges.

Space Complexity

O(N) – The provided solution, based on the plain English description, uses a breadth-first search (BFS) approach. It maintains a queue (implicitly described as 'exploring all directly connected points') and a set to keep track of visited nodes ('remembering which points you've already visited'). In the worst-case scenario, the queue could contain all nodes in the graph, and the visited set could also store all N nodes, where N is the number of nodes in the graph. Therefore, the auxiliary space used is proportional to N, giving a space complexity of O(N).

Optimal Solution

Approach

To efficiently determine if a path exists between nodes in a graph for multiple queries, we preprocess the graph to store connectivity information. This allows us to answer each query in constant time by simply checking a precomputed result, avoiding repeated traversals of the graph for each query.

Here's how the algorithm would work step-by-step:

First, process the graph to identify connected components. Imagine grouping all nodes that can reach each other into separate islands.
For each node, determine which island it belongs to. We are labeling each node based on its connectivity.
Store these island labels for each node in a way that's quick to look up later.
When a query asks if there's a path between two nodes, simply check if they belong to the same island. If they do, a path exists; otherwise, it doesn't.

Code Implementation

def path_exists(number_of_nodes: int, edges: list[list[int]], queries: list[list[int]]) -> list[bool]:
    parent_node = list(range(number_of_nodes))

    def find_connected_component(node_a: int) -> int:
        if parent_node[node_a] != node_a:
            parent_node[node_a] = find_connected_component(parent_node[node_a])
        return parent_node[node_a]

    def union_connected_components(node_a: int, node_b: int) -> None:
        root_a = find_connected_component(node_a)
        root_b = find_connected_component(node_b)
        parent_node[root_a] = root_b

    # Connect nodes based on the given edges.
    for node_a, node_b in edges:
        union_connected_components(node_a, node_b)

    # Ensure the parent array reflects the ultimate parents.
    for node in range(number_of_nodes):
        find_connected_component(node)

    result_list = []
    # Evaluate path existence for each query.
    for start_node, end_node in queries:
        # Check if nodes are in the same connected component.
        result_list.append(parent_node[start_node] == parent_node[end_node])

    return result_list

Big(O) Analysis

Time Complexity

O(n + q) – The algorithm first identifies connected components in the graph, which can be done using Depth First Search (DFS) or Breadth First Search (BFS). The time complexity for this step is O(n), where n represents the number of nodes (and edges, assuming a sparse graph). Then, for each query, we perform a constant-time lookup to check if two nodes belong to the same connected component. If we have q queries, the time complexity for this part is O(q). Therefore, the overall time complexity is O(n + q), where n is the number of nodes in the graph and q is the number of queries.

Space Complexity

O(N) – The algorithm uses an auxiliary data structure to store the island label for each node. This requires a data structure, such as an array or hash map, that can hold a label for each of the N nodes in the graph, where N is the number of nodes. The space used to store the connected component (island) labels grows linearly with the number of nodes in the graph. Therefore, the auxiliary space complexity is O(N).

Edge Cases

Case	How to Handle
Null or empty graph (n=0, edge list empty)	Return an empty list of boolean results since no paths can exist in an empty graph.
Graph with a single node (n=1)	Return a list of 'false' values corresponding to queries that do not originate from that single node.
Queries with identical start and end nodes	Return 'true' if the node exists, 'false' otherwise, as a node is trivially reachable from itself.
Disconnected graph - no path exists between certain nodes.	The pathfinding algorithm (BFS/DFS) should correctly identify and return 'false' for these unreachable queries.
Graph contains cycles	The chosen pathfinding algorithm (BFS or DFS with visited set) handles cycles correctly by avoiding infinite loops and revisiting nodes.
Large graph and large number of queries (scalability)	Consider using a more efficient pathfinding algorithm like BFS and avoid repeatedly constructing the graph adjacency list for each query; consider pre-computing path information if memory allows.
All queries ask for the same path	The algorithm should correctly handle repeated queries without performance degradation, potentially benefiting from caching results if implemented.
Graph represented with self-loops (edge from a node to itself)	The pathfinding algorithm should not get stuck in a self-loop, but recognize it as a valid (trivial) path from a node to itself if the query asks for it.

Null or empty graph (n=0, edge list empty)

How to Handle:

Return an empty list of boolean results since no paths can exist in an empty graph.

Graph with a single node (n=1)

How to Handle:

Return a list of 'false' values corresponding to queries that do not originate from that single node.

Queries with identical start and end nodes

How to Handle:

Return 'true' if the node exists, 'false' otherwise, as a node is trivially reachable from itself.

Disconnected graph - no path exists between certain nodes.

How to Handle:

The pathfinding algorithm (BFS/DFS) should correctly identify and return 'false' for these unreachable queries.

Graph contains cycles

How to Handle:

The chosen pathfinding algorithm (BFS or DFS with visited set) handles cycles correctly by avoiding infinite loops and revisiting nodes.

Large graph and large number of queries (scalability)

How to Handle:

Consider using a more efficient pathfinding algorithm like BFS and avoid repeatedly constructing the graph adjacency list for each query; consider pre-computing path information if memory allows.

All queries ask for the same path

How to Handle:

The algorithm should correctly handle repeated queries without performance degradation, potentially benefiting from caching results if implemented.

Graph represented with self-loops (edge from a node to itself)

How to Handle:

The pathfinding algorithm should not get stuck in a self-loop, but recognize it as a valid (trivial) path from a node to itself if the query asks for it.