Path Sum III #11 Most Asked
MediumGiven the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.
The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).
Example 1:
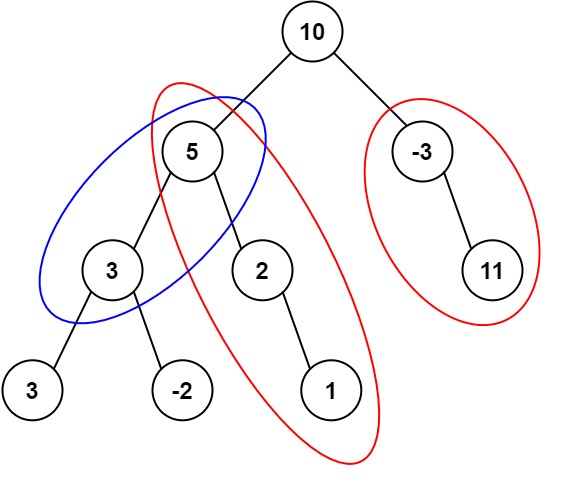
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 Output: 3 Explanation: The paths that sum to 8 are shown.
Example 2:
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 Output: 3
Constraints:
- The number of nodes in the tree is in the range
[0, 1000]. -109 <= Node.val <= 109-1000 <= targetSum <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the node values in the binary tree and the targetSum? Can they be negative, zero, or only positive?
- Are there any constraints on the number of nodes in the tree, such as a maximum height or total node count?
- If there are no paths that sum to the targetSum, should I return 0?
- When you say 'downwards', is it strictly parent to immediate child, or can we skip levels as long as the path follows a downward direction?
- Are the node values integers, or could they be floating-point numbers?
Brute Force Solution
Approach
The brute force approach involves exploring every single path in the tree to see if it sums up to the target value. We essentially check all possible starting points and then try all possible paths downwards from those points. This ensures no possible combination is missed, guaranteeing we find all valid paths, even if inefficiently.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, the root.
- Check if the value of just this single node equals the target value. If so, we found a path.
- Now, explore all paths starting at the root by going down to the left child.
- For each left child, check if its value alone matches the target. Also check if the path from the root to this left child sums to the target.
- Repeat this process by exploring all paths from the left child down the tree.
- Go back to the root and now explore all paths starting by going down to the right child. Perform the same checks as with the left child.
- Keep repeating this process for every single node in the entire tree. For each node, consider it as the starting point of a potential path and explore all downward paths from that node.
- Count up how many paths you found that matched the target value and that's your answer.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def path_sum_brute_force(root, target_sum):
number_of_paths = 0
def path_sum_from_node(node, current_sum):
nonlocal number_of_paths
if not node:
return
# Check if the current node's value equals the target
if node.val == current_sum:
number_of_paths += 1
# Explore the left and right subtrees
path_sum_from_node(node.left, current_sum - node.val)
path_sum_from_node(node.right, current_sum - node.val)
def traverse_tree(node):
nonlocal number_of_paths
if not node:
return
# Consider each node as a potential starting point
path_sum_from_node(node, target_sum)
# Recursively check subtrees
traverse_tree(node.left)
traverse_tree(node.right)
# Start traversal from the root
traverse_tree(root)
return number_of_pathsBig(O) Analysis
Optimal Solution
Approach
The efficient approach to this tree problem involves clever use of previous information to avoid redundant calculations. It uses a 'prefix sum' strategy combined with a data structure to remember past sums, allowing us to quickly identify paths that meet the target sum.
Here's how the algorithm would work step-by-step:
- Start at the root of the tree and perform a depth-first traversal, going down each branch.
- Keep track of the running sum of node values as you go down each path from the root.
- For each node, check how many paths exist that *end* at that node and add up to the target sum. Do this by calculating the difference between the current running sum and the target sum. Then, check if this difference exists as a previous running sum on the path from the root to the current node.
- Store the frequency of each running sum we encounter in a special tracker as we traverse deeper into the tree. This allows us to efficiently check if a specific difference (needed to reach the target sum) was seen before.
- After processing each node, backtrack by removing the current running sum from the tracker to maintain correct counts for subsequent nodes. This ensures each path's sum is calculated correctly as we explore other parts of the tree.
- The final result is the total count of paths that sum to the target value, found by efficiently identifying and tracking relevant running sums along each branch of the tree.
Code Implementation
def pathSum(root, targetSum): def traverseTree(node, currentSum, prefixSums, pathCount): if not node: return pathCount currentSum += node.val
# Check if there's a path ending at the current node with the target sum
difference = currentSum - targetSum
pathCount += prefixSums.get(difference, 0)
# Update the prefix sums count
prefixSums[currentSum] = prefixSums.get(currentSum, 0) + 1
pathCount = traverseTree(node.left, currentSum, prefixSums, pathCount)
pathCount = traverseTree(node.right, currentSum, prefixSums, pathCount)
# Backtrack: remove the current sum from the prefix sums
prefixSums[currentSum] -= 1 return pathCount # Initialize prefix sums with 0 to account for paths starting at root
prefixSums = {0: 1}
return traverseTree(root, 0, prefixSums, 0)Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root | Return 0 immediately as there are no paths in an empty tree. |
| Single node tree where node value equals targetSum | Return 1 as the single node forms a valid path. |
| All node values are zero and targetSum is zero | The number of paths should be counted correctly, considering all possible downward paths. |
| Tree with many negative numbers and a negative targetSum | The solution must correctly handle negative prefixes and target values during path traversal. |
| Tree with a deep and skewed structure (e.g., linked list) | Ensure the recursion depth does not exceed limits and the time complexity remains reasonable (e.g., O(n) space for prefix sums). |
| TargetSum is a very large number potentially leading to integer overflow if node values are large | Use long data type to store running sums to avoid overflow. |
| Tree with extreme boundary node values near max/min integer limits | Ensure the solution handles extreme values correctly without causing unexpected behavior due to integer limits. |
| Multiple valid paths exist summing to the targetSum | The algorithm should count *all* valid paths, not just the first one found. |