Paths in Matrix Whose Sum Is Divisible by K
HardYou are given a 0-indexed m x n integer matrix grid and an integer k. You are currently at position (0, 0) and you want to reach position (m - 1, n - 1) moving only down or right.
Return the number of paths where the sum of the elements on the path is divisible by k. Since the answer may be very large, return it modulo 109 + 7.
Example 1:
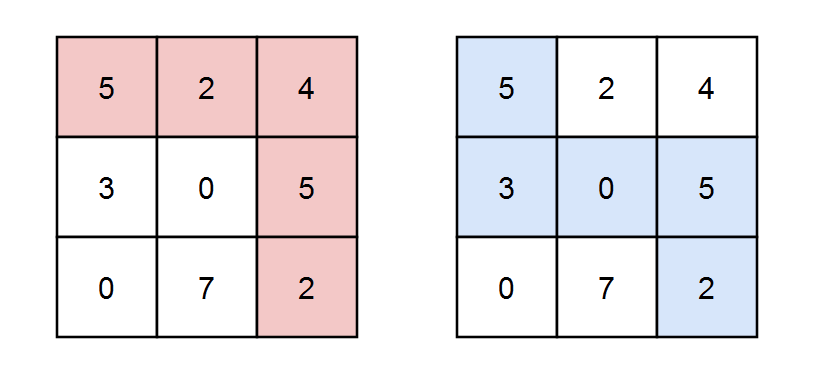
Input: grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3 Output: 2 Explanation: There are two paths where the sum of the elements on the path is divisible by k. The first path highlighted in red has a sum of 5 + 2 + 4 + 5 + 2 = 18 which is divisible by 3. The second path highlighted in blue has a sum of 5 + 3 + 0 + 5 + 2 = 15 which is divisible by 3.
Example 2:

Input: grid = [[0,0]], k = 5 Output: 1 Explanation: The path highlighted in red has a sum of 0 + 0 = 0 which is divisible by 5.
Example 3:
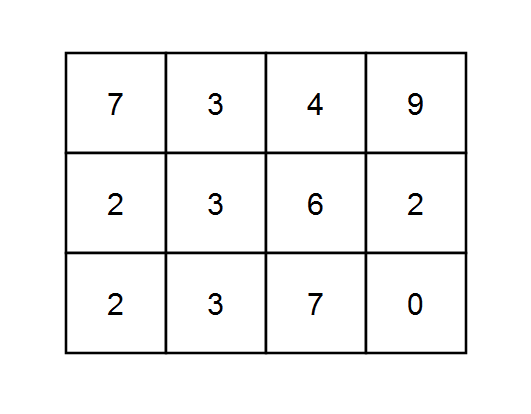
Input: grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1 Output: 10 Explanation: Every integer is divisible by 1 so the sum of the elements on every possible path is divisible by k.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 5 * 1041 <= m * n <= 5 * 1040 <= grid[i][j] <= 1001 <= k <= 50
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the matrix, and what is the maximum size of each dimension?
- Can the values within the matrix be negative, zero, or only positive integers?
- What should I return if there are no paths whose sum is divisible by K? Should I return the number of paths modulo some number?
- Is K guaranteed to be a positive integer?
- Does the path have to start at the top-left corner and end at the bottom-right corner, and can we only move down or right?
Brute Force Solution
Approach
The brute force strategy involves exploring every single possible path through the matrix. We will walk each possible route from the starting point to the destination and check if the sum of the numbers on that route is divisible by the given number. Since this method will explore every combination it will be time consuming.
Here's how the algorithm would work step-by-step:
- Start at the top-left corner of the matrix.
- At each step, you have two choices: move down or move right.
- Explore every possible path by making all combinations of 'down' and 'right' movements until you reach the bottom-right corner.
- For each path you take, keep a running total of the numbers you encounter along the way.
- Once you reach the bottom-right corner, check if the running total for that path is divisible by the given number.
- If the total is divisible, count that path as a valid path.
- After exploring every possible path, return the total count of valid paths.
Code Implementation
def paths_divisible_by_k_brute_force(matrix, k_value):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
valid_path_count = 0
def explore_paths(row_index, column_index, current_sum):
nonlocal valid_path_count
# Add the current cell's value to the running sum
current_sum += matrix[row_index][column_index]
# Base case: Reached the bottom-right corner
if row_index == number_of_rows - 1 and column_index == number_of_columns - 1:
if current_sum % k_value == 0:
valid_path_count += 1
return
# Explore moving down, if possible
if row_index + 1 < number_of_rows:
# Recur to explore the path going down
explore_paths(row_index + 1, column_index, current_sum)
# Explore moving right, if possible
if column_index + 1 < number_of_columns:
# Recur to explore the path going right
explore_paths(row_index, column_index + 1, current_sum)
# Start exploring paths from the top-left corner
explore_paths(0, 0, 0)
return valid_path_countBig(O) Analysis
Optimal Solution
Approach
The efficient solution involves calculating reachable sums along possible paths in the matrix and checking their divisibility by K. Instead of exploring every possible path, we track the possible sums we can achieve at each position, keeping in mind the remainder when divided by K. This avoids redundant calculations and focuses on the remainders, which are what really matters for divisibility.
Here's how the algorithm would work step-by-step:
- Imagine you are starting at the top-left corner of the matrix.
- As you move through the matrix, you can only go down or right. Each cell has a number.
- Instead of tracking the total sum of a path, keep track of the remainder of the path's sum when divided by K.
- At each cell, calculate the new remainder by adding the cell's value to the previous remainder and taking the result modulo K.
- Store how many different paths result in each possible remainder at each cell.
- When you reach the bottom-right corner, check how many paths have a remainder of 0. These paths have sums divisible by K.
- Use a system to remember the possible remainders at each step so you don't have to recalculate them; like building a small table.
Code Implementation
def paths_divisible_by_k(matrix, k_value):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
# DP table to store remainders and their counts.
dp_table = [[{} for _ in range(number_of_columns)] for _ in range(number_of_rows)]
dp_table[0][0][matrix[0][0] % k_value] = 1
for row_index in range(number_of_rows):
for column_index in range(number_of_columns):
if row_index == 0 and column_index == 0:
continue
# Inherit remainders from the cell above.
if row_index > 0:
for previous_remainder, count in dp_table[row_index - 1][column_index].items():
current_remainder = (previous_remainder + matrix[row_index][column_index]) % k_value
if current_remainder not in dp_table[row_index][column_index]:
dp_table[row_index][column_index][current_remainder] = 0
dp_table[row_index][column_index][current_remainder] += count
# Inherit remainders from the cell to the left.
if column_index > 0:
for previous_remainder, count in dp_table[row_index][column_index - 1].items():
current_remainder = (previous_remainder + matrix[row_index][column_index]) % k_value
if current_remainder not in dp_table[row_index][column_index]:
dp_table[row_index][column_index][current_remainder] = 0
dp_table[row_index][column_index][current_remainder] += count
# Count paths with sum divisible by K (remainder 0).
if 0 in dp_table[number_of_rows - 1][number_of_columns - 1]:
return dp_table[number_of_rows - 1][number_of_columns - 1][0]
else:
return 0Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return 0 immediately as there are no paths. |
| Matrix with only one cell (1x1) | Return 1 if the single cell value is divisible by K, otherwise return 0. |
| K = 0 | Return 0 immediately to avoid division by zero errors, or handle the scenario where the path sum has to be exactly 0. |
| Matrix containing negative numbers | The modulo operation needs to handle negative remainders correctly, ensuring remainders are within [0, K-1]. |
| Large matrix dimensions (N x M), exceeding memory limits for DP table | Consider using a space-optimized DP approach, perhaps only storing the previous row's results. |
| Large values in the matrix, potential integer overflow when calculating path sums | Use a larger integer data type (e.g., long) to store intermediate path sums to prevent overflow. |
| No path exists that has a sum divisible by K | The DP table's final value at the bottom-right cell for remainder 0 will be 0 in this case, indicating no such path. |
| Maximum integer value for matrix elements | Prevent integer overflow when adding maximum integer element to the path sum by appropriate use of long data type or overflow detection. |