Perfect Rectangle
HardGiven an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).
Return true if all the rectangles together form an exact cover of a rectangular region.
Example 1:

Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]] Output: true Explanation: All 5 rectangles together form an exact cover of a rectangular region.
Example 2:

Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]] Output: false Explanation: Because there is a gap between the two rectangular regions.
Example 3:
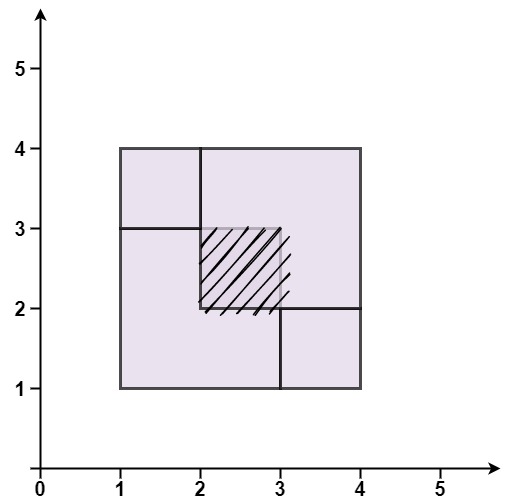
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]] Output: false Explanation: Because two of the rectangles overlap with each other.
Constraints:
1 <= rectangles.length <= 2 * 104rectangles[i].length == 4-105 <= xi < ai <= 105-105 <= yi < bi <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Are the rectangles guaranteed to have positive area, or can a rectangle have a side of length zero?
- Can any of the rectangles overlap each other, and if so, how should overlapping areas be handled?
- Will the input always be valid coordinates representing rectangles, or should I validate that the input coordinates form valid rectangles?
- If a perfect rectangle cannot be formed from the input rectangles, what should the return value be?
- Are the rectangle coordinates provided as integers, or could they be floating-point numbers?
Brute Force Solution
Approach
The brute force approach to the perfect rectangle problem involves considering all possible arrangements of the given smaller rectangles within a larger area. We essentially try placing each rectangle in every possible location and check if it forms a perfect rectangle when combined with the others. This process exhaustively explores all combinations.
Here's how the algorithm would work step-by-step:
- First, find the boundaries of what the final rectangle should look like.
- Imagine covering the space defined by these boundaries with smaller rectangles.
- Start by trying to place the first rectangle in every possible position within this large area.
- For each of those positions of the first rectangle, try placing the second rectangle in every possible position that doesn't overlap the first.
- Continue this process of placing each remaining rectangle, always checking for overlap with previously placed rectangles.
- After placing all rectangles, see if the arrangement perfectly covers the area calculated earlier without any gaps or overlaps.
- If it does, you've found a valid solution! If not, go back and try a different arrangement by moving one of the rectangles, or the starting rectangle and repeat.
Code Implementation
def is_perfect_rectangle_brute_force(rectangles):
min_x = float('inf')
min_y = float('inf')
max_x = float('-inf')
max_y = float('-inf')
area = 0
for rectangle in rectangles:
bottom_left_x = rectangle[0]
bottom_left_y = rectangle[1]
top_right_x = rectangle[2]
top_right_y = rectangle[3]
min_x = min(min_x, bottom_left_x)
min_y = min(min_y, bottom_left_y)
max_x = max(max_x, top_right_x)
max_y = max(max_y, top_right_y)
area += (top_right_x - bottom_left_x) * (top_right_y - bottom_left_y)
expected_area = (max_x - min_x) * (max_y - min_y)
if area != expected_area:
return False
# This part simulates the brute force placement
# by checking if the total area matches the expected area.
occupied_spaces = set()
for rectangle in rectangles:
bottom_left_x = rectangle[0]
bottom_left_y = rectangle[1]
top_right_x = rectangle[2]
top_right_y = rectangle[3]
# Check for overlaps with the brute-force placement
for x in range(bottom_left_x, top_right_x):
for y in range(bottom_left_y, top_right_y):
if (x, y) in occupied_spaces:
return False
occupied_spaces.add((x, y))
# Ensure that every square unit is covered
if len(occupied_spaces) != area:
return False
return TrueBig(O) Analysis
Optimal Solution
Approach
The problem asks if a set of rectangles perfectly covers a larger rectangle without any overlaps or gaps. We can solve this smartly by focusing on area and corners. The core idea is that the sum of the areas of the smaller rectangles must equal the area of the encompassing rectangle, and the corners of the small rectangles define the corners of the larger rectangle.
Here's how the algorithm would work step-by-step:
- Find the coordinates of the bottom-left and top-right corners of what would be the large encompassing rectangle. This is done by looking at all rectangle corners and identifying the smallest and largest x and y values.
- Calculate the area of the potential large encompassing rectangle, using the corner coordinates we just found.
- Calculate the sum of the areas of all the smaller rectangles.
- Check if the total area of smaller rectangles equals the area of the large encompassing rectangle. If they are not equal, there are either gaps or overlaps, and it's impossible.
- Record all the corners of all the small rectangles as points. Use a counting method, like tracking which points appeared an odd number of times.
- The corners of the perfect rectangle (found in step 1) must only appear once in the set of all points. All other points must appear exactly twice because they are edges shared between two rectangles, or four times at the internal corners.
- If all the conditions hold (area equality and corner counts), then the rectangles form a perfect rectangle.
Code Implementation
def is_rectangle_cover(rectangles): if not rectangles:
return True
bottom_left_x = float('inf')
bottom_left_y = float('inf')
top_right_x = float('-inf')
top_right_y = float('-inf')
total_area = 0
corners = {}
for rectangle in rectangles:
x1, y1, x2, y2 = rectangle
bottom_left_x = min(bottom_left_x, x1)
bottom_left_y = min(bottom_left_y, y1)
top_right_x = max(top_right_x, x2)
top_right_y = max(top_right_y, y2)
total_area += (x2 - x1) * (y2 - y1)
# Count occurrences of each corner point
for point in [(x1, y1), (x1, y2), (x2, y1), (x2, y2)]:
corners[point] = corners.get(point, 0) + 1
expected_area = (top_right_x - bottom_left_x) * (top_right_y - bottom_left_y)
# Area of all rectangles must equal area of large rectangle
if total_area != expected_area:
return False
# Check that the 4 corners of the large rectangle appear once.
required_corners = [(bottom_left_x, bottom_left_y),
(bottom_left_x, top_right_y),
(top_right_x, bottom_left_y),
(top_right_x, top_right_y)]
for corner in required_corners:
if corners.get(corner, 0) != 1:
return False
# All other points must appear even number of times.
for corner, count in corners.items():
if corner not in required_corners and count % 2 != 0:
return False
return TrueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty rectangles array | Return false immediately as a perfect rectangle cannot be formed without any rectangles. |
| Single rectangle input | Return true as a single rectangle is inherently a perfect rectangle. |
| Integer overflow during area calculation | Use long long or BigInteger to store the area to prevent potential overflows, especially when dealing with large coordinates. |
| Overlapping rectangles | Use a set to track all the points of the rectangles, and if any point appears more than once (excluding the corner points of the overall rectangle), the rectangles overlap, so return false. |
| Gaps between rectangles | Verify that the total area of all rectangles equals the area of the bounding rectangle, indicating no gaps. |
| Negative coordinates | The solution should correctly handle negative coordinates when determining the bounding rectangle and area calculations. |
| Rectangles that do not form a perfect rectangle (e.g. a 'cross' shape formed by rectangles) | The point set must contain exactly four points, corresponding to the corners of the bounding rectangle to ensure a perfect rectangle formation. |
| Duplicate rectangles (same coordinates) | Adding duplicate rectangles will cause the sum of areas to be larger than the area of the covering rectangle, returning false. |