Push Dominoes
MediumThere are n dominoes in a line, and we place each domino vertically upright. In the beginning, we simultaneously push some of the dominoes either to the left or to the right.
After each second, each domino that is falling to the left pushes the adjacent domino on the left. Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right.
When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces.
For the purposes of this question, we will consider that a falling domino expends no additional force to a falling or already fallen domino.
You are given a string dominoes representing the initial state where:
dominoes[i] = 'L', if theithdomino has been pushed to the left,dominoes[i] = 'R', if theithdomino has been pushed to the right, anddominoes[i] = '.', if theithdomino has not been pushed.
Return a string representing the final state.
Example 1:
Input: dominoes = "RR.L" Output: "RR.L" Explanation: The first domino expends no additional force on the second domino.
Example 2:
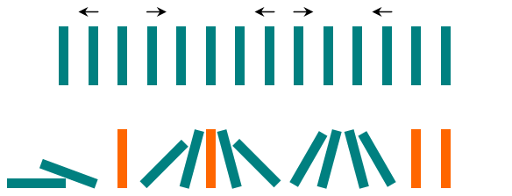
Input: dominoes = ".L.R...LR..L.." Output: "LL.RR.LLRRLL.."
Constraints:
n == dominoes.length1 <= n <= 105dominoes[i]is either'L','R', or'.'.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum length of the dominoes string?
- Can the input string be empty or contain only '.' characters?
- If a domino is pushed from both sides with equal force, but these forces are not 'L' and 'R' (e.g. the ends of the string), what should happen?
- Are the only allowed characters in the input string 'L', 'R', and '.'?
- In cases where there are multiple forces acting on a single domino, should I consider a cumulative force or just the immediate neighboring forces?
Brute Force Solution
Approach
The brute force way to solve the domino problem is to simulate the entire process step by step. We check each domino and how it affects its neighbors at each moment in time, until nothing changes anymore. It's like watching the whole domino effect unfold slowly and carefully.
Here's how the algorithm would work step-by-step:
- Start by looking at each domino individually.
- If a domino is standing, see if its neighbors are pushing it.
- If a domino is pushed from the right, it will fall to the left. If a domino is pushed from the left, it will fall to the right.
- Keep track of which dominoes will fall in the next moment based on these pushes.
- Repeat the process: Update the state of the dominoes based on whether they are falling or still standing.
- Do this over and over again, updating which dominoes are falling based on their neighbors.
- Stop when nothing changes anymore – when all the dominoes have settled into their final positions.
Code Implementation
def push_dominoes_brute_force(dominoes):
dominoes_list = list(dominoes)
size = len(dominoes_list)
while True:
next_dominoes_list = dominoes_list[:]
changed = False
for index in range(size):
if dominoes_list[index] == '.':
left_force = 0
right_force = 0
# Check left neighbor's force.
if index > 0 and dominoes_list[index - 1] == 'R':
right_force = 1
# Check right neighbor's force.
if index < size - 1 and dominoes_list[index + 1] == 'L':
left_force = 1
# Resolve forces and update.
if left_force > right_force:
next_dominoes_list[index] = 'L'
changed = True
elif right_force > left_force:
next_dominoes_list[index] = 'R'
changed = True
dominoes_list = next_dominoes_list
if not changed:
# If no changes were made in the loop, exit.
break
return ''.join(dominoes_list)Big(O) Analysis
Optimal Solution
Approach
The best way to solve this dominoes problem is to figure out how each domino is affected by its neighbors. We can do this by understanding how forces (from the left and right) act on each domino, figuring out which way it will fall, and then building the final arrangement of dominoes.
Here's how the algorithm would work step-by-step:
- First, imagine that each 'R' domino is pushing to the right and each 'L' domino is pushing to the left.
- Then, go through the row of dominoes and figure out the net force on each domino. This means looking at the push from the closest 'R' to the left and the push from the closest 'L' to the right.
- If the force from the left and right is the same, the domino stays standing ('.').
- If the force is stronger from the left ('L'), the domino falls to the left ('L').
- If the force is stronger from the right ('R'), the domino falls to the right ('R').
- By considering the forces acting on each domino, we can determine the final state of each domino without having to simulate the dominoes falling step-by-step.
Code Implementation
def push_dominoes(dominoes: str) -> str:
dominoes_list = list(dominoes)
number_of_dominoes = len(dominoes)
forces = [0] * number_of_dominoes
# Calculate forces from the left
force_from_left = 0
for i in range(number_of_dominoes):
if dominoes_list[i] == 'R':
force_from_left = number_of_dominoes
elif dominoes_list[i] == 'L':
force_from_left = 0
else:
force_from_left = max(force_from_left - 1, 0)
forces[i] += force_from_left
# Calculate forces from the right
force_from_right = 0
for i in range(number_of_dominoes - 1, -1, -1):
if dominoes_list[i] == 'L':
force_from_right = number_of_dominoes
elif dominoes_list[i] == 'R':
force_from_right = 0
else:
force_from_right = max(force_from_right - 1, 0)
forces[i] -= force_from_right
# Determine final state based on net force.
for i in range(number_of_dominoes):
if forces[i] > 0:
dominoes_list[i] = 'R'
elif forces[i] < 0:
dominoes_list[i] = 'L'
else:
dominoes_list[i] = '.'
return "".join(dominoes_list)Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty dominoes string | Return an empty string or null if the input dominoes string is null or empty, as there are no dominoes to process. |
| Dominoes string with a single character | Return the original string directly since a single domino will remain in its initial state. |
| Dominoes string with only '.' characters | Return the original string as no forces are applied, and all dominoes remain standing. |
| Dominoes string with all 'L' characters | Return the original string as all dominoes are already pushed to the left. |
| Dominoes string with all 'R' characters | Return the original string as all dominoes are already pushed to the right. |
| Dominoes string with alternating 'L' and 'R' with some '.' | Ensure the force propagation algorithm correctly handles cases where opposing forces meet, leaving dominoes standing. |
| Dominoes string with large size | The solution's space and time complexity must be considered for large inputs, and potentially optimized to avoid exceeding memory or time limits. |
| Dominoes string with consecutive 'R' followed by consecutive 'L' with '.' in between | Check that forces are applied correctly from both sides, and that if the middle ground is even, dominoes fall correctly and in the case of odd number, it remains '.'. |