Range Sum of BST
EasyGiven the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
Example 1:
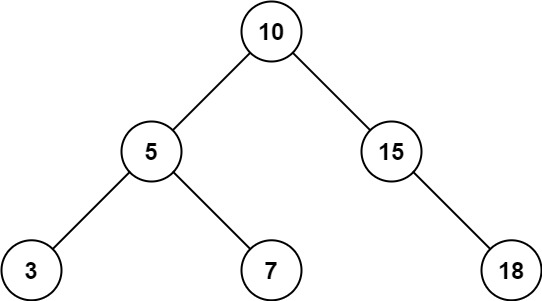
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15 Output: 32 Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.
Example 2:
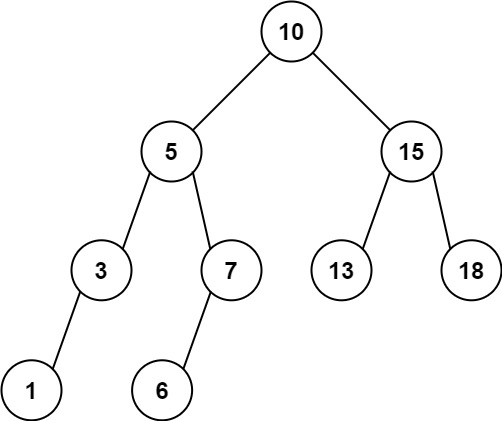
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10 Output: 23 Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.
Constraints:
- The number of nodes in the tree is in the range
[1, 2 * 104]. 1 <= Node.val <= 1051 <= low <= high <= 105- All
Node.valare unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the node values, `low`, and `high`? Are they guaranteed to be integers and positive?
- Is the given tree guaranteed to be a valid Binary Search Tree (BST)?
- What should I return if the tree is empty (root is null)? Should I return 0 in that case?
- Is it possible for `low` to be greater than `high`? If so, how should I handle that case?
- How large can the tree be in terms of the number of nodes?
Brute Force Solution
Approach
The brute force approach to finding the range sum in a Binary Search Tree (BST) involves checking every single node in the tree. We'll visit each node and see if its value falls within our specified range, adding it to a total if it does. This guarantees we don't miss any possible node.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree (the root).
- Check if the value at the current node is within our given range (between the lower and upper bounds).
- If the value is in the range, add it to our running total.
- Now, go down to the left child of the current node and repeat the check from step two.
- After exploring the left side, go down to the right child of the original node and repeat the check from step two there too.
- Keep doing this for every single node in the entire tree, making sure to check if the node exists before attempting to access its value.
- Once you've visited every node in the tree, the running total will represent the sum of all the nodes whose values fell within the specified range.
Code Implementation
def range_sum_bst_brute_force(root, low, high):
total_sum = 0
def inorder_traversal(node):
nonlocal total_sum
if not node:
return
# Recursively visit the left subtree
inorder_traversal(node.left)
# Check if node is within bounds
if low <= node.val <= high:
# Add to total if within bounds
total_sum += node.val
# Recursively visit the right subtree
inorder_traversal(node.right)
inorder_traversal(root)
return total_sumBig(O) Analysis
Optimal Solution
Approach
The clever way to solve this involves carefully navigating the tree, only exploring parts that are actually relevant to our range. We use the special ordering of the tree to avoid unnecessary work, making it super efficient.
Here's how the algorithm would work step-by-step:
- Begin at the very top of the tree.
- If the current number we're looking at is less than the smallest number in our range, we know everything to its left is also too small, so we ignore the left side completely.
- If the current number is larger than the biggest number in our range, we know everything to its right is too big, so we skip the right side.
- If the current number is within our range, we add it to our running total and then explore both the left and right sides because they might also contain numbers within our range.
- Keep doing this, only going down branches that could possibly have relevant numbers.
- Once we've explored all the relevant paths, we have our total sum of numbers within the range.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def range_sum_bst(root, low_range, high_range):
total_sum = 0
def traverse_tree(node):
nonlocal total_sum
if not node:
return
# Skip left subtree if node value is less than the low range.
if node.val < low_range:
traverse_tree(node.right)
# Skip right subtree if node value is greater than the high range.
elif node.val > high_range:
traverse_tree(node.left)
# Node is within range; add to total and explore both subtrees.
else:
total_sum += node.val
traverse_tree(node.left)
traverse_tree(node.right)
traverse_tree(root)
return total_sumBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| root is null | Return 0 immediately, as there are no nodes to sum. |
| low is greater than high | Return 0, as the range is invalid and no nodes can be within it. |
| BST contains only one node and the node's value is within the range [low, high] | Return the node's value directly. |
| BST contains only one node and the node's value is outside the range [low, high] | Return 0. |
| All node values are less than low | Return 0, as no node values fall within the range. |
| All node values are greater than high | Return 0, as no node values fall within the range. |
| Integer overflow when summing node values | Use a larger data type (e.g., long) for the sum to prevent overflow. |
| BST is heavily skewed, resembling a linked list | The algorithm should still function correctly, but the performance will degrade to O(n) as opposed to O(log n) in a balanced BST. |