Range Sum Query 2D - Immutable

Medium

Asked by:

+5

5 views

Topics:

ArraysDynamic Programming

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1:

Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10⁴ <= matrix[i][j] <= 10⁴
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 10⁴ calls will be made to sumRegion.

Range Sum Query 2D - Immutable

Medium

Asked by:

5 views

Topics:

ArraysDynamic Programming

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1:

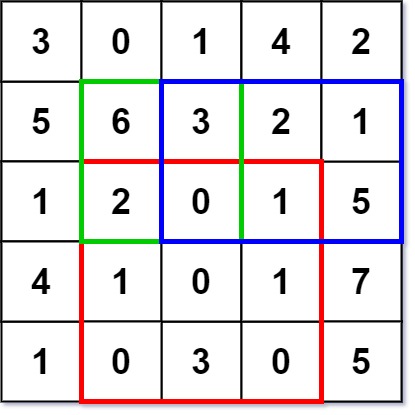
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10⁴ <= matrix[i][j] <= 10⁴
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 10⁴ calls will be made to sumRegion.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the dimensions of the matrix (number of rows and columns)? Are they always positive?
Can the values within the matrix be negative, zero, or only positive?
Are row1, col1, row2, and col2 guaranteed to be within the bounds of the matrix? If not, how should out-of-bounds indices be handled?
Is it possible that row1 > row2 or col1 > col2? If so, what should the sumRegion function return in these cases?
How many times will the sumRegion function be called after the matrix is initialized? Should I optimize for many calls to sumRegion?

Brute Force Solution

Approach

The brute force approach to finding a sum within a rectangle in a grid involves directly calculating the sum for every possible rectangle specified by the user. We achieve this by simply looking at each cell within the given rectangle and adding its value to a running total.

Here's how the algorithm would work step-by-step:

Imagine highlighting the rectangle defined by the top-left and bottom-right corners given to you.
Look at each number that is inside this highlighted rectangle, one by one.
Keep a running sum, starting at zero.
For each number inside the highlighted rectangle, add it to the running sum.
Once you've gone through every number in the rectangle, the running sum will be the answer.

Code Implementation

class NumMatrix:

    def __init__(self, matrix):
        self.matrix = matrix

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        total_sum = 0

        # Iterate through rows within the specified range
        for row_index in range(row1, row2 + 1):

            # Iterate through columns within the specified range
            for column_index in range(col1, col2 + 1):
                # Add the current cell's value to the total sum
                total_sum += self.matrix[row_index][column_index]

        return total_sum

# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n) – The brute force approach iterates through all cells within the specified rectangle in the 2D matrix. Let 'm' be the number of rows and 'n' be the number of columns within the rectangle defined by the query. The algorithm visits each of these m*n cells once to compute the sum. Therefore, the time complexity is directly proportional to the area of the rectangle, resulting in O(m*n).

Space Complexity

O(1) – The described brute force approach only utilizes a running sum variable. This variable consumes a fixed amount of memory regardless of the dimensions of the input matrix. Since no auxiliary data structures that scale with the input size are employed, the auxiliary space complexity is constant.

Optimal Solution

Approach

We can solve this efficiently by pre-calculating sums of rectangles within the larger grid. By storing these pre-calculated sums, we can quickly determine the sum of any rectangular region using only a few simple calculations.

Here's how the algorithm would work step-by-step:

First, create a new grid that will store pre-calculated sums. This grid should be one size larger in both dimensions than the original grid.
Next, fill in this new grid. Each cell will store the sum of all numbers in the original grid from the top-left corner up to that cell's corresponding location. This is done in a way so that each cell's value can be calculated very quickly using the values in the cells above and to the left of it, and the corresponding number in the original grid.
When we need to find the sum of a rectangular region, we use the pre-calculated sums to get the answer very quickly. We take the pre-calculated sum for the bottom-right corner of the desired rectangle, then subtract the sums for the areas above and to the left of it. Finally, we add back the sum of the overlapping region in the top-left to avoid double-subtraction. This gives us the sum of just the numbers within the rectangle we want.

Code Implementation

class NumMatrix:

    def __init__(self, matrix):
        self.matrix = matrix
        if not matrix or not matrix[0]:
            self.sum_grid = [[]]
            return
        number_of_rows = len(matrix)
        number_of_cols = len(matrix[0])
        self.sum_grid = [[0] * (number_of_cols + 1) for _ in range(number_of_rows + 1)]

        # Build the sum grid for fast range queries
        for row_index in range(number_of_rows):
            for col_index in range(number_of_cols):
                self.sum_grid[row_index + 1][col_index + 1] = self.sum_grid[row_index + 1][col_index] + self.sum_grid[row_index][col_index + 1] - self.sum_grid[row_index][col_index] + matrix[row_index][col_index]

    def sumRegion(self, row1, col1, row2, col2):
        # Using precomputed sums for O(1) query
        return self.sum_grid[row2 + 1][col2 + 1] - self.sum_grid[row1][col2 + 1] - self.sum_grid[row2 + 1][col1] + self.sum_grid[row1][col1]

# Your NumMatrix object will be instantiated and called as such:
# numMatrix = NumMatrix(matrix)
# numMatrix.sumRegion(0, 1, 2, 3)
# numMatrix.sumRegion(1, 2, 3, 4)

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n) – The initialization phase involves creating a prefix sum matrix of size (m+1)x(n+1), where m is the number of rows and n is the number of columns in the input matrix. Populating this prefix sum matrix requires iterating through each cell once, performing a constant number of additions. The sumRegion query then performs a fixed number of lookups and arithmetic operations (4 lookups and 3 arithmetic operations) regardless of the dimensions of the region. Therefore, initialization takes O(m*n) time, and the sumRegion queries take O(1) time. Since we're analyzing the complexity of the algorithm as a whole, we focus on the dominant operation, which is creating the prefix sum matrix.

Space Complexity

O(M*N) – The algorithm creates a new grid, which we'll call 'sum_grid', to store pre-calculated sums. The dimensions of this grid are one size larger than the original input matrix in both dimensions, meaning if the input matrix has dimensions M rows and N columns, the 'sum_grid' will have (M+1) rows and (N+1) columns. Therefore, the auxiliary space used by the algorithm is proportional to the number of elements in the 'sum_grid', which is (M+1)*(N+1). This simplifies to O(M*N) since constants are dropped during Big O notation.

Edge Cases

Case	How to Handle
Null or empty matrix input	Return 0 or throw an exception indicating invalid input as there's no matrix to sum.
Zero width or height matrix	Return 0 if the matrix has zero rows or zero columns, signifying an empty matrix.
row1 > row2 or col1 > col2	Return 0 because the specified region is invalid (top-left corner is below/to the right of the bottom-right corner).
row1, col1, row2, or col2 are out of bounds of the matrix	Adjust the coordinates to be within bounds of the matrix or throw an exception indicating an invalid range.
Large matrix dimensions (potential for integer overflow)	Use long data type to store prefix sums to avoid integer overflow during summation.
Matrix with very large positive or negative values	Ensure that intermediate sums do not overflow even with large matrix elements, using long if necessary.
Sum region covering the entire matrix	The prefix sum implementation should handle this case correctly, returning the total sum of all matrix elements.
Multiple calls to sumRegion after preprocessing	The prefix sum data structure should allow for efficient calculation of the sum for any given region after initial construction.