Rank Transform of a Matrix

Hard

Asked by:

25 views

Topics:

ArraysGraphsDynamic Programming

Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

The rank is an integer starting from 1.
If two elements p and q are in the same row or column, then:
- If p < q then rank(p) < rank(q)
- If p == q then rank(p) == rank(q)
- If p > q then rank(p) > rank(q)
The rank should be as small as possible.

The test cases are generated so that answer is unique under the given rules.

Example 1:

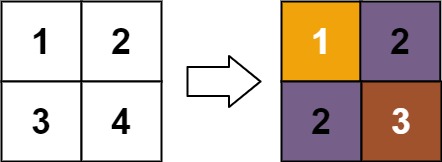
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.

Example 2:

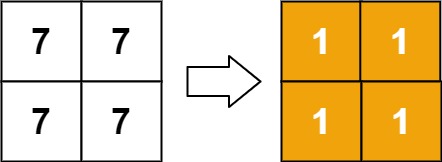
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]

Example 3:

Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 500
-10⁹ <= matrix[row][col] <= 10⁹

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the maximum size of the matrix (number of rows and columns)?
Can the matrix contain negative integers, zero, or floating-point numbers?
If there are multiple elements with the same value in the matrix, how should their ranks be handled?
Is there a specific data structure or format required for the output rank matrix?
What should the rank be if all the elements in a row or column are identical?

Brute Force Solution

Approach

The goal is to assign a rank to each number in a grid based on its value relative to others in its row and column. The brute force approach involves trying every possible rank assignment for each number, making sure it's consistent with all the row and column rules, and then picking the one that works.

Here's how the algorithm would work step-by-step:

Start by trying to assign the smallest possible rank (which is 1) to every number in the grid.
Check if these ranks are correct by comparing each number to all other numbers in its row and column.
If a number is larger than another number in its row or column, make sure its rank is also larger. If it's smaller, its rank should also be smaller. If these rules are broken, the rank assignment is not correct.
If any of the rules are broken, increment the rank of that number by one, and check the rules again.
Repeat this process of incrementing ranks and checking rules until you find a rank assignment where all the rules are satisfied for the entire grid.
Because there may be more than one possible set of rank assignments that could work, keep track of each possible arrangement, until every number in the grid follows the rules relative to the other numbers in its row and column.

Code Implementation

def matrix_rank_transform_brute_force(matrix):
    number_of_rows = len(matrix)
    number_of_columns = len(matrix[0])
    ranks = [[1] * number_of_columns for _ in range(number_of_rows)]

    while True:
        changed = False

        for row_index in range(number_of_rows):
            for column_index in range(number_of_columns):
                current_value = matrix[row_index][column_index]
                current_rank = ranks[row_index][column_index]

                # Check row consistency
                for other_column_index in range(number_of_columns):
                    if other_column_index != column_index:
                        other_value = matrix[row_index][other_column_index]
                        other_rank = ranks[row_index][other_column_index]

                        if current_value > other_value and current_rank <= other_rank:
                            ranks[row_index][column_index] = other_rank + 1
                            changed = True

                        if current_value < other_value and current_rank >= other_rank:
                            ranks[row_index][column_index] = other_rank - 1
                            changed = True

                # Check column consistency
                for other_row_index in range(number_of_rows):
                    if other_row_index != row_index:
                        other_value = matrix[other_row_index][column_index]
                        other_rank = ranks[other_row_index][column_index]

                        if current_value > other_value and current_rank <= other_rank:
                            ranks[row_index][column_index] = other_rank + 1
                            changed = True

                        if current_value < other_value and current_rank >= other_rank:
                            ranks[row_index][column_index] = other_rank - 1
                            changed = True

                if ranks[row_index][column_index] != current_rank:
                    changed = True

        if not changed:
            break

        # Correct ranks must be between 1 and (m * n) (inclusive) to avoid infinite loop.
        for row_index in range(number_of_rows):
            for column_index in range(number_of_columns):
                ranks[row_index][column_index] = max(1, min(number_of_rows * number_of_columns, ranks[row_index][column_index]))

    return ranks

Big(O) Analysis

Time Complexity

O(m*n*m*n*k) – The described brute force approach iterates through each of the m*n elements in the matrix, attempting to assign ranks starting from 1. For each element, it compares its rank with all other elements in its row and column, leading to m+n comparisons in the worst case. If inconsistencies are found, the rank of the current element is incremented, and the comparison process is repeated. The worst case rank that could be assigned to a matrix element is bounded by k, the maximum matrix element value. The time complexity is thus O(m*n*m*n*k), where m and n represent the number of rows and columns in the matrix.

Space Complexity

O(1) – The provided brute force algorithm primarily modifies the input matrix in place and only requires a few variables to iterate through rows and columns and track inconsistencies. It does not create any auxiliary data structures like lists, hashmaps, or recursion stacks whose size scales with the input matrix dimensions (rows and columns). Therefore, the space complexity is dominated by a constant amount of extra memory, irrespective of the size of the input matrix. Hence, the auxiliary space complexity is O(1).

Optimal Solution

Approach

To efficiently assign ranks to elements in a matrix while respecting row and column constraints, we will treat the matrix as a collection of interconnected groups of values and propagate ranks through these groups. We will use a combination of sorting and a clever technique for grouping equal values together to resolve conflicting rank assignments efficiently.

Here's how the algorithm would work step-by-step:

First, we gather all the numbers from the matrix and sort them. This way, we know the order we need to assign ranks.
We start assigning ranks from the smallest number up. For each unique number, we figure out which rows and columns it appears in.
Imagine each row and column as a team. When the same number appears in multiple teams (rows or columns), we want to figure out which team should get what rank, while ensuring the rows and columns respect their internal orders.
For numbers that are the same, but appear in different rows and columns, we use a 'union find' strategy. This is like merging teams together if their members have equal value. This helps us solve conflicting ranks that happen in different rows and columns, effectively grouping equal elements together across rows and columns.
For each group of equal values, we look at the existing ranks in their respective rows and columns. The rank we assign will be one higher than the highest rank currently assigned in any of those rows and columns.
After assigning the rank to the group, we update the ranks in all their associated rows and columns. This ensures ranks correctly propagate through the structure.
Finally, place the calculated ranks back into the matrix, creating the rank-transformed version.

Code Implementation

def rank_transform(matrix):
    rows = len(matrix)
    cols = len(matrix[0]) if rows > 0 else 0

    if rows == 0 or cols == 0:
        return matrix

    numbers_with_positions = []
    for row_index in range(rows):
        for col_index in range(cols):
            numbers_with_positions.append((matrix[row_index][col_index], row_index, col_index))

    numbers_with_positions.sort()

    rank_matrix = [[0] * cols for _ in range(rows)]
    row_ranks = [0] * rows
    col_ranks = [0] * cols

    index = 0
    while index < len(numbers_with_positions):
        start_index = index
        equal_numbers_group = []

        # Group all equal numbers together
        while index < len(numbers_with_positions) and \
              numbers_with_positions[index][0] == numbers_with_positions[start_index][0]:
            equal_numbers_group.append(numbers_with_positions[index])
            index += 1

        # Determine the maximum rank among rows/cols of equal values
        max_rank_for_group = 0
        for _, row_index, col_index in equal_numbers_group:
            max_rank_for_group = max(max_rank_for_group, row_ranks[row_index], col_ranks[col_index])

        # Assign ranks to the equal numbers
        for _, row_index, col_index in equal_numbers_group:
            rank = max_rank_for_group + 1
            rank_matrix[row_index][col_index] = rank

            # Update row and column ranks
            row_ranks[row_index] = rank
            col_ranks[col_index] = rank

    return rank_matrix

Big(O) Analysis

Time Complexity

O(m * n * log(m * n)) – The dominant cost comes from sorting all m * n elements of the matrix initially, which takes O(m * n * log(m * n)) time. Although the union-find operations and rank propagation are conceptually within nested loops iterating through rows and columns for each distinct value, their overall cost is bounded by the initial sorting. Specifically, the grouping and ranking process is performed for each unique value extracted from the sorted list of m * n elements. Therefore the overall time complexity is O(m * n * log(m * n)).

Space Complexity

O(m * n) – The algorithm uses extra space primarily for storing the sorted list of matrix elements, which can have at most m * n elements where m is the number of rows and n is the number of columns. Additionally, the union find data structure, implemented typically as parent arrays, implicitly requires space proportional to the number of rows and columns (m + n). The rank matrix itself (the output) technically contributes to space complexity if not considered in-place, again taking m * n space. Therefore, the dominant space usage comes from the sorted list and output rank matrix, both proportional to m * n, resulting in a space complexity of O(m * n).

Edge Cases

Case	How to Handle
Null or empty matrix	Return an empty matrix (or a matrix of the same dimensions filled with 0s) immediately as there's no input to process.
Matrix with a single row or a single column	The ranking becomes a simple 1D ranking problem which should be handled by the same logic used for the general case.
Matrix with all identical values	All elements should be assigned a rank of 1 in this case; the algorithm should correctly identify and assign this rank.
Matrix with extremely large dimensions (close to memory limits)	Ensure the algorithm uses memory efficiently to avoid out-of-memory errors; consider using generators or iterators where possible to avoid loading the entire matrix into memory at once, or breaking the calculations into chunks.
Matrix with integer overflow potential during calculations (e.g., summing large values)	Use appropriate data types (e.g., `long` in Java or Python's arbitrary-precision integers) to prevent overflow during rank calculations or sorting.
Matrix containing duplicate values that form cycles during rank propagation	The disjoint-set union (DSU) data structure needs to correctly handle cycles, ensuring ranks are consistent within connected components.
Matrix containing negative numbers, zeros, and large positive numbers	The rank transformation algorithm needs to handle the full range of integer values correctly during sorting and rank assignment without errors.
The algorithm exceeds the time limit for large matrices	Optimize the sorting algorithm (use a fast sorting algorithm like mergesort or quicksort with appropriate pivot selection), and ensure efficient implementation of DSU with path compression and union by rank.

Null or empty matrix

How to Handle:

Return an empty matrix (or a matrix of the same dimensions filled with 0s) immediately as there's no input to process.

Matrix with a single row or a single column

How to Handle:

The ranking becomes a simple 1D ranking problem which should be handled by the same logic used for the general case.

Matrix with all identical values

How to Handle:

All elements should be assigned a rank of 1 in this case; the algorithm should correctly identify and assign this rank.

Matrix with extremely large dimensions (close to memory limits)

How to Handle:

Ensure the algorithm uses memory efficiently to avoid out-of-memory errors; consider using generators or iterators where possible to avoid loading the entire matrix into memory at once, or breaking the calculations into chunks.

Matrix with integer overflow potential during calculations (e.g., summing large values)

How to Handle:

Use appropriate data types (e.g., `long` in Java or Python's arbitrary-precision integers) to prevent overflow during rank calculations or sorting.

Matrix containing duplicate values that form cycles during rank propagation

How to Handle:

The disjoint-set union (DSU) data structure needs to correctly handle cycles, ensuring ranks are consistent within connected components.

Matrix containing negative numbers, zeros, and large positive numbers

How to Handle:

The rank transformation algorithm needs to handle the full range of integer values correctly during sorting and rank assignment without errors.

The algorithm exceeds the time limit for large matrices

How to Handle:

Optimize the sorting algorithm (use a fast sorting algorithm like mergesort or quicksort with appropriate pivot selection), and ensure efficient implementation of DSU with path compression and union by rank.