Rectangle Area II #1 Most Asked
HardYou are given a 2D array of axis-aligned rectangles. Each rectangle[i] = [xi1, yi1, xi2, yi2] denotes the ith rectangle where (xi1, yi1) are the coordinates of the bottom-left corner, and (xi2, yi2) are the coordinates of the top-right corner.
Calculate the total area covered by all rectangles in the plane. Any area covered by two or more rectangles should only be counted once.
Return the total area. Since the answer may be too large, return it modulo 109 + 7.
Example 1:
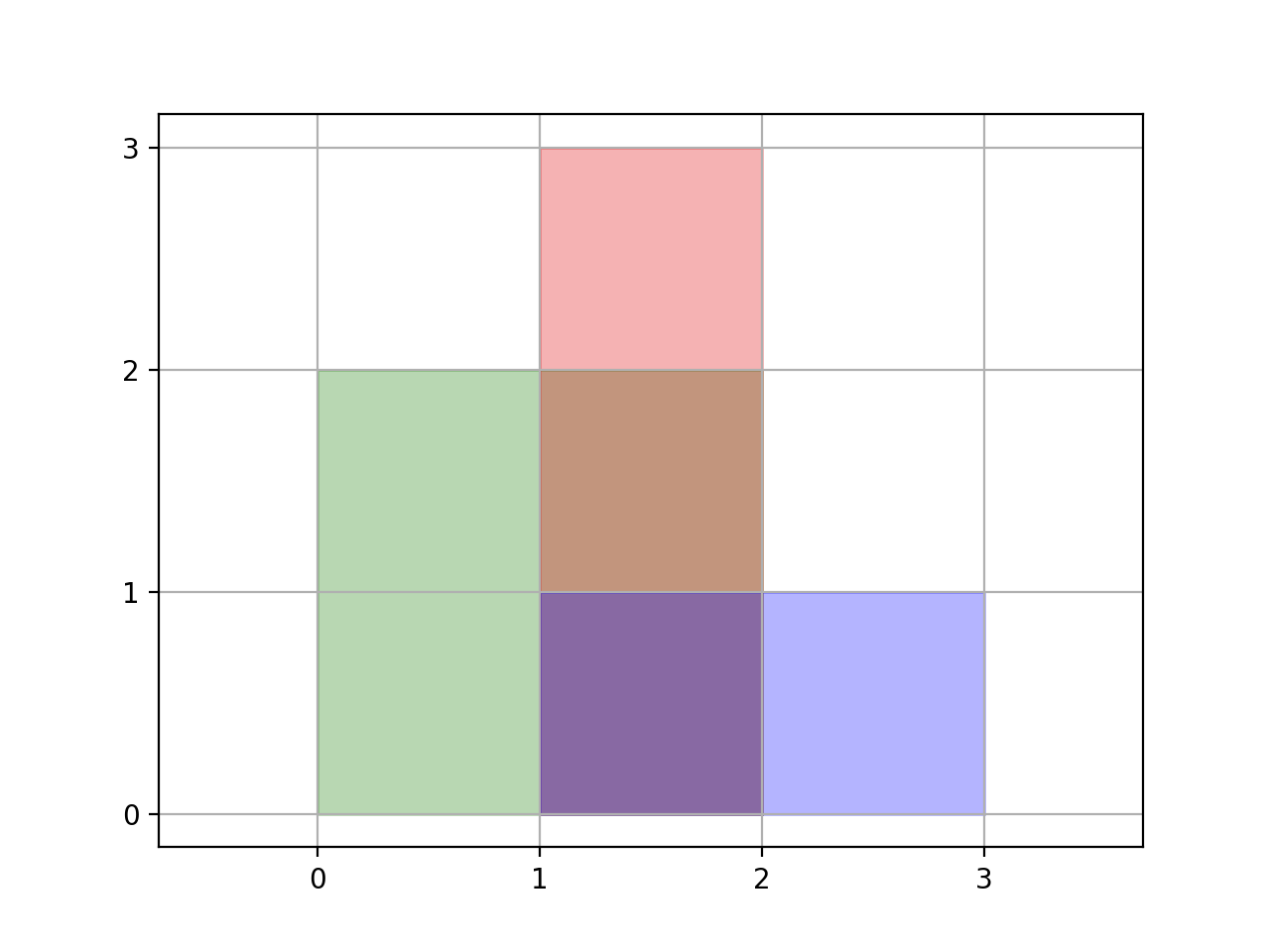
Input: rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]] Output: 6 Explanation: A total area of 6 is covered by all three rectangles, as illustrated in the picture. From (1,1) to (2,2), the green and red rectangles overlap. From (1,0) to (2,3), all three rectangles overlap.
Example 2:
Input: rectangles = [[0,0,1000000000,1000000000]] Output: 49 Explanation: The answer is 1018 modulo (109 + 7), which is 49.
Constraints:
1 <= rectangles.length <= 200rectanges[i].length == 40 <= xi1, yi1, xi2, yi2 <= 109xi1 <= xi2yi1 <= yi2- All rectangles have non zero area.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of the x and y coordinates for each rectangle?
- Can rectangles overlap, and if so, how should overlapping areas be handled?
- Can the input list of rectangles be empty or null?
- Should the result be an integer, or can it be a floating-point number to account for very small areas?
- Is the order of rectangles in the input significant, or should I treat them as an unordered set?
Brute Force Solution
Approach
The brute force method for finding the total area covered by overlapping rectangles involves checking every possible small area to see if it's covered by at least one rectangle. We essentially divide the entire space into very tiny squares and count how many of these squares are inside any of the rectangles.
Here's how the algorithm would work step-by-step:
- Imagine a very fine grid covering the entire space where the rectangles might be.
- For each tiny square in the grid, check if any of the rectangles overlap it.
- If a square is covered by at least one rectangle, mark it as covered.
- After checking every tiny square, count all the squares that are marked as covered.
- The total area is then approximately equal to the number of covered squares, assuming each square represents a very small unit of area. The finer the grid, the more accurate the area calculation.
Code Implementation
def rectangle_area_ii_brute_force(rectangles, grid_size=0.1):
min_x = float('inf')
min_y = float('inf')
max_x = float('-inf')
max_y = float('-inf')
for rectangle in rectangles:
x1, y1, x2, y2 = rectangle
min_x = min(min_x, x1)
min_x = min(min_x, x2)
min_y = min(min_y, y1)
min_y = min(min_y, y2)
max_x = max(max_x, x1)
max_x = max(max_x, x2)
max_y = max(max_y, y1)
max_y = max(max_y, y2)
total_area = 0
# Iterate over all possible squares within the bounding box.
for x in range(int(min_x * (1 / grid_size)), int(max_x * (1 / grid_size))):
for y in range(int(min_y * (1 / grid_size)), int(max_y * (1 / grid_size))):
square_x1 = x * grid_size
square_y1 = y * grid_size
square_x2 = (x + 1) * grid_size
square_y2 = (y + 1) * grid_size
is_covered = False
# Check if the current square is covered by any rectangle.
for rectangle in rectangles:
rect_x1, rect_y1, rect_x2, rect_y2 = rectangle
if (square_x1 < rect_x2 and square_x2 > rect_x1 and
square_y1 < rect_y2 and square_y2 > rect_y1):
# The current square is covered by at least one rectangle.
is_covered = True
break
if is_covered:
# Increase the total area if the square is covered.
total_area += grid_size * grid_size
return total_areaBig(O) Analysis
Optimal Solution
Approach
The challenge is to calculate the total area covered by a set of overlapping rectangles. The key is to avoid double-counting areas where rectangles overlap by smartly sweeping a line across the rectangles and tracking the covered intervals. This gives us a much faster calculation than brute-force.
Here's how the algorithm would work step-by-step:
- Imagine a vertical line sweeping from left to right across all the rectangles.
- As the line moves, it encounters the left or right edges of rectangles. These are important events.
- At each event (rectangle edge), note the height intervals currently covered by rectangles.
- To do this, keep track of the vertical intervals along the sweeping line where at least one rectangle is present.
- Multiply the length of the sweeping line's movement (the distance between adjacent rectangle edge x-coordinates) by the total height currently covered by the active intervals.
- Add this area to a running total. This is because each step of the vertical sweeping line is effectively calculating the area of a very thin rectangle.
- Repeat this process for every change in vertical coverage as the line sweeps, and the final running total will be the area covered by all rectangles, accounting for overlaps.
Code Implementation
def rectangle_area_ii(rectangles):
MODULO = 10**9 + 7
events = []
for x1, y1, x2, y2 in rectangles:
events.append((x1, y1, y2, 1)) # 1 for start
events.append((x2, y1, y2, -1)) # -1 for end
events.sort()
active_intervals = []
previous_x = 0
total_area = 0
for x, y1, y2, change in events:
# Calculate width of the current sweep
width = x - previous_x
# Calculate the covered height by active intervals
covered_height = 0
if active_intervals:
active_intervals.sort()
current_end = active_intervals[0][0]
total_covered = 0
for start, end in active_intervals:
current_end = max(current_end, start)
total_covered = max(total_covered, min(end, current_end) - current_end if end > current_end else 0)
current_end = max(current_end, end)
last_y = -1
for start, end in active_intervals:
if start > last_y:
covered_height += end - start
else:
covered_height += max(0, end - last_y)
last_y = max(last_y, end)
covered_height = 0
last_y = -1
for start, end in active_intervals:
start = max(start, last_y)
if start < end:
covered_height += end - start
last_y = end
# Accumulate the area
total_area = (total_area + width * covered_height) % MODULO
# Update the active intervals
if change == 1:
active_intervals.append((y1, y2))
else:
active_intervals.remove((y1, y2))
previous_x = x
return total_areaBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input rectangle list | Return 0 immediately as there are no rectangles to calculate area for. |
| Single rectangle in the input list | Return the area of that single rectangle without any further processing. |
| Maximum number of rectangles (e.g., 200) with large coordinates | Ensure the data structures (like events or active intervals) are appropriately sized to handle the input and avoid memory issues, and that the sweep line algorithm's time complexity is efficient enough. |
| Rectangles with negative coordinates | Shift all coordinates to be non-negative by finding the minimum x and y values and subtracting them from all coordinates, then proceed with the standard algorithm. |
| Overlapping rectangles completely covering the same area | The union of overlapping areas will be correctly calculated by the sweep line algorithm, preventing double-counting of area. |
| Rectangles with very small areas (close to zero) or zero width/height | Use appropriate data types (e.g., double) and consider a tolerance value when comparing floating-point numbers to avoid precision errors. |
| Integer overflow during area calculation (large coordinates) | Use a 64-bit integer type (long) to store intermediate and final area calculations to prevent overflow, and calculate modulo at each step if necessary. |
| Floating point precision issues when subtracting or comparing coordinates | Use a small epsilon value (e.g., 1e-9) when comparing floating-point numbers and consider using integers if coordinate ranges are suitable after scaling. |