Redundant Connection
MediumIn this problem, a tree is an undirected graph that is connected and has no cycles.
You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.
Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.
Example 1:
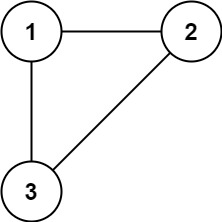
Input: edges = [[1,2],[1,3],[2,3]] Output: [2,3]
Example 2:
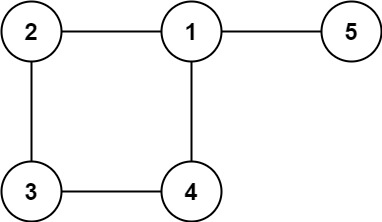
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]] Output: [1,4]
Constraints:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ai < bi <= edges.lengthai != bi- There are no repeated edges.
- The given graph is connected.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the graph? Can they be negative or zero?
- If there are multiple redundant connections, should I return the one that appears last in the input array?
- Will the input graph always be fully connected (i.e., will removing the redundant edge disconnect the graph)?
- Is the input guaranteed to represent a valid graph structure (e.g., no self-loops or parallel edges besides the redundant one)?
- If the input is empty or null, what should I return?
Brute Force Solution
Approach
The core idea is to go through all possibilities. We remove each connection one by one and check if removing it creates a graph that's still fully connected. If it is, then that connection is the redundant one.
Here's how the algorithm would work step-by-step:
- Start with the last connection in the list.
- Temporarily remove that connection from the graph.
- Check if the graph is still fully connected after removing the connection. This means can you still reach every part of the graph from any starting point.
- If the graph is no longer fully connected, put the connection back.
- Move to the next-to-last connection in the list and repeat steps two through four.
- Keep doing this, moving backwards through the list of connections, until you find a connection that, when removed, leaves the graph fully connected.
- The first such connection that you find (going backwards through the list) is the redundant connection you're looking for.
Code Implementation
def find_redundant_connection(edges):
number_of_edges = len(edges)
for edge_to_remove_index in range(number_of_edges - 1, -1, -1):
# Create a copy of the edges to avoid modifying the original
temp_edges = edges[:edge_to_remove_index] + edges[edge_to_remove_index + 1:]
number_of_nodes = len(edges) + 1
adjacent_list = [[] for _ in range(number_of_nodes)]
for node1, node2 in temp_edges:
adjacent_list[node1].append(node2)
adjacent_list[node2].append(node1)
# Check connectivity using Depth First Search
visited = [False] * number_of_nodes
def depth_first_search(node):
visited[node] = True
for neighbor in adjacent_list[node]:
if not visited[neighbor]:
depth_first_search(neighbor)
# Start DFS from node 1
depth_first_search(1)
# Check if all nodes are visited
is_connected = all(visited[1:])
if is_connected:
# Found the redundant edge
return edges[edge_to_remove_index]
return NoneBig(O) Analysis
Optimal Solution
Approach
We can use a structure that keeps track of different groups or sets, where each item in the problem initially starts in its own group. When we encounter a line, we check if the items connected by that line are already in the same group. If they are, that line is redundant and can be removed.
Here's how the algorithm would work step-by-step:
- Start by considering each item as being in its own separate group.
- Go through the lines one by one.
- For each line, check if the two items connected by that line are already in the same group.
- If the two items are already in the same group, it means adding this line would create a cycle and is therefore redundant; save this line.
- If the two items are in different groups, merge their groups together to show they are now connected.
- Continue this process until all lines have been examined.
- The last redundant line you saved is the one you should return.
Code Implementation
def find_redundant_connection(edges):
number_of_nodes = len(edges)
parent = list(range(number_of_nodes + 1))
def find(node):
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
def union(node_one, node_two):
root_one = find(node_one)
root_two = find(node_two)
if root_one != root_two:
parent[root_one] = root_two
return True
return False
redundant_edge = None
for edge in edges:
node_one, node_two = edge[0], edge[1]
# If nodes are already in same set,
# then this edge is redundant.
if not union(node_one, node_two):
redundant_edge = edge
# Return the last redundant edge found.
return redundant_edgeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty input graph (no edges) | Return an empty list or null since there's no redundant connection. |
| Graph with only two nodes and one edge | Return the given edge as there can be no cycle with only one edge. |
| Graph with no redundant connection (already a tree) | If the algorithm doesn't find a cycle, return an empty list or null indicating no redundant edge. |
| Large number of nodes, approaching memory limits | Ensure the chosen data structure (e.g., Disjoint Set Union) scales well and doesn't cause memory overflow by considering alternative representations for very large graphs. |
| Nodes are not numbered sequentially starting from 1 | Map node names to sequential indices within the algorithm, then reverse the mapping in the result. |
| Multiple possible redundant edges; which one to return? | The problem statement defines the order of edges in the input determines which edge is redundant. |
| Integer overflow when calculating union or find operations if node values are excessively large | Consider using a different data type (e.g., long) to store node values or implement a hash-based solution if node values are arbitrarily large and sparse. |
| Input contains self-loops (edge from a node to itself) | The Disjoint Set Union solution handles this case correctly as the find operation will detect it as a cycle. |