Redundant Connection II
Redundant Connection II #1915 Most Asked
HardIn this problem, a rooted tree is a directed graph such that, there is exactly one node (the root) for which all other nodes are descendants of this node, plus every node has exactly one parent, except for the root node which has no parents.
The given input is a directed graph that started as a rooted tree with n nodes (with distinct values from 1 to n), with one additional directed edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed.
The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [ui, vi] that represents a directed edge connecting nodes ui and vi, where ui is a parent of child vi.
Return an edge that can be removed so that the resulting graph is a rooted tree of n nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array.
Example 1:
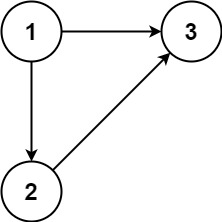
Input: edges = [[1,2],[1,3],[2,3]] Output: [2,3]
Example 2:

Input: edges = [[1,2],[2,3],[3,4],[4,1],[1,5]] Output: [4,1]
Constraints:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ui, vi <= nui != vi
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- The addition of an edge can violate the rooted tree property in two ways: a node might get two parents, or a cycle could be formed. Can a single added edge cause both of these issues to occur at the same time?
- Regarding the tie-breaking rule to return the last edge in the input: if there are multiple edges that could each be removed to form a valid rooted tree, is the choice solely based on which of these valid edges appears latest in the input array?
- Is it guaranteed that the input graph is always formed from a valid rooted tree plus exactly one extra edge, and that a solution can always be found by removing a single edge?
- Are all nodes from 1 to `n` guaranteed to be present in the `edges` list, or could there be isolated nodes that don't appear in any edge?
- After removing the redundant edge to form a valid rooted tree, can the root of this new tree be a different node than the root of the original tree before the extra edge was added?
Brute Force Solution
Approach
Imagine you have a set of one-way roads between cities, but one extra road messes things up by either creating a circular route or making one city have two incoming roads. The brute force approach is to try removing each road, one by one, and checking if the remaining road system is valid.
Here's how the algorithm would work step-by-step:
- Take the entire list of connections and pick one to test. Let's start with the last one in the list and work our way backwards.
- Temporarily ignore that single connection you picked.
- Now, look at the map formed by all the other connections.
- Check if this new map is a 'valid tree'. A valid tree means every city can be reached from a single 'capital' city, and no city has more than one road leading directly into it.
- To do this, we first count how many roads lead into each city. If any city has two, it's not a valid tree.
- We also trace the paths from each city to see if there are any loops, like a path from city A to B, B to C, and C back to A. A valid tree has no loops.
- Finally, we confirm that all cities are part of one single connected system.
- If the map with the removed connection passes all these checks, then the connection we ignored is the right one to remove. Since we are checking from the end of the list backwards, the first one we find that works is our answer.
Code Implementation
def find_redundant_directed_connection(connections):
number_of_nodes = len(connections)
def is_valid_tree(nodes_count, candidate_connections):
parent_of_node = {}
adjacency_list = {node_identifier: [] for node_identifier in range(1, nodes_count + 1)}
for source_node, destination_node in candidate_connections:
# A node with two parents directly violates the core definition of a tree structure.
if destination_node in parent_of_node:
return False
parent_of_node[destination_node] = source_node
adjacency_list[source_node].append(destination_node)
root_candidate = -1
number_of_roots = 0
for node_identifier in range(1, nodes_count + 1):
if node_identifier not in parent_of_node:
number_of_roots += 1
root_candidate = node_identifier
# For a structure to be a single rooted tree, there must be exactly one starting point.
if number_of_roots != 1:
return False
visited_nodes = {root_candidate}
nodes_to_visit_stack = [root_candidate]
while nodes_to_visit_stack:
current_node = nodes_to_visit_stack.pop()
for neighbor_node in adjacency_list[current_node]:
if neighbor_node not in visited_nodes:
visited_nodes.add(neighbor_node)
nodes_to_visit_stack.append(neighbor_node)
# If the traversal from the root can't reach every node, it's not one single connected tree.
return len(visited_nodes) == nodes_count
for connection_index in range(number_of_nodes - 1, -1, -1):
temporary_connections = connections[:connection_index] + connections[connection_index + 1:]
if is_valid_tree(number_of_nodes, temporary_connections):
return connections[connection_index]
return []Big(O) Analysis
Optimal Solution
Approach
The structure described is almost a perfect tree, but one extra connection messes things up. This creates one of two problems: a circular path, or a destination with two sources. Our strategy is to first check for the 'two sources' problem, as it gives us the best clues to find and remove the single incorrect connection.
Here's how the algorithm would work step-by-step:
- First, we perform a quick check through all the connections to see if any destination has two different sources pointing to it. A destination having two sources is a clear problem.
- If no destination has two sources, the problem must be a simple circular path. We can find this by adding connections one by one until adding one would form a closed loop. That connection is the one to remove.
- If we do find a destination with two sources, we have two 'suspect' connections that could be the problem. Let's call them Suspect A and Suspect B, where Suspect B is the one that appears later in the given list.
- To figure out which suspect is the real culprit, we conduct a test. We temporarily assume Suspect B is the incorrect one and set it aside.
- With Suspect B out of the picture, we check if all the remaining connections (including Suspect A) form a valid, loop-free structure.
- If the remaining connections are perfectly fine and have no loops, it confirms our assumption was correct. Suspect B is the connection we need to remove.
- However, if the remaining connections still contain a loop even after we set Suspect B aside, it means the loop must involve Suspect A. In this case, removing Suspect A is the only way to fix both the loop and the 'two sources' problem at the same time, so Suspect A is the answer.
Code Implementation
class Solution:
def findRedundantDirectedConnection(self, edges):
class DSU:
def __init__(self, number_of_elements):
self.parent_array = list(range(number_of_elements + 1))
def find(self, node):
if self.parent_array[node] == node:
return node
self.parent_array[node] = self.find(self.parent_array[node])
return self.parent_array[node]
def union(self, first_node, second_node):
root_of_first = self.find(first_node)
root_of_second = self.find(second_node)
if root_of_first != root_of_second:
self.parent_array[root_of_second] = root_of_first
return True
return False
number_of_nodes = len(edges)
child_to_parent_map = {}
first_candidate_edge = None
second_candidate_edge = None
for current_edge in edges:
parent_node, child_node = current_edge
if child_node in child_to_parent_map:
# A node with two parents is found, identifying two candidate edges for removal.
first_candidate_edge = [child_to_parent_map[child_node], child_node]
second_candidate_edge = current_edge
break
child_to_parent_map[child_node] = parent_node
if not first_candidate_edge:
# If no node has two parents, the problem is to find the first edge that forms a cycle.
union_find_structure = DSU(number_of_nodes)
for current_edge in edges:
parent_node, child_node = current_edge
if not union_find_structure.union(parent_node, child_node):
return current_edge
union_find_structure = DSU(number_of_nodes)
for current_edge in edges:
if current_edge == second_candidate_edge:
# Temporarily ignore the second candidate to check if removing it resolves all issues.
continue
parent_node, child_node = current_edge
if not union_find_structure.union(parent_node, child_node):
# A cycle exists without the second candidate, so the first candidate must be the answer.
return first_candidate_edge
return second_candidate_edgeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| The added edge creates a cycle, but no node ends up with two parents. | The solution uses a Union-Find data structure to iterate through edges and identifies the last one that connects two nodes already in the same component. |
| The added edge gives a node a second parent, but this does not create a cycle. | The algorithm identifies the two potential edges and correctly selects the one that appears later, as removing it is tested first and results in a valid tree. |
| The added edge creates both a cycle and a node with two parents simultaneously. | The solution identifies that the edge to be removed is the one of the two parent-creating edges that also participates in the cycle. |
| Removing a candidate edge for a two-parent node results in a disconnected graph (a forest). | The solution validates not only for cycles but also ensures the graph remains a single connected component to correctly identify the redundant edge. |
| Multiple edges are valid candidates for removal. | The solution strictly follows the problem's tie-breaking rule by returning the candidate edge that appears last in the input array. |
| Input graph is large, approaching the maximum size of n=1000. | The solution uses an efficient Union-Find approach, ensuring a near-linear time complexity that scales effectively for large inputs. |
| Node values are 1-indexed (from 1 to n), a common source of off-by-one errors. | The implementation must handle array access carefully, typically by using arrays of size n+1 to map node values directly to indices. |
| The root of the original tree is involved in the structural issue, such as becoming part of a cycle. | The algorithm is general and does not need special logic, as its cycle detection and parent tracking mechanisms handle all nodes uniformly. |