Reorder Routes to Make All Paths Lead to the City Zero
MediumThere are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.
This year, there will be a big event in the capital (city 0), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.
It's guaranteed that each city can reach city 0 after reorder.
Example 1:
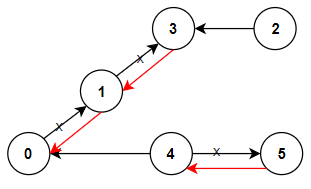
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]] Output: 3 Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
Example 2:

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]] Output: 2 Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
Example 3:
Input: n = 3, connections = [[1,0],[2,0]] Output: 0
Constraints:
2 <= n <= 5 * 104connections.length == n - 1connections[i].length == 20 <= ai, bi <= n - 1ai != bi
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the number of cities *n* and the number of connections (elements in the *connections* array)?
- Can there be multiple connections between the same two cities, or self-loops (a connection from a city to itself)?
- Is the input guaranteed to represent a connected graph, meaning there's a path between any two cities?
- If there is no way to reorder the routes such that all paths lead to city 0, what should I return?
- Does the order of elements within each connection (e.g., [0, 1] vs. [1, 0]) matter in the input? If the problem statement said paths lead *from* zero, the order would not matter.
Brute Force Solution
Approach
The brute force strategy involves exploring every possible combination of reordering the routes to see which configuration requires the fewest changes to make all paths lead to city zero. We'll systematically try flipping each route's direction and count how many flips are needed to achieve the desired outcome. We repeat this process until we've checked all possibilities.
Here's how the algorithm would work step-by-step:
- Start by considering all the routes in their original direction.
- Check if, with the routes in this original direction, all paths lead to city zero. If so, we need zero flips and we're done.
- If not, consider flipping the direction of the first route and checking if now all paths lead to city zero. Keep track of the number of flips.
- Next, try flipping the direction of the second route (while keeping the first route in its original direction) and check again.
- Repeat this for every route, flipping them one at a time and testing if all paths now lead to city zero.
- Now consider flipping two routes at a time in every possible combination, checking for the required paths after each combination.
- Continue this process, flipping three routes, four routes, and so on, until you've tried flipping all the routes.
- For each combination of flipped routes that result in all paths leading to city zero, record the number of flips.
- Finally, from all the recorded flip counts, choose the smallest number. That smallest number is the minimum number of routes we need to change.
Code Implementation
def reorder_routes_brute_force(number_of_cities, connections):
minimum_reorders = float('inf')
for i in range(2**len(connections)):
reorders_needed = 0
modified_connections = []
# Construct modified connections based on the bitmask.
for j in range(len(connections)):
if (i >> j) & 1:
modified_connections.append((connections[j][1], connections[j][0]))
reorders_needed += 1
else:
modified_connections.append(connections[j])
# Check if all paths lead to city zero
if can_reach_zero(number_of_cities, modified_connections):
minimum_reorders = min(minimum_reorders, reorders_needed)
return minimum_reorders
def can_reach_zero(number_of_cities, connections):
graph = [[] for _ in range(number_of_cities)]
for start, end in connections:
graph[start].append(end)
visited = [False] * number_of_cities
queue = [0]
visited[0] = True
while queue:
current_city = queue.pop(0)
for neighbor in graph[current_city]:
if not visited[neighbor]:
visited[neighbor] = True
queue.append(neighbor)
# Ensure all cities can reach zero
return all(visited)
# This is the main method
def min_reorder(number_of_cities, connections):
#The brute force method will try all combinations
return reorder_routes_brute_force(number_of_cities, connections)Big(O) Analysis
Optimal Solution
Approach
The core idea is to explore the city network systematically, starting from city zero. We want to count only the roads that are initially pointing away from city zero, as we need to flip those to make them point towards zero.
Here's how the algorithm would work step-by-step:
- Begin at city zero, because this is our destination for all paths.
- As you visit each city, remember which city you came from to avoid going in circles.
- For each road connected to the current city, check if it points away from city zero. If it does, that means we need to reverse it, so count it.
- Continue exploring the network city by city, always starting from zero and making sure to reverse only the roads initially pointing away from the destination.
- By the end of your exploration, the total count is the minimum number of roads you need to reverse.
Code Implementation
def reorder_routes(number_of_cities, connections):
adjacent_list = [[] for _ in range(number_of_cities)]
for start, end in connections:
adjacent_list[start].append((end, 1))
adjacent_list[end].append((start, 0))
number_of_reversals = 0
visited = [False] * number_of_cities
def depth_first_search(city):
nonlocal number_of_reversals
visited[city] = True
for neighbor, direction in adjacent_list[city]:
if not visited[neighbor]:
# Prioritize moving towards zero.
if direction == 1:
# Increment if the road points away from zero.
number_of_reversals += 1
depth_first_search(neighbor)
# Start the search from city zero.
depth_first_search(0)
# Return the total count of reversed roads.
return number_of_reversalsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty connections array | Return 0 as no reordering is needed since there are no routes. |
| n = 1 (single city, no connections) | Return 0 as there are no routes to reorder. |
| Maximum number of cities (n = 5 * 10^4) | Ensure the graph representation (adjacency list) is space-efficient and the traversal algorithm (BFS/DFS) handles large graphs without stack overflow. |
| Connections form a disconnected graph | The problem statement guarantees a connected graph; this case should not occur, but adding a check to identify and handle such graphs increases code robustness. |
| All connections already point towards city 0 | Return 0 as no reordering is needed. |
| All connections point away from city 0 (maximum reordering needed) | Algorithm correctly calculates the maximum reorderings required. |
| Cycle in the graph | The BFS/DFS algorithm with a visited set correctly handles cycles, preventing infinite loops and ensuring each edge is visited only once. |
| Input contains duplicate connections. | The graph construction (adjacency list) handles duplicate connections correctly by only storing the connection once during graph building. |