Reshape the Matrix #4 Most Asked
EasyIn MATLAB, there is a handy function called reshape which can reshape an m x n matrix into a new one with a different size r x c keeping its original data.
You are given an m x n matrix mat and two integers r and c representing the number of rows and the number of columns of the wanted reshaped matrix.
The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the reshape operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
Example 1:
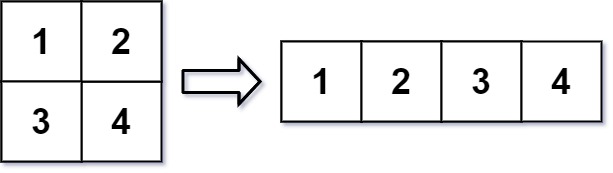
Input: mat = [[1,2],[3,4]], r = 1, c = 4 Output: [[1,2,3,4]]
Example 2:
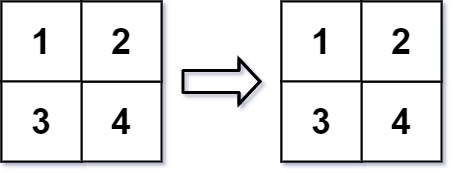
Input: mat = [[1,2],[3,4]], r = 2, c = 4 Output: [[1,2],[3,4]]
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 100-1000 <= mat[i][j] <= 10001 <= r, c <= 300
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- If it's impossible to reshape the matrix with the given dimensions (r, c), what should I return?
- Can the input matrix be empty or null? What about if r or c are zero?
- Are the values of 'r' and 'c' guaranteed to be non-negative integers?
- Does the number of elements in the original matrix always equal r * c?
- What data type will the elements of the matrix be (e.g., integers, floats)? Will there be any constraints on the range of values within the matrix?
Brute Force Solution
Approach
We're given a grid of numbers and want to reorganize it into a new grid with different dimensions. The brute force method essentially flattens the original grid into a single line, and then tries to reconstruct the new grid by filling it row by row from this line.
Here's how the algorithm would work step-by-step:
- First, imagine all the numbers from the original grid are laid out in a single row, one after the other.
- Next, start building the new grid row by row.
- Take the first chunk of numbers from our single row and put them into the first row of the new grid, making sure you take the exact number of numbers needed to fill that row.
- Then, take the next chunk of numbers and put them into the second row of the new grid, again making sure to take the right amount of numbers.
- Keep doing this until the new grid is completely filled. If you run out of numbers before the new grid is full, or if you have numbers left over after filling the grid, then the reshaping isn't possible.
Code Implementation
def matrixReshape(matrix, rows, cols): originalRows = len(matrix)
originalCols = len(matrix[0]) if originalRows > 0 else 0
# Check if reshaping is possible
if originalRows * originalCols != rows * cols:
return matrix
flattenedMatrix = []
for row in matrix:
for element in row:
flattenedMatrix.append(element)
reshapedMatrix = []
index = 0
# Build the new matrix row by row
for rowIndex in range(rows):
newRow = []
for colIndex in range(cols):
newRow.append(flattenedMatrix[index])
index += 1
reshapedMatrix.append(newRow)
return reshapedMatrixBig(O) Analysis
Optimal Solution
Approach
The goal is to take all the numbers from the original arrangement and put them into a new one with a different shape. The clever approach sees the original arrangement as one long continuous list of numbers and then repackages those numbers into the desired new shape.
Here's how the algorithm would work step-by-step:
- Imagine all the numbers from the original arrangement are laid out in a single line, one after another.
- Now, think about building the new arrangement row by row.
- Take the first group of numbers from the line and put them into the first row of the new arrangement.
- Continue taking groups of numbers from the line and filling the rows of the new arrangement until it's complete.
- If the requested shape can’t be formed using all the original numbers, report that it can’t be done. Otherwise, return the new arrangement.
Code Implementation
def matrixReshape(matrix, target_row_count, target_column_count):
original_row_count = len(matrix)
original_column_count = len(matrix[0])
# Check if reshaping is possible.
if original_row_count * original_column_count != target_row_count * target_column_count:
return matrix
reshaped_matrix = [([0] * target_column_count) for _ in range(target_row_count)]
row_index = 0
column_index = 0
# Iterate through the original matrix and populate the reshaped one.
for i in range(original_row_count):
for j in range(original_column_count):
reshaped_matrix[row_index][column_index] = matrix[i][j]
column_index += 1
# Move to the next row if the current row is filled.
if column_index == target_column_count:
row_index += 1
column_index = 0
return reshaped_matrixBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Input matrix is null or empty | Return the original matrix if it is null or empty as there's nothing to reshape. |
| Target row or column is zero | Return the original matrix, since a row or column of size zero is not valid to reshape to. |
| Target row or column are negative | Return the original matrix since row and column size cannot be negative. |
| The product of original matrix dimensions doesn't equal the product of target dimensions | Return the original matrix because reshaping is impossible if total element counts are different. |
| Original matrix has dimensions (1, 1) and target has different dimensions | Reshape the single element matrix correctly to the new (1, 1) matrix or return the original if the target is not (1,1). |
| Large matrix dimensions that could potentially cause integer overflow when calculating the total number of elements | Use a data type that can accommodate larger numbers or check for overflow before multiplication. |
| Target row or column values are extremely large | Consider the feasibility of creating such a large matrix with the available memory and handle memory exceptions appropriately. |
| Original matrix contains extreme boundary values (min/max int) | The algorithm is not affected by the boundary values, it simply needs to be copied to the right place |