Reverse Odd Levels of Binary Tree

Medium

Asked by:

14 views

Topics:

TreesRecursion

Given the root of a perfect binary tree, reverse the node values at each odd level of the tree.

For example, suppose the node values at level 3 are [2,1,3,4,7,11,29,18], then it should become [18,29,11,7,4,3,1,2].

Return the root of the reversed tree.

A binary tree is perfect if all parent nodes have two children and all leaves are on the same level.

The level of a node is the number of edges along the path between it and the root node.

Example 1:

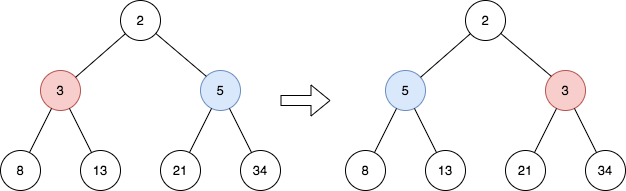
Input: root = [2,3,5,8,13,21,34]
Output: [2,5,3,8,13,21,34]
Explanation: 
The tree has only one odd level.
The nodes at level 1 are 3, 5 respectively, which are reversed and become 5, 3.

Example 2:

Input: root = [7,13,11]
Output: [7,11,13]
Explanation: 
The nodes at level 1 are 13, 11, which are reversed and become 11, 13.

Example 3:

Input: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
Output: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
Explanation: 
The odd levels have non-zero values.
The nodes at level 1 were 1, 2, and are 2, 1 after the reversal.
The nodes at level 3 were 1, 1, 1, 1, 2, 2, 2, 2, and are 2, 2, 2, 2, 1, 1, 1, 1 after the reversal.

Constraints:

The number of nodes in the tree is in the range [1, 2¹⁴].
0 <= Node.val <= 10⁵
root is a perfect binary tree.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range of values that the nodes in the tree can hold?
Can the binary tree be empty or contain only a single node?
Is the root level considered level 0 or level 1? How is level defined?
If a level has only one node, should I still reverse it?
Is the binary tree guaranteed to be a complete binary tree or a full binary tree? Or can it be any arbitrary binary tree?

Brute Force Solution

Approach

The brute force method for reversing odd levels in a binary tree involves examining every possible way to modify the tree. We achieve this by generating all permutations of nodes on the odd levels and checking if any of them fulfill the reverse requirement. This approach is exhaustive, ensuring we explore all solutions.

Here's how the algorithm would work step-by-step:

First, get a list of all nodes at each level of the tree.
Then, identify the levels that are considered 'odd'.
For each odd level, create a list of all the different ways you could rearrange the order of the nodes at that level. Think of it like shuffling a deck of cards.
For each of those rearrangements, make a new copy of the entire tree.
In that new copy, change the order of the nodes on the odd level to match the rearrangement you are testing.
After changing the order, check if this new tree satisfies the rule that the odd levels must be reversed. If it does, then you have found a possible solution.
Repeat this process for every possible rearrangement on every odd level.
If you find multiple valid trees that satisfy the rule, you can return any one of them since the question doesn't specify how to select among multiple solutions.

Code Implementation

from collections import deque
from itertools import permutations
import copy

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def reverse_odd_levels_brute_force(root):
    if not root:
        return None

    # 1. Get nodes at each level
    levels = []
    queue = deque([root])
    while queue:
        level_size = len(queue)
        current_level = []
        for _ in range(level_size):
            node = queue.popleft()
            current_level.append(node)
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        levels.append(current_level)

    # 2. Identify odd levels (0-indexed)
    odd_levels = [levels[i] for i in range(1, len(levels), 2)]

    # 3. Iterate through permutations of nodes in odd levels
    for i, odd_level in enumerate(odd_levels):
        original_nodes = [node.val for node in odd_level]

        # 4. Generate all permutations for current odd level
        for permutation in permutations(original_nodes):
            
            # 5. Create a copy of the tree
            new_root = copy.deepcopy(root)
            new_levels = []
            queue = deque([new_root])
            while queue:
                level_size = len(queue)
                current_level = []
                for _ in range(level_size):
                    node = queue.popleft()
                    current_level.append(node)
                    if node.left:
                        queue.append(node.left)
                    if node.right:
                        queue.append(node.right)
                new_levels.append(current_level)

            #6. Change the node values to match permutation
            new_odd_level = new_levels[2 * i + 1] #Convert odd levels back to index in levels

            # Assign the permutation values to the nodes
            for index, node in enumerate(new_odd_level):
                node.val = permutation[index]

            # 7. Check if the tree satisfies the reverse condition

            is_valid = True
            new_levels_check = []
            queue = deque([new_root])
            while queue:
                level_size = len(queue)
                current_level = []
                for _ in range(level_size):
                    node = queue.popleft()
                    current_level.append(node)
                    if node.left:
                        queue.append(node.left)
                    if node.right:
                        queue.append(node.right)
                new_levels_check.append(current_level)

            for level_index in range(1, len(new_levels_check), 2):
                nodes_values = [node.val for node in new_levels_check[level_index]]
                if nodes_values != list(reversed(nodes_values)):
                    is_valid = False
                    break

            #8. Return if the tree is valid
            if is_valid:
                return new_root #Return as soon as possible

    return root #If no valid tree is found, return the original

Big(O) Analysis

Time Complexity

O(N! * M) – Let N be the maximum number of nodes on an odd level and M be the total number of nodes in the tree. For each odd level, we generate all possible permutations of the nodes, which takes O(N!) time per level. Generating a new copy of the tree for each permutation takes O(M) time, since we need to visit and copy each node. We perform this permutation and copying for each odd level of the tree. The number of levels is at most log(M), however since we do not know the number of odd levels in advance, and the permutation cost dominates, the overall time complexity is approximately O(N! * M), considering the maximum number of permutations for any odd level.

Space Complexity

O(N!) – The algorithm generates all permutations of nodes at each odd level. In the worst case, an odd level might contain close to N/2 nodes, where N is the total number of nodes in the tree. Generating all permutations of these nodes requires storing (N/2)! permutations. Furthermore, for each permutation, a new copy of the entire tree is created, requiring O(N) space. Combining these factors, the space complexity is dominated by the permutation generation, leading to a space complexity of O(N!).

Optimal Solution

Approach

The key is to process the tree level by level, swapping nodes at odd levels directly without extra space. We use a helper function to efficiently swap nodes within each odd level.

Here's how the algorithm would work step-by-step:

Start by checking if the tree is empty. If it is, there's nothing to do.
Create a function that helps swap the values of two nodes that are symmetric to each other at an odd level.
Start processing from the root, considering the level number (starting from 0).
If the current level is odd, use the helper function to swap the node values on the left and the node values on the right.
Move down to the next level and recursively apply the same process to the left and right children.
The recursion stops when we reach the bottom of the tree or when there are no more odd levels to reverse.

Code Implementation

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def reverseOddLevels(self, root: TreeNode) -> TreeNode:
        if not root:
            return root

        def swap_nodes(node_one, node_two, level):
            if not node_one or not node_two:
                return

            # Swap values only at odd levels
            if level % 2 != 0:
                node_one.val, node_two.val = node_two.val, node_one.val

        def reverse_tree(node_left, node_right, level):
            if not node_left or not node_right:
                return

            swap_nodes(node_left, node_right, level)

            # Move down to the next level recursively
            reverse_tree(node_left.left, node_right.right, level + 1)
            reverse_tree(node_left.right, node_right.left, level + 1)

        # Begin the recursive reversal process
        reverse_tree(root.left, root.right, 1)

        return root

Big(O) Analysis

Time Complexity

O(n) – The algorithm visits each node of the binary tree exactly once. The swapping operation at each odd level involves a constant number of operations for each pair of nodes at that level. Since each node is visited and potentially swapped only once during the level-order traversal, the overall time complexity is directly proportional to the number of nodes in the tree, which is n. Therefore, the time complexity is O(n).

Space Complexity

O(H) – The primary space usage stems from the recursive calls. The algorithm processes the tree level by level, with recursive calls made for the left and right children at each node. The maximum depth of the recursion stack is equal to the height (H) of the binary tree. Therefore, the space complexity is proportional to the height of the tree, resulting in O(H) auxiliary space.

Edge Cases

Case	How to Handle
Null or empty tree	Return null immediately to handle empty input gracefully.
Tree with only a root node	Return the root node as is since there are no odd levels to reverse.
Tree with only two levels	Reverse the second level (level 1) by swapping the left and right children of the root if they exist.
Perfectly balanced tree with a large number of nodes	Ensure that the space complexity of the solution remains within acceptable limits, especially if using a level-order traversal with a queue or recursion with a call stack.
Skewed tree (e.g., all nodes on the left side)	The level-order traversal and reversal logic should handle uneven distribution of nodes correctly.
Tree where all nodes at an odd level have the same value	The reversal algorithm should still execute correctly, effectively swapping identical values.
Integer overflow during value swapping (though unlikely in this problem context)	Ensure that the swap operation doesn't cause an integer overflow if the node values are close to the maximum or minimum integer values (should not occur with standard node values).
Tree with duplicate node values at odd levels	Reversal based on level order will function correctly regardless of duplicate values as it modifies node pointers not node values directly.

Null or empty tree

How to Handle:

Return null immediately to handle empty input gracefully.

Tree with only a root node

How to Handle:

Return the root node as is since there are no odd levels to reverse.

Tree with only two levels

How to Handle:

Reverse the second level (level 1) by swapping the left and right children of the root if they exist.

Perfectly balanced tree with a large number of nodes

How to Handle:

Ensure that the space complexity of the solution remains within acceptable limits, especially if using a level-order traversal with a queue or recursion with a call stack.

Skewed tree (e.g., all nodes on the left side)

How to Handle:

The level-order traversal and reversal logic should handle uneven distribution of nodes correctly.

Tree where all nodes at an odd level have the same value

How to Handle:

The reversal algorithm should still execute correctly, effectively swapping identical values.

Integer overflow during value swapping (though unlikely in this problem context)

How to Handle:

Ensure that the swap operation doesn't cause an integer overflow if the node values are close to the maximum or minimum integer values (should not occur with standard node values).

Tree with duplicate node values at odd levels

How to Handle:

Reversal based on level order will function correctly regardless of duplicate values as it modifies node pointers not node values directly.